晶态固体热容的经验定律和经典理论

在19世纪已发现了两个有关晶体热容的经验定律。一是元素的热容定律——杜隆—珀蒂定律：恒压下元素的原子摩尔热容为25J/（K·mol）。实际上，大部分元素的原子摩尔热容都接近该值，特别在高温时符合得更好。只是轻元素的原子摩尔热容与此值相差较大。另一个是化合物的热容定律——柯普定律：化合物分子热容等于构成此化合物各元素原子热容之和。

经典的热容理论可对此经验定律作如下解释。在固体中可以用谐振子代表每一个原子在一个自由度的振动。根据经典理论，能量按自由度均分，每一振动自由度平均动能是（1/2）kT（参照理想气体分子的平均动能），因为是谐振子，平均势能等于平均动能，故平均势能也为（1/2）kT。那么每一个自由度的平均能量为kT。一个原子有三个振动自由度，一个原子的平均能量为3kT。1mol固体中有N₀个原子，总能量为E=3N₀kT=3RT。这里N₀=6.023×10²³，为阿伏加德罗常数，T为热力学温度，k为玻耳兹曼常数，摩尔气体常数R=8.314J/（K·mol）。根据摩尔定容热容定义

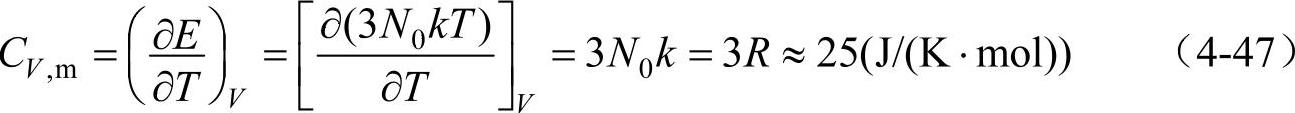
在简谐近似下，原子的振动是严格简谐的，不会发生热膨胀现象，因而定容的前提条件也成立。(www.xing528.com)

由式（4-47）可知，摩尔定容热容是与温度无关的常数，这就是杜隆—珀蒂定律。对于双原子的固态化合物，1mol中的原子数为2N₀，故摩尔定容热容为C_V，m=2×25J/（K·mol），三原子固态化合物的摩尔定容热容C_V，m=3×25J/（K·mol），余此类推。杜隆—珀蒂定律在高温时与实验结果是很符合的。但在低温时，摩尔定容热容的实验值并不是一个恒量。它随温度降低而减小，在接近0K时，摩尔定容热容值按T³的规律趋于零（绝缘体）或按AT+BT³的规律趋于零（金属）。如图4-8为Cu的C_V，m与T关系曲线（C_V，m值不是直接测量的，而是由测量C_p，m值换算来的），曲线可分三个区，每区的特点：Ⅰ区C_V，m∝T；Ⅱ区C_V，m∝T³；Ⅲ区逐渐过渡为平缓上升的直线。对于低温下摩尔定容热容减小的现象使经典理论遇到了困难，需要用量子理论来解释。

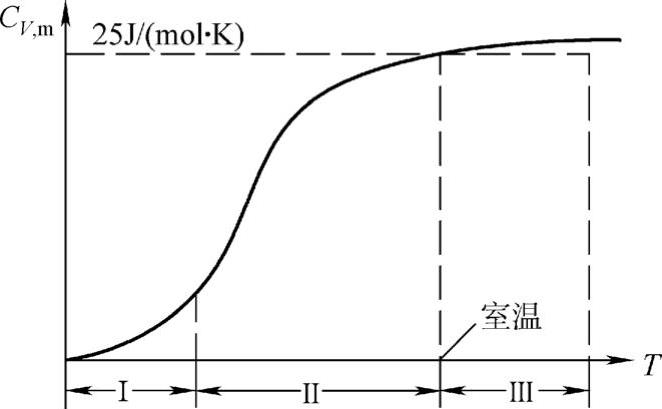
图4-8 Cu的C_V，m随T变化曲线