三维复式格子总能量优化分析

一维晶格振动量子化的主要方法和结论可以推广到三维晶格振动系统。对于含有N个原胞、每个原胞包括l个原子的三维晶格系统，其总能量E为

从式（4-39）可知，共有3lN种不同的振动模式（可以把一个原子空间振动分解为空间相互垂直的三个方向的振动），即3lN个不同的ω_j（q）值。ћω_j（q）是晶格振动能量的增减单位，也就是说晶格振动能量的增减必须是ћω_j（q）的整数倍，这种能量单元（或称能量量子）我们称为声子。

从声子概念出发，可以重新描述晶格振动问题。晶格振动是一种整体的激发形式，晶格振动时产生了声子，声子的能量是ћω_j（q），ω_j（q）是声子的频率，共有3lN种不同的频率模式。如果振动模从基态（能量为（1/2）ћω_j（q））激发到能量为[n_j（q）+1/2]ћω_j（q）的激发态，那么就产生了能量为ћω_j（q）的n_j（q）个声子。共有3支声学声子，3l-3支光学声子，根据声子偏振方向与波矢传播方向关系，又分纵向声子和横向声子。晶格振动系统可以转变为声子系统来研究，在简谐近似中，各振动模都是相互独立的，该系统为无相互作用的声子气系统。如果考虑非谐效应，那么声子和声子之间就存在相互作用。

下面我们分几个方面讨论一下声子问题。

①任意一谐振子其基态能量为ε₀=（1/2）ћω，具有激发能ε_n=（n+1/2）ћω的几率P_n是和exp（-ε_n/kT）成正比（k为玻耳兹曼常数），由于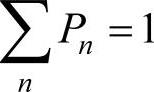，那么几率应由下式给出

式（4-40）中分子和分母的共同因子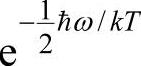被消去了。由于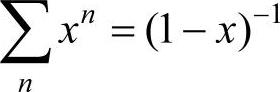，所以式（4-40）变为

由式（4-41）可以求出能量ε_n=（n+1/2）ћω振子的平均能量为(www.xing528.com)

利用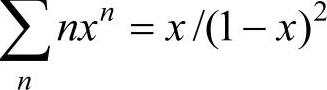，最后获得

又根据式（4-38），处于简振模ω_j（q）振子的平均能量应为

比较式（4-44）和式（4-43），有

从声子概念出发，n_j（q）是处于j、q态的声子平均数。因此由式（4-45）知，声子遵循玻色统计分布，声子是玻色子。

②在简谐近似中，声子气是无相互作用的声子构成的，声子是玻色子，因此晶格振动的每个状态能够被任何数目的不可区别的声子占据，声子数仅与晶格振动的能量值有关，即依赖于温度。在T=0K时，没有任何声子被激发。

正像我们可以把电磁波看成光子流一样，也可以把弹性波（在晶体中即为格波）看成声子流。和光子一样，声子是玻色子。