一维简单晶格振动的总能量计算

为简单起见，以一维单原子晶体振动的量子化为例，引出声子概念，然后推广到三维晶格的情况。

一维单原子链（参照图4-1。N个原子，原子质量为m，原子间距为a，恢复力常数为β），在简谐近似下，只考虑最近邻相互作用，那么总势能U为

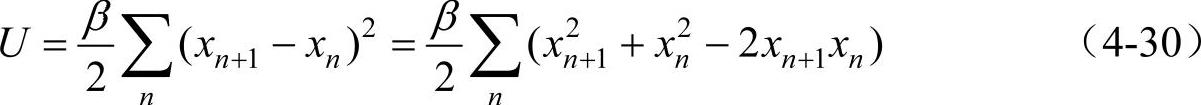
总动能T为

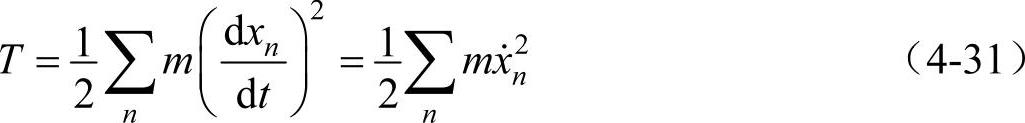
系统的总能量H为（即哈密顿量）

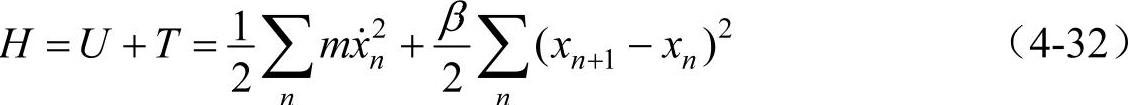
势能式（4-30）中包括了交叉项，通过坐标变换使交叉项消除。

运动方程式（4-3）的特解为式（4-4），即x_n=Aeⁱ（qna-ωt），一般解应为特解的线性组合，为

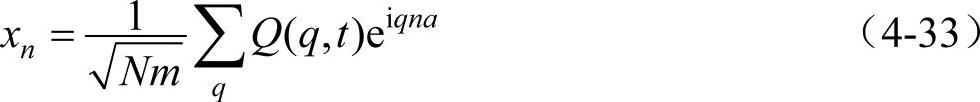
在式（4-33）中，式（4-32）的时间因子和振幅都包含在系数Q（q，t）中，而且质量因子也分离出来。式（4-33）实际上是代表x_n（t）在q空间的傅里叶展开式。

式（4-33）中的e^iqna，实际上代表一些独立的模式（q可取正值或负值，代表前进或后退简谐波），e^iqna具有正交性。根据e^iqna的正交性和拉普拉斯函数，最终可得哈密顿量H为

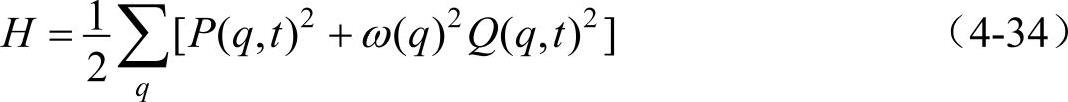(www.xing528.com)

式中，，。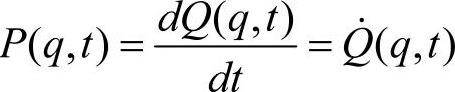

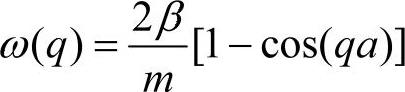经过变换后，哈密顿量（总能量）已不包含交叉项，成为经典谐振子哈密顿量之和，新的动量和空间坐标已不是原来原子的动量和空间坐标，而是反映整体运动的坐标，它称为简正坐标。

根据经典哈密顿量式（4-34），可以直接用来作为量子力学分析的出发点，此时要把P（q，t）和Q（q，t）看做量子力学的正则算符，那么哈密顿量变为

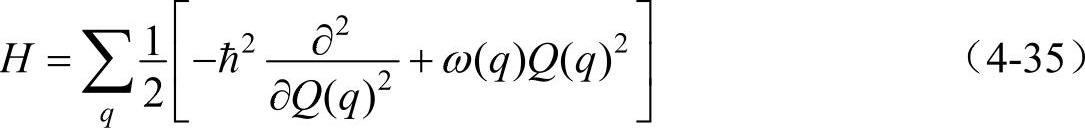
相应的薛定谔方程为

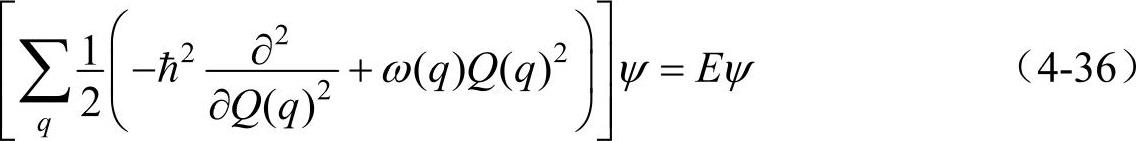
式（4-36）中的E即（4-35）的H。式（4-36）是量子力学中的一系列独立简谐振子的薛定谔方程。其独立简谐振子的能量ε为

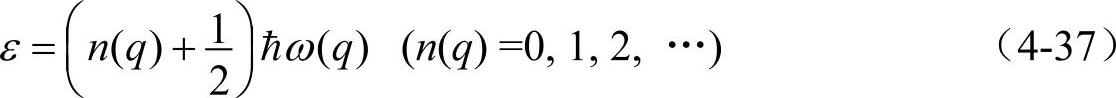
ε是量子化的。一维晶格振动的总能量E为

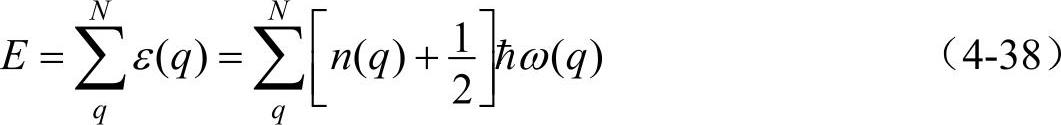
式中N为一维晶格的原胞数，它等于独立简谐振子数。由玻恩—冯卡门边界条件也可看出，q只能取N个不同的值。