声光波的传播原理与特性

再来讨论复式格子中两支格波的色散关系。ω₁^一支的色散关系式（4-15）可改写为

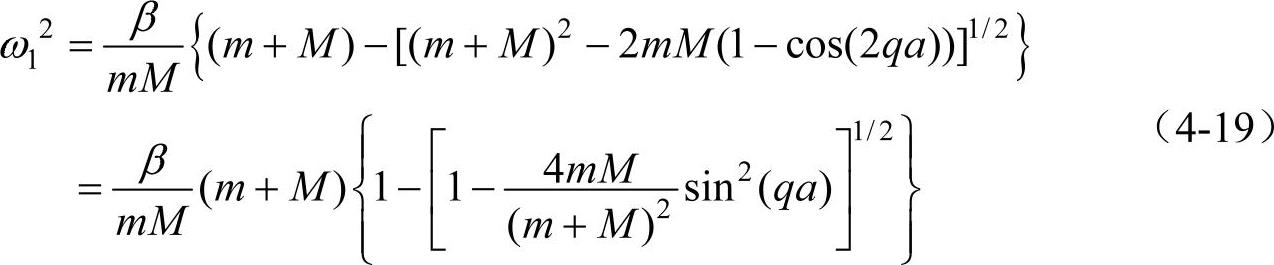
如果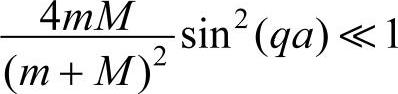（这在实际上是成立的），则式（4-19）近似地化为

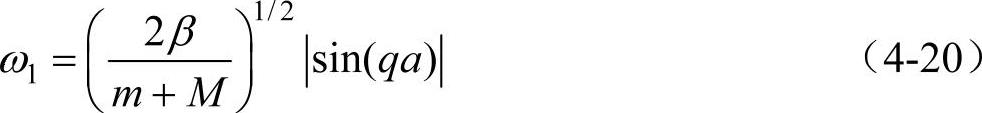
把式（4-20）与式（4-6）比较，可见ω₁^一支的色散关系与一维布喇菲格子的情形形式上是相同的，也具有如图4-2所示的特征。这也就是说，由完全相同原子所组成的布喇菲格子只有声学波。

ω₂一支的色散关系式（4-16）则可改写为

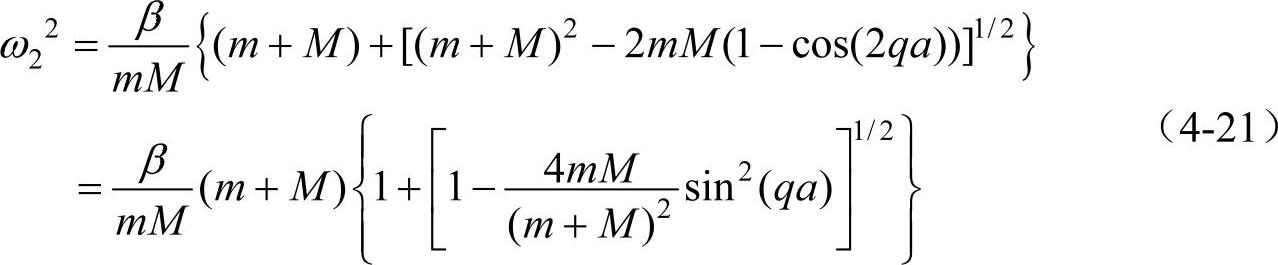
在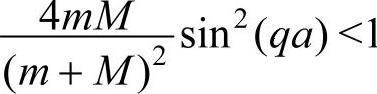的条件下，则式（4-21）近似地化为

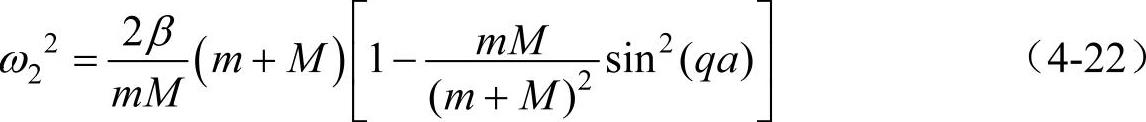
可见，当q→0（即波长λ很大）时，光学波的频率具有最大值为

其中_μ=mM/（m+M）是两种原子的折合质量。而当q→0时，由式（4-20）看出，ω₁→0，这时，声学波频率则为最小。

综合本节以及式（4-17）和式（4-18）的结果，归纳如下：①声学波的频率ω₁最大值为（2β/M）1/2（当q=±π/（2a）时），最小值为0（当q→0时）。②光学波的频率ω₂最大值为（2β/μ）1/2（当q→0时），最小值为（2β/m）1/2（当q=±π/（2a）时）。

一维双原子复式格子中，声学波与光学波的色散曲线如图4-5所示。(www.xing528.com)

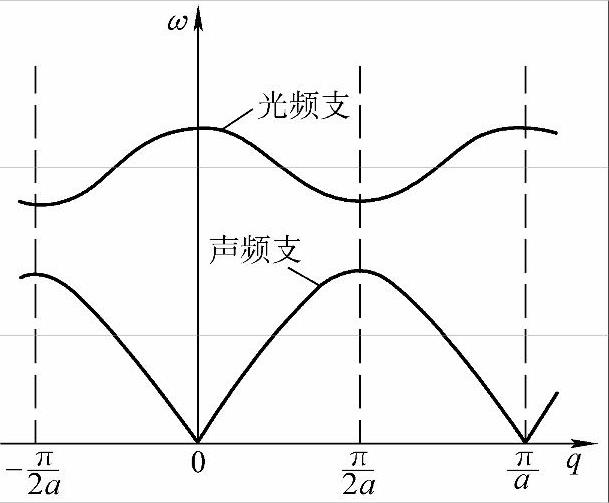
图4-5 一维双原子复式格子的振动频谱

再看相邻两种原子振幅之比，这由式（4-12）决定。对于声学波，相邻两种原子振幅之比为

因为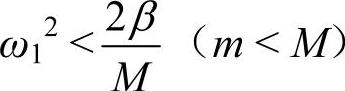，而一般cos（qa）>0，所以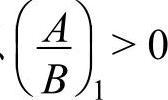。这就说，相邻两种不同原子的振幅都有相同的正号或负号，即对于声学波，相邻原子都是沿着同一方向振动的，其振动概况如图4-6所示。当波长相当长时，声学波实际上代表原胞（由异质两原子组成）质心的振动。

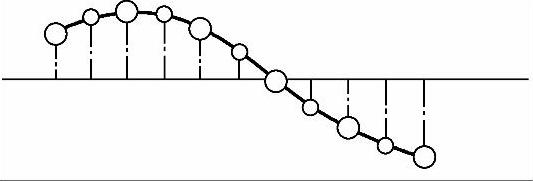
图4-6 声学波示意图

对于光学波，相邻两种原子振幅之比为

因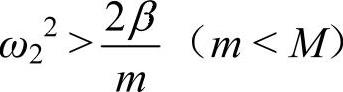，而一般cos（qa）>0，所以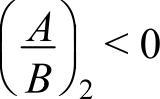。由此可见，对于光学波，相邻两种不同原子的振动方向是相反的。而当q很小时，cos（qa）=1，又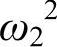=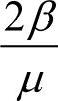，得出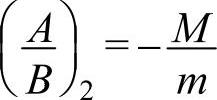。因此对于波长很长的光学波（长光学波），mA+MB=0，即原胞的质心保持不动。由此也可定性地看出，光学波是代表原胞中两个原子的相对振动。光学波的振动概况如图4-7所示。

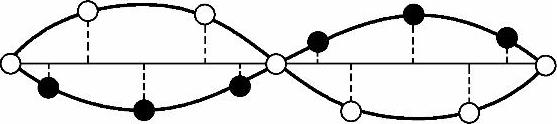
图4-7 光学波示意图