一维复式格子振动优化方案

为简单起见，考虑由两种不同种原子所构成的一维复式格子，相邻同种原子间的距离为2a（2a是这复式格子的晶格常数），如图4-4所示。质量为m的原子位于2n-1，2n+1，2n+3，…各点；质量为M的原子位于2n-2，2n，2n+2，…各点。原子振动是一维的。类似于式（4-3）得到

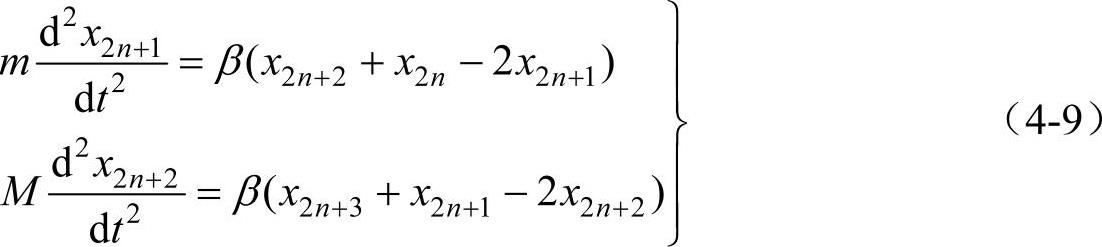
为明确起见，这里假设M>m，与式（4-3）相似，方程组（4-9）的解也可以是角频率为ω的简谐振动

由于这里包含有两种不同的原子，这两种不同原子振动的振幅，一般来说也是不同的。

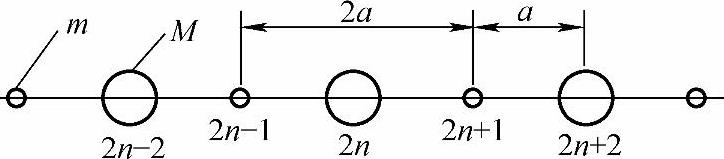
图4-4 一维复式格子

把式（4-10）代入式（4-9），得

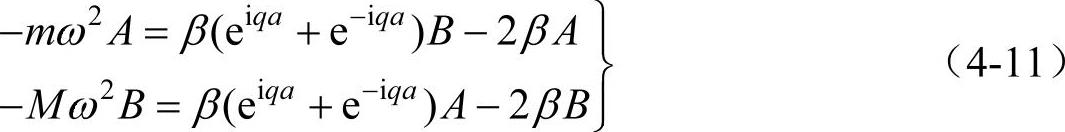
上式又可改写为

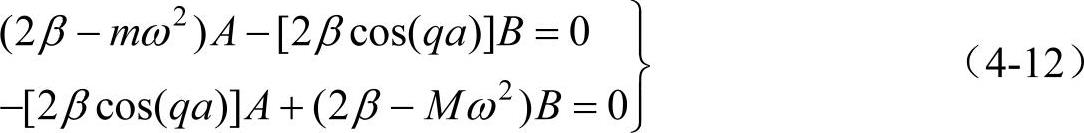
若A、B有异于零的解，则其系数行列式必须等于零，即(www.xing528.com)

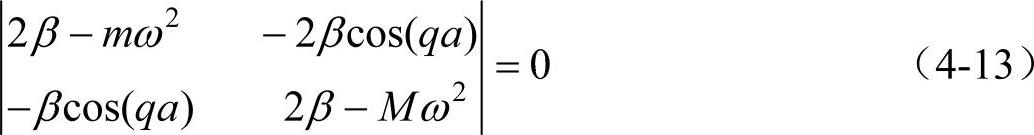
由此可以解得

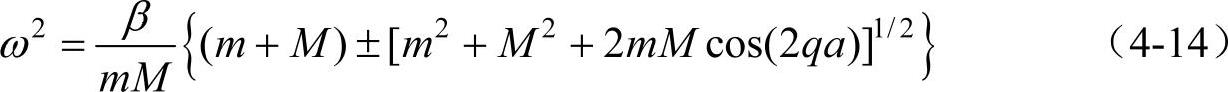
由上式可以看到，ω与q之间存在着两种不同的色散关系，即对一维简单复式格子，可以存在两种独立的格波（这一点是与前面所讨论的一维简单晶格不同，对于一维简单晶格，只能存在一种格波），这两种不同的格波各有自己的色散关系

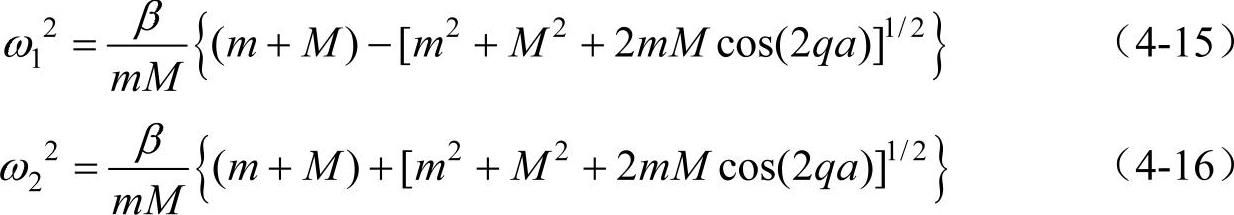
为了便于进一步讨论这两支不同格波的性质，就需要知道qa取值的范围。在考虑一维的简单晶格格波的色散关系时，已取qa属于区间（-π，π）。同样，对于一维复式格子，为了保证波函数的单值性，则把q值限制在（-π/（2a），π/（2a）），其中2a是这复式格子的晶格常数。

现在再看式（4-15）和式（4-16），因为2qa限制在（-π，π），所以ω₁的最大值为

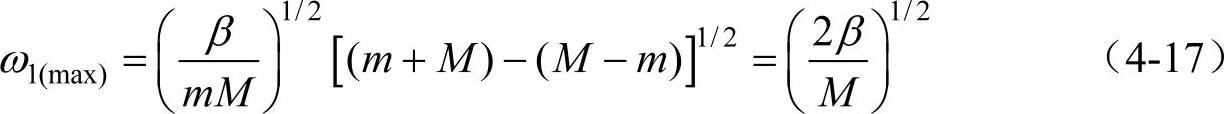
而ω₂的最小值为

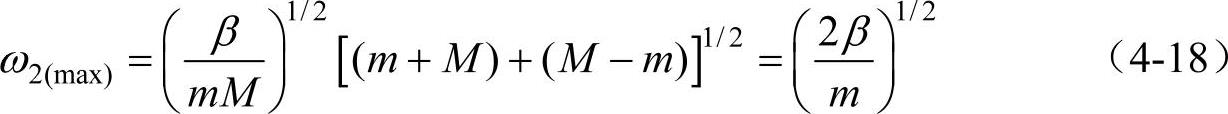
因为M>m，从而ω₂的最小值比ω₁的最大值还要大。换句话说，ω₁^一支的格波频率总比ω₂^一支的格波频率为低。实际上，ω₂^一支的格波可以用光来激发，所以常称为光频支格波，简称为光学波。而ω₁^一支格波则称为声频支格波，简称为声学波，命名起因于这样一个事实，当q很小时，该格波表现为长波长的弹性波，其频率与速度无关，频率与波矢是线性关系，与弹性波相似，而纵弹性波与声波是等同的。现在，由于高频超声波技术的发展，ω₁^一支也可以用超声波来激发了。