一维晶格振动的简单模型分析

如图4-1所示的一维原子链，每个原子都具有相同的质量m，平衡时原子间距（晶格常数）为a。由于热运动各原子离开了它的平衡位置，用x_n代表第n个原子离开平衡位置的位移，第n个原子和第n+1个原子的相对位移为x_n+1-x_n。不但原子链是一维的，原子的振动也是一维的。下面先求由于原子间的相互作用，原子所受到的恢复力与相对位移的关系。

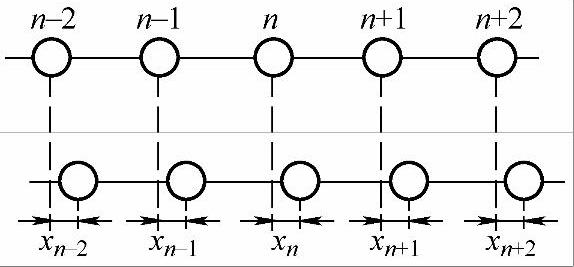
图4-1 一维单原子链的振动

设两原子的互作用势能是U（r），r为两原子间的间距。在平衡位置时，两个原子间的互作用势能是U（a），令δ=x_n+1-x_n，则产生相对位移后，相互作用势能变成U（a+δ）。将U（a+δ）在平衡位置附近用泰勒级数展开，得到

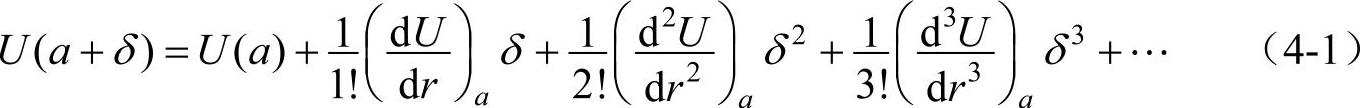
式中首项U（a）为常数，次项为零（因为平衡时势能取极小值）。又因δ很小，势能展开式（4-1）中可只保留到δ²（后面的项为非简谐项）。这时两原子间的恢复力F为

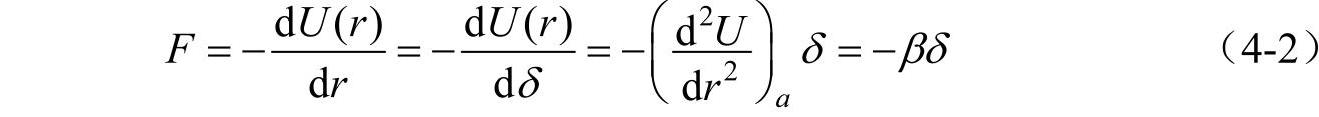
式中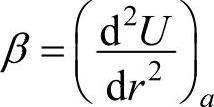。式（4-2）指出，当相对位移很小时，β为常数（称为恢复力常数），作用力为准弹性力，与δ成正比，此方法叫简谐近似。

第n个原子除受第n-1、n+1相邻原子作用外，还受其他原子的作用，即受整个晶体原子的作用，为了简化只考虑相邻原子的互相作用。第n个原子的运动方程为

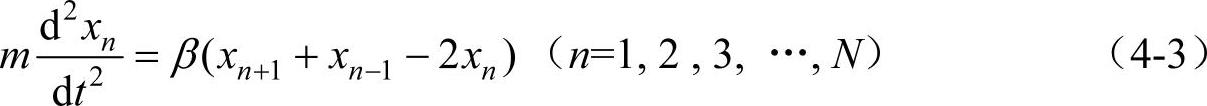
N为晶体的原子数。对于每一个原子，都有一个类似的运动方程，因此方程数目和原子数目相同。

设式（4-3）的解是一振幅为A，角频率为ω的简谐振动

式中，qna表示第n个原子振动的位相因子，即第n个原子与第0个原子振动的位相差，显然相邻原子的位相差是qa；q=2π/λ，令n代表沿格波传播方向的单位矢量，则q=（2π/λ）n称为波矢；λ为波长。将式（4-4）代入式（4-3），可得

(www.xing528.com)

亦即

式（4-6）称为一维单原子晶格振动的色散关系式。不同的q对应着不同的ω，即不同的波矢的波，波速（相速）υ_p=ω/q不同。

如果第m个和第n个原子的位相因子之差（qma-qna）为2π的整数倍，即ma-na=2πs/q（s为任意整数）时，

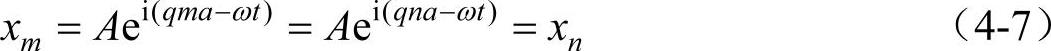
由式（4-7）可得出如下结论：①第m个和第n个原子的距离（ma-na）为2π/q的整数倍时，原子因振动而产生的位移相等。这样可以看成m原子振动引起了邻近原子的振动，依次传播下去，引起n原子振动与m原子振动完全相同。这就说明原子在平衡位置附近的振动以前进波的形式在晶格中传播，这种由于晶格振动发出的波叫做格波。在晶体中格波是所有原子以相同频率，彼此之间有一定位相差的集体运动。实际上这种集体运动形成一个准连续的波。②当s=1时，即ma-na=2π/q。由于两振动相同的原子间距离为波长，所以格波的波长λ=2π/q。③波数范围的限制——格波限制条件。由色散关系式（4-6），若q′=q+2πg/a时（g为任意整数），则

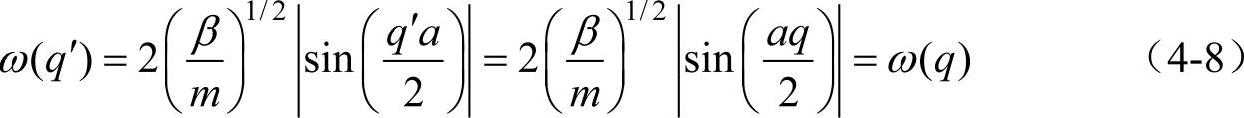
由式（4-8）可知，当q′与q相差2πg/a时，代表格点相同的振动状态，为了使振动状态与q的单值性对应，所以把q限制在主值区域（-π/a，π/a），该区域称为格波的限制条件。

由色散关系式（4-6）可知，当q很小时，即在长波的情形下，sin（qa/2）≈qa/2，所以ω=（β/m）1/2aq。即长波时频率与波矢是线性关系，与弹性波相似。这时波速_νp=a（β/m）1/2=（E/ρ）1/2，E是弹性模量，ρ为线密度，νp是常数。当q很大时，即在短波的情形下，由sin（aq/2）最大值为±1，ω有最大值，ω_max=2（β/m）1/2，一维简单晶格的q与ω关系如图4-2所示。ω随q呈周期性变化。+q对应前进波，-q对应与前进波方向相反的波。

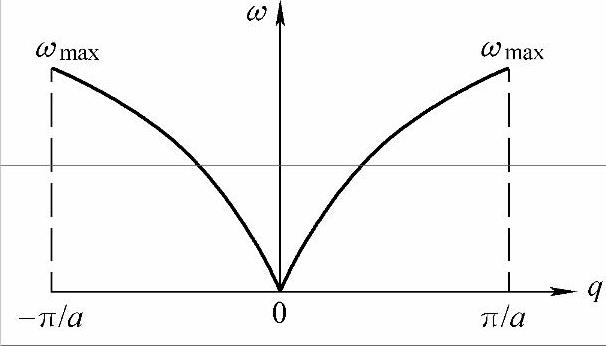
图4-2 一维简单晶格（即布喇菲格子）的q与ω关系

原子在平衡位置的振动以波的形式在晶体中传播，一维简单晶格振动的波形如图4-3所示。

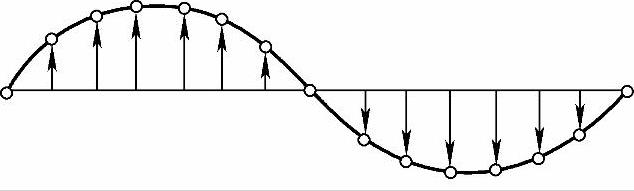
图4-3 晶体中原子在平衡位置的振动