合金中的能带优化研究

金属元素可以互相溶解形成固容体或者进行化合形成化合物，另外也能形成电子化合物中间相。中间相这种化合物是由两种金属组成的，其一种为一价的金属（如Cu、Ag、Na等）或过渡金属（Mn、Fe、Co等），而另一种为二至五价的金属（如Be、Mg、Zn等）。这种化合物的特点是，价电子数与原子数之间具有一定的比例，即3：2、21：13、7：4等，每一比值均对应于一定的晶格结构。例如成分CuZn、Cu₃Al及Ag₃Al的合金相，虽然它们的原子百分数很不相同，但价电子总数与原子总数之比（称电子浓度）相同，即为1.5。它们的晶体结构都是体心立方结构。Hume Bothery研究电子化合物得出：当电子浓度为3：2时，化合物具有体心立方结构（β相）。当电子浓度为21：13时，具有复杂的立方晶体结构，单位晶胞有52个原子（γ相）。电子浓度为7：4时，具有密排六方晶格结构（ε相）。电子浓度决定电子化合物的规律可用金属电子论解释。

图3-38为面心立方晶格和体心立方晶格晶体的状态密度曲线。当电子所占的最高能级尚未达到面心立方晶体的第一布里渊区边界或者在布里渊区边界左右时，排布同样的电子数，面心立方晶格晶体的总能量ε_fcc小于体心立方晶格的总能量ε_bcc，面心立方晶体稳定。但是随着电子数N的增加（超过布里渊区边界），面心立方晶体的电子密度a（ε）急剧下降，而体心立方晶体的电子密度a（ε）急剧上升。以致ε_fcc大于体心立方晶格的总能量ε_bcc，这时晶体结构以体心立方稳定。据此可以求出面心立方晶格，体心立方晶格以及其他晶格稳定时的最大电子数。

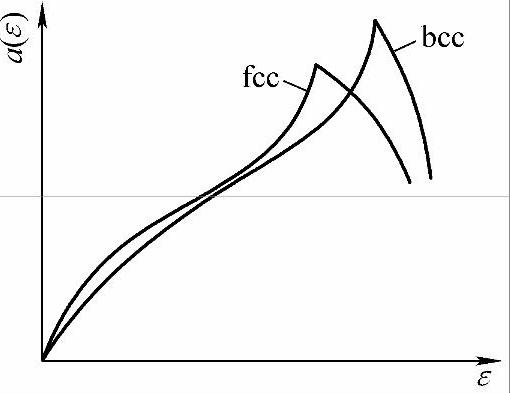
图3-38 fcc、bcc晶体状态密度曲线示意图

面心立方晶格的第一布里渊区为多面体（14面体，8个六角形面和6个正方形面组成），估计晶格稳定的最大电子数时，以等能面为球面近似，球面的半径是最短的满足布里渊区边界条件的波矢k。对面心立方晶格，晶格常数为a，则k等于布里渊区中心到六角形面的距离，亦等于体心立方格子中心到任意一个角的距离之半（也就是体心立方对角线的1/4）。面心立方倒格子为体心立方格子，格子边长为2/a（体心立方倒格子为面心立方格子，格子边长为a）。则

设晶体中有N个原子，在面心晶格中单位原胞包含4个原子，每个原子所占的体积为a³/4。故晶体的体积V=Na³/4，亦等于k空间的状态密度（不计自旋），即V=dN/（dk_xdk_ydk_z），这里dk_x、dk_y、dk_z为k空间的三个分量。由于在k空间的状态密度为2V（计入自旋）。则在球内能容纳的最大电子数N_e等于球体积乘以2V，即

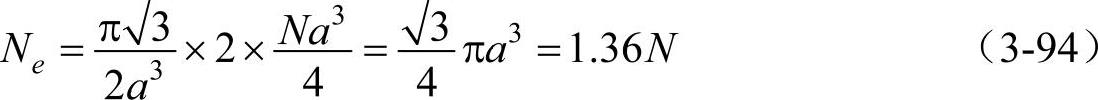(www.xing528.com)

因此，在面心立方相，当每个原子平均有1.36个价电子时，电子正好填充到距原点最近的布里渊区边界上的能级。

同理，可以算出体心立方晶格对应等能面为球面近似的布里渊区能含的最大电子数N_e为

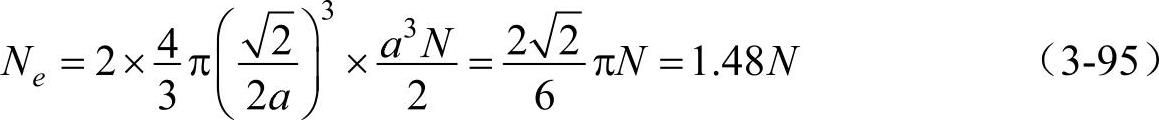
就是说，当每个原子平均有1.48个价电子时，电子正好填充到同12面体的面相接触的能级。

上述讨论得出金属电子论可以说明电子化合物的形成，主要决定于电子浓度的规律。仔细讨论起来，问题并不那么简单。①在一些包含过渡元素的中间相中，过渡元素的价数如何确定，如CoAl、NiAl、FeAl等合金相是体心立方结构，欲归类于3：2的电子化合物，则Co、Ni、Fe等过渡元素为零价。但从另外一些合金相，如CrAl₇、Co₂Al₉、MnAl₆、FeAl3等发现，当过渡元素的d带中空穴数减少时，铝的含量也相应减少，因而设想铝的价电子填入到d带，过渡元素似乎具有负的价数。②布里渊区多面体，以最小k的球面近似计算最大电子数是建立在假定球形的等能面碰到布里渊区边界时才发生畸变。但有人测Cu的等能面，发现尚未碰到布里渊区边界时球形的等能面早巳发生畸变。③分析表明，组元有明确的价的情况下（例如Cu为1价，Zn为2价，Ga为3价）溶质原子的s+p电子不一定全部进入导带，而有可能束缚在溶质原字上。Mott指出：Zn、Ga、Ge溶于Cu中至少贡献一个电子给导带，第二个电子或在导带或在束缚带，Ga、Ge的第三个电子肯定在束缚带，这一点可以用组元在纯态的第二电离能佐证。Zn的第二电离能是解离成二价离子所需的能量，为ε₂，金属晶体的结合能为ε_b，则

式中，ε₁为溶剂的一次离化能；V（r₀）是溶剂原子实与价电子的吸引势能；是零点平均动能。如果ε₂<V（r₀），则第二个电子可能进入导带，研究得出Cu的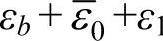=15.35eV。而Zn、Ga、Ge的第二电离能分别为17.89eV、20.4eV、15.36eV，既然溶质原子的价电子不一定全部进入导带，合金的价电子如何计算就成为问题。