有效质量与波矢大小的关系

本小节讨论晶体电子对外力F的响应。当外力等于零时，晶体电子还受到晶格势场的作用，它对电子运动的影响已概括到能量函数ε（k）中，其值可通过解薛定谔波动方程求得。在有外力F作用时，电子除了和外力作用外，还和晶格相互作用着。电子的加速度实际上是外力F和晶格内部相互作用力F_l综合作用的结果，即a=dν/dt=（F+F_l）/m*。讨论电子对外力的响应时，可引入已概括了电子与晶格相互作用的有效质量m*来描述，把电子在外力作用下的加速度同外力F的关系写成类似牛顿第二定律的形式，即

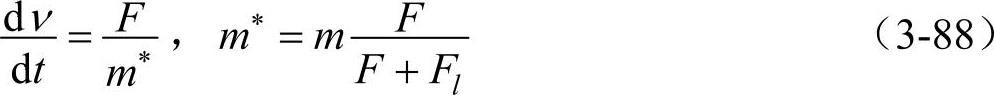
因此，晶体电子对外力的响应就像具有质量为m*的自由电子。

m*的数值可从ε（k）求得。由于等能面的各向异性，沿k空间不同的方向，电子的有效质量是不同的。类比自由电子的情况，在一维情况下，认为m*与ε（k）的关系仍是式（3-85），只不过将m换成m*而已，然后方程再对k求导，得

m*随波矢k变化的定性曲线如图3-32c所示。(www.xing528.com)

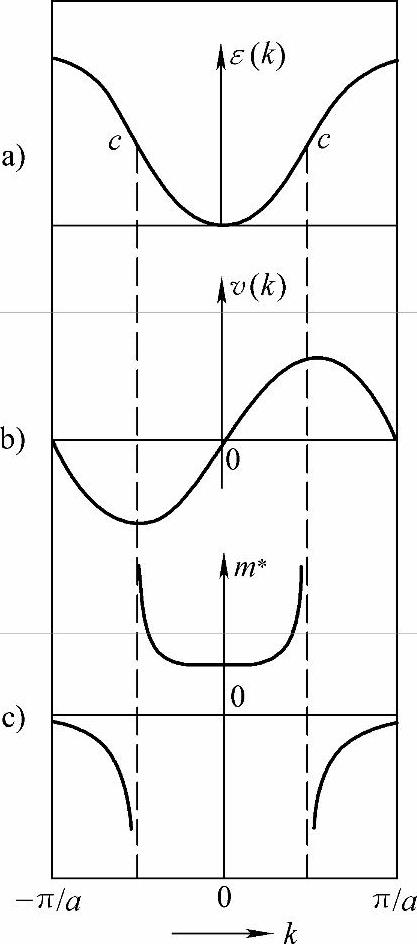
图3-32 一维能带中的电子速度和有效质量

a）能带 b）速度 c）有效质量

不同的能带，电子的有效质量不同。在同一能里，有效质量m*反比于ε（k）曲线斜率的变化率。图3-32中，在能带的下半部，由于电子的运速度随波矢的线性增加，使有效质量保持为一正常数，相当于电子在外力作用下作加速运动。在c点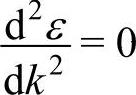，，m*→∞，相当于外力F对晶体电子不产生任何效应。在能带的上半部（c点以后），由于随k增加而减小，加速度变为负值，在外力方向保持不变的情况下，这个结果等效于有效质量的符号从正变为负。加速度为负值也说明了当晶格传递给电子的动量大于外力传递给电子的动量时，电子能够克服外力的影响而作负的加速运动。

有效质量的表达式直接反映了能带的曲率，也就是说能带的宽窄与有效质量有直接的关系。所以用有效质量的概念不但能够形象地像讨论自由电子一样来讨论晶体中电子的运动，而且由于有效质量与能带结构有关，因而有助于对能带结构的研究。