电子速度与波矢k的关系

在第2章中已阐明沿某一方向运动的波包的群速度u_g=dω/dk（ω角频率，k为波数），电子运动的速度等于布洛赫波组成波包的群速度，即电子运动速度ν（k）=u

g=dω/dk。对于物质波，粒子的能量E（k）=hν=ћω，那么对自由电子运动的运动（总能量中只有动能），ν（k）为

这里m为电子的质量。用矢量表示速度的方向和波矢的方向，则

∇是矢量微分算符。ν（k）沿球形等能面法线方向（k方向），并与波矢k成正比，如图3-31a所示。

处于晶体中的电子（布洛赫电子），其运动速度等于波包中心的群速度，它与k空间的能量梯度成正比，即

(www.xing528.com)

速度ν（k）的方向沿等能面的法向。由于晶格周期场势的作用，其等能面并非总是球形等能面，ν（k）与k并不总是同向，大小也不一定等于ħk/m（但等于ħk/m*，m*为电子有效质量，后面叙述）。其ν（k）～k关系如图3-31b所示。

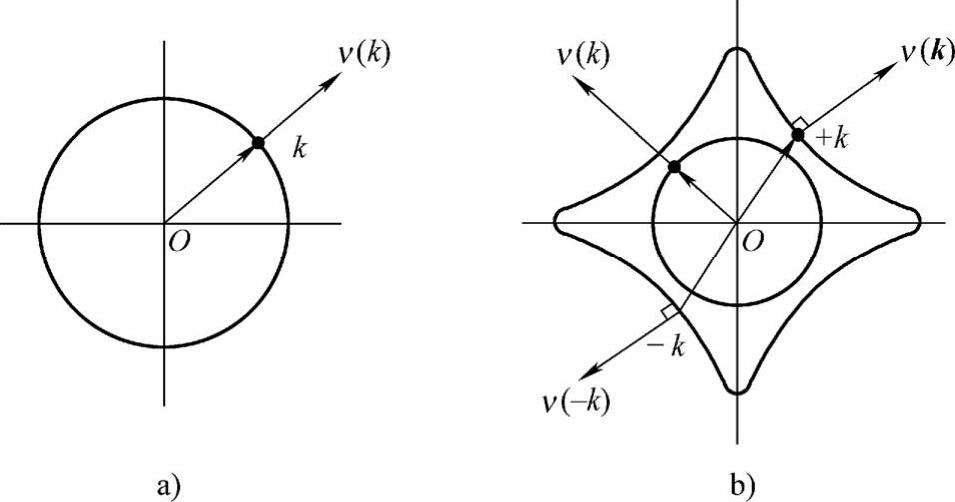
图3-31 电子的速度矢量

a）自由电子 b）布洛赫电子

电子的能量ε（k）具有周期性，同时也具有与晶格相同的对称性，因而ε（k）=ε（-k）。从式（3-78）可知，k和-k态，ε（k）函数具有数值相等符号相反的斜率，因此ν（k）=-ν（-k），如图3-31b所示。这个关系式是讨论导体、绝缘体和半导体能带的一个重要公式。

最终根据能量梯度求得的一维情况下的电子速度如图3-32所示。在能带低，k很小，晶格散射对电子运动的影响很小，ν=ħk/m，与自由电子类似（图3-32b）。随着k的增加，晶格散射增强，当k增大到布里渊区边界时，电子遭受到强布喇格反射，散射波增强到与入射波相同（但传播方向相反），这时电子速度为零。在ε（k）～k曲线的拐点处（图3-32a中的c点）电子能量最大。