准自由电子近似方法解析及应用

1.一维晶体准自由电子近似

假定晶格周期势场对电子的作用很弱，电子几乎是自由地运动着，这时可以认为电子的行为和量子自由电子论中讨论的自由电子相同。但是，又有一点特殊，当电子波的波长λ（或波数k）满足布喇格衍射条件时电子将受到由晶格势场引起的布喇格反射而形成驻波，不能在晶体中传播。例如，晶格常数为a的一维晶体（图3-14），当波数为k=πn/a（n为整数）的电子波exp（ikx）入射时，由相邻原子引起的两个反射波的光程差为2a，相位差为k2a=2nπ，两个反射波同相位，满足布喇格反射条件式而互相增强。所以，这个波数的电子受到全反射而不能在晶体中行进，具有与此波数相应能量的电子在晶体中不存在。

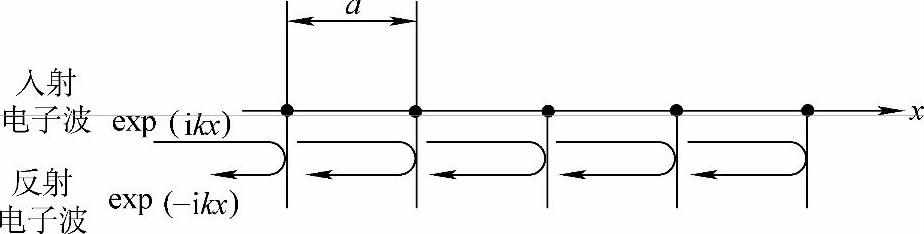
图3-14 一维晶格中电子波exp（ikx）的布喇格反射

下面更详细地讨论一下这一点。一维晶体（晶格常数为a，长有N个晶格常数）中，电子的波动方程为

脚标k表示波函数ψ（x）是由分立的波数k确定的（波函数ψk（x）布格赫函数，波数k=2πg/（Na），g是0≤g≤N-1区间中的整数。）。V（x）为晶格的周期势场，在准自由电子近似中认为ε_k》V（x）。因为V（x）具有和晶格相同的周期a，所以可以展开为如下的傅里叶级数

式中展开系数V_n=γv_n为

若把能量原点选在V（x）的平均值（1/a）为零处，则当n=0时V₀=0。另外，系数γ为远小于1的常数，对于自由电子γ=0。

满足式（3-61）的波函数是式（3-45）的布格赫函数，所以具有和晶格势场相同周期的函数u_k（x）也能展开为如下的傅里叶级数

因此

对于自由电子，V（x）=0（在式（3-62）中γ=0）波函数ψk（x）=b₀exp（ikx），因此式（3-65）的布格赫函数近似地可写成

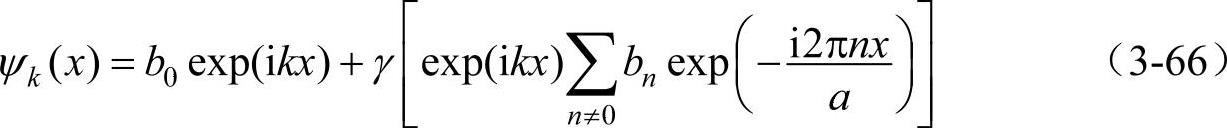
式（3-66）满足布格赫条件式（3-46）。

把式（3-62）、式（3-66）代入式（3-61），最终求得二级近似的能量本征值ε_k为

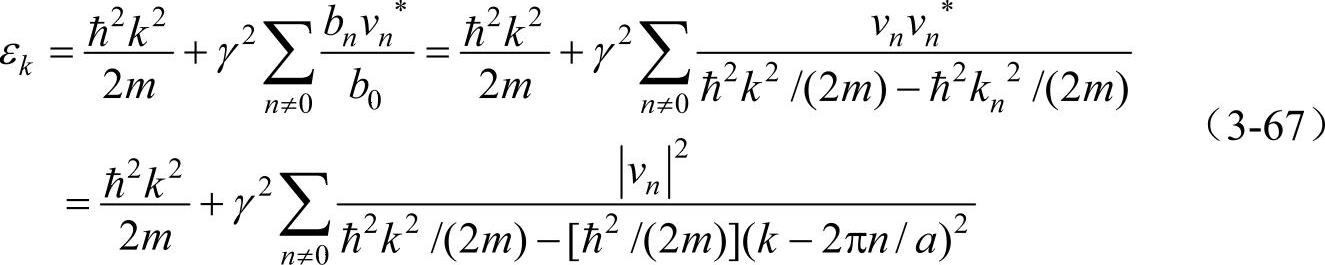
式中v_n*为v_n的共轭复数，k_n=k-2nπ/a。当k²不趋近任一个k_n²时，式（3-67）能够给出准确的近似解。但是，当k²≈k_n²时，尽管γ非常小，式（3-67）的右边第二项仍是发散的。这时不能把式（3-66）作为波函数的近似。当k²≈k_n²时，也即k=k-2πn/a或者k=nπ/a时，可最终求得能量本征值ε_k为

即满足布喇格衍射条件能量发生2V_n的跃变，出现了禁带。由上面的自由电子近似，可以得到如图3-15所示的电子能量ε_k与波数k的关系。

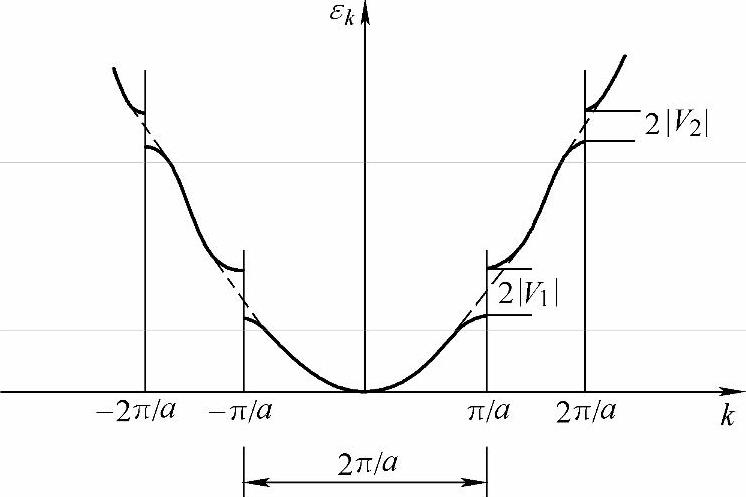
图3-15 自由电子近似的一维晶格电子能量ε_k和波数k的关系

2.晶体中准自由电子近似

（1）k空间与布里渊（Brillouin）区

上面讨论了一维晶体的ε-k关系及允许带和禁带，现在讨论三维晶体。在三维晶体中，可以建立一个波矢k空间来表示电子的能量状态。k大小等于2π/λ（波数），方向表示电子波受布喇格衍射前的运动方向。波失k空间由相互垂直的三个波矢分量k_x、k_y、kz的坐标轴组成，与在实际空间中平行于x、y、z轴的波运动相对应。一般选择x、y、z轴使之与晶体的相应轴平行，例如在立方系中k_x、k_y、k_z与单位晶胞相应的三条相互垂直的棱的方向平行。在k空间中，等能面上各点的垂直方向即为电子运动的方向。周期场中运动的电子，由于周期排列的金属离子的作用，这时在k空间中的等能面有的不是球面。电子运动的方向仍与等能面垂直，但往往与过原点连线方向不一致。

应用k空间的概念可以描述在二维及三维晶体中波矢与电子能量的关系。为了方便起见先从二维点阵入手，以后再推广到三维中去。设电子在二维正方点阵中运动，如图3-16a代表离子的一个简单正方点阵。图3-16b代表相应二维波矢空间，k_x和ky平行于正方形的两边。在图中画出一条任意直线0A，它代表在相同波运动方向上的一系列电子状态。当k值增加时，在ε_k-k曲线上响应点出现能量间隙。现假设在图3-16c中，线p₁、p₂、p₃代表晶体中的离子排列，FG方向同图3-16b中0A方向。一般情况下，由0A上的波矢来表示其状态的电子将通过这些离子列而很少散射。少数电子的波长能满足布喇格方程而发生强烈反射，电子不能通过点阵。如果要过渡到更高的波矢，能量将有一个陡增，在波矢图3-16b中，将有a₁、a2、a3^等一系列波数的点能满足布拉格方程。从0到a₁、a₁到a₂、a₂到a₃等波失区间中能量是连续增加的，但在a₁、a₂、a₃等处，能量是急剧增加的。

可以具体计算符合反射条件的k值。当波长为λ的电子波在晶体中沿某一方向运动时，当某一晶面的间距d和该晶面与电子波运动方向的夹角θ满足布喇格方程nλ=2dsinθ时，发生全反射。这时，当n=1时，k=2π/λ=π/（dsinθ）。对于图3_-16a所示二维晶格中的BE、CD面来说，d=a，电子沿ED方向运动，θ=90°，则k_x=π/a，即当k_x=π/a时符合衍射条件；对BC、ED面来说，d=a，电子沿EB方向运动，θ=90°，当k_y=π/a时符合衍射条件；对于BE、CD面，如果电子运动方向与该组晶面成45°，即θ=45°，则k₄₅°=2¹/2π/a。同理可求得各个不同方向符合反射条件的k值，如图3-16d中的a₁₁、a₁₂、a₁₃所示。连接这些点形成的多边形（包括多边形的内部）称为二维结构的第一布里渊（Brillouin）区。同样，图3-16b中的a₂是第二个多边形边界上的一点，第二个多边形为第二布里渊区边界。布里渊区的意义是：它的边界上k值的能量是不连续变化的，而布里渊区内部能量随k值连续变化。每个晶体结构有自己特定的布里渊区，它由晶体结构的几何性质来决定的。一个简单正方点阵的第一、第二、第三布里渊区如图3-17所示。

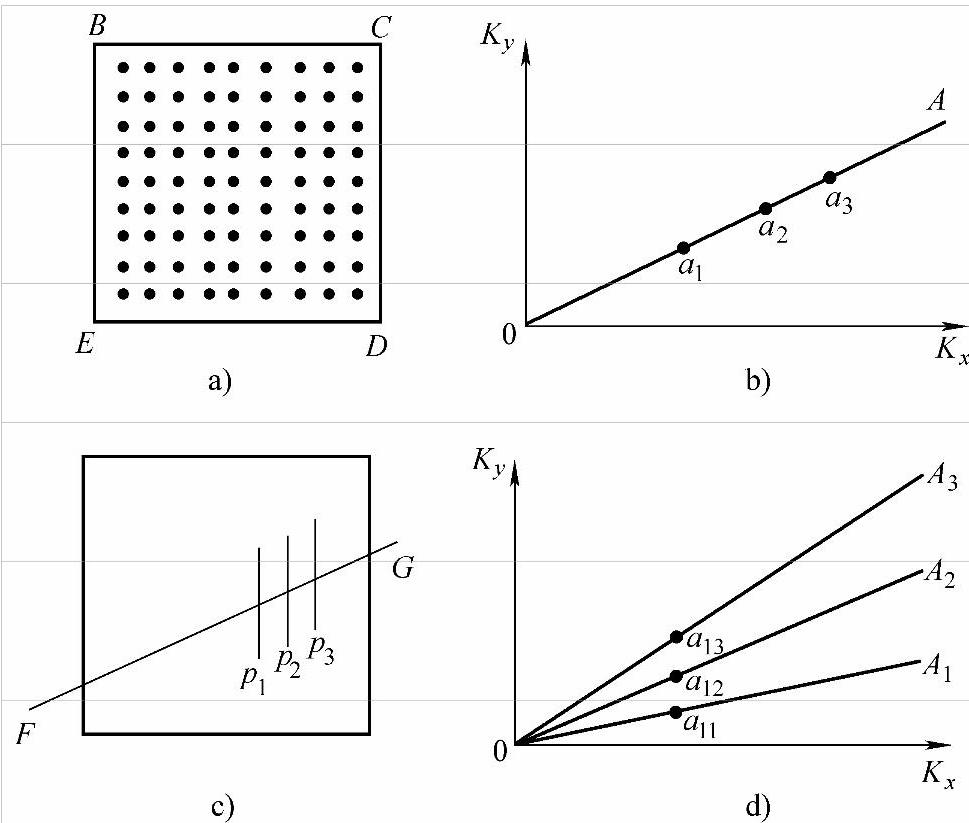
图3-16 受到反射的k值(www.xing528.com)

同样的原理也适用于三维晶体，只要把二维波矢代之以三维波矢。在三维波矢空间中，找出任意方向上的能态符合布拉格反射的波数临界值点。连接这些点，形成三维的布里渊区。简单立方点阵晶体，其第一布里渊区是一个以2π/a为边的立方体，重心与原点重合。面心立方点阵与体心立方点阵的第一布里渊区分别如图3-18和图3-19所示。

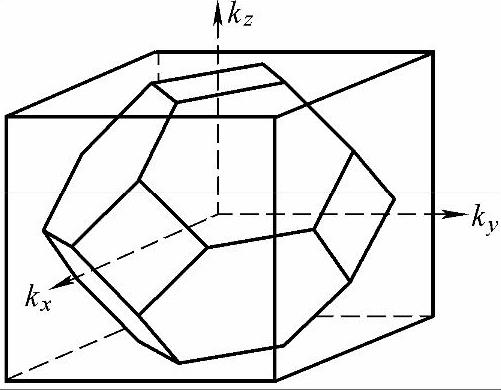
图3-18面心立方点阵的第一布里渊区（图中的多面体）

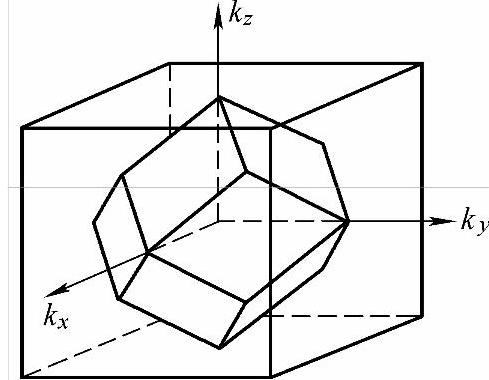
图3-19 体心立方点阵的第一布里渊区（图中的多面体）

应该说明的是，布里渊区不是真实的空间晶体，它是k空间的图像。

（2）布里渊区与能带

在波矢k空间中，电子能量相等的点（k_x，k_y，k_z）连成的面称为等能面。可根据电子的ε-k关系画出等能面。现在考查一下电子在k空间中的布里渊区里的分布。设想在离子构成的金属晶体中逐点加入“准自由电子”，电子将自低能态向高能态逐步填充。在二维正方点阵的情况下，准自由电子近似的等能线如图3-21所示。K值较小能量低的等能线1、2距布里渊区边界较远，是以原点为圆心的圆。这是因为波数与临界值（满足布喇格衍射条件的值）相差较大的电子与自由电子近似。这些电子没有周期场给予它们的方向性，所以不论运动方向如何，都有同样的ε-k关系。当k值继续增大（等能线3），等能线开始偏离圆形，它在接近布里渊区边界处向外突出。这是因为在边界处周期场的影响显著。另外从ε-k曲线上也可看出，在接近临界k值处，ε-k曲线偏离到自由电子的抛物线以下，ε随k值缓慢地增加。因此在k空间的这个区域里，能量从一个等能线增加到另一个等能线，k值有一个较大的增值。再高的等能线如等能线4、5，已与布里渊区边界相交，表明具有这个范围的能量的电子状态位于布里渊区的角部，处于布里渊区角顶的能级在这个布里渊区中能量最高。因为在布里渊区的边界上能量是不连续的，等能面不能穿过布里渊区边界。若把第二个布里渊区等能量的几条线也画出，就是如图3-20所示的第一布里渊区以外的那几条。布里渊区边界虽有能量垒存在，但整个晶体不一定有禁带。若第一区k_y方向最高能级P为3.0eV，这个方向的垒高为2.0eV，则第二区最低能级R为5.0eV。若第一布里渊区的最高能级Q为4.5eV，这种情况下，第一布里渊区的最高能量低于第二布里渊区的最低能量，则整个晶体就有禁带存在，第一、第二布里渊区能带是分立的。若第一布里渊区的最高能级Q为5.5eV，在这种情况下，整个晶体便没有禁带，第一和第二区能带重叠。两种情况电子在布里渊区的填充如图3-21所示。图中1、2、3、4表示布里渊区的各个充填阶段，已充填的区域画有影线。图3-21a为具有禁带的情况；图3-21b为无禁带的情况。

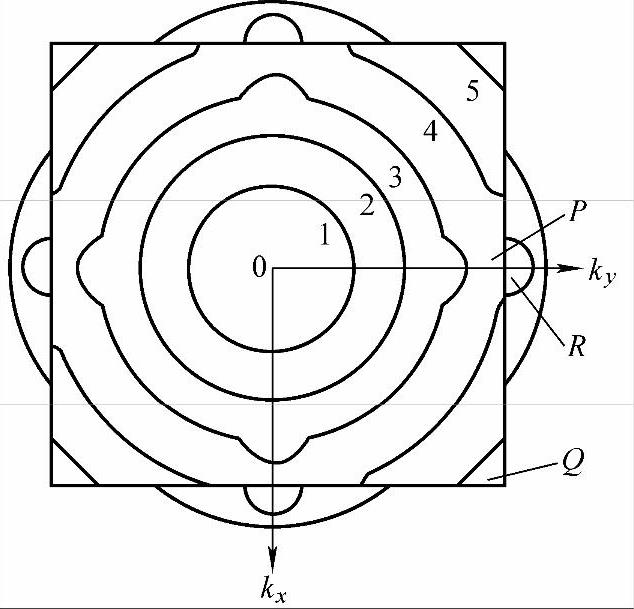
图3-20 二维正方点阵第一、二布里渊等能线

图3-21 电子填充布里渊区的不同阶段

a）无重叠布里渊区 b）有重叠布里渊区

上述情况如用ε-k曲线表示，则如图3-22所示。图3-22是把几个不同方向的电子波ε-k曲线叠放在一个平面图上而得出的。在图3-22a中，可看到第一布里渊区中最高点c低于第二布里渊区能量最低点a′，这说明不存在能带重叠。图3-22b示出的是能带重叠的情况，即虽在任意一个方向上无能带重叠，但各个方向组合在一起，第一布里渊区的能量最高点c高于第二布里渊区的能量最低点a′，故该晶体属于能带重叠型的。是否存在能带重叠对晶体性能影响极大。

图3-22 不同方向的ε-k曲线叠放在一个平面图上的表现

a）无能带重叠（有禁带） b）有能带重叠（无禁带）

（3）电子状态密度分布

当电子充填k空间的最初阶段，状态密度ρ（ε）与能量ε的关系曲线如量子自由电子模型那样呈抛物线。当在k空间中表示被占状态的球扩大且接近布里渊区边界的最近点时，ρ（ε）-ε曲线就开始偏离抛物线（图3-23中AB段）。即当接近布里渊区边界时，ε随k增加较慢，因此状态密度增高较多。在这个范围内，ρ（ε）-ε曲线位于抛物线之上。当这个变形的球继续增大，并终于在最近点碰到布里渊区边界时，ρ（ε）曲线达到最高点B（对应图3-22中a点对应能量，即图3-23中a点能量）。在这以后，只有布里渊区的角落高能量部分可以充填电子，由于角落部分的状态数少，因此状态密度降低。对无能带重叠（有禁带）的情况，当布里渊区完全填满时，曲线到达c，ρ（ε）降为0。c代表第一带最后一条曲线的顶部（图3-22a）。当第一布里渊区填满后，再充填下一个电子状态a′（图3-22中a′点对应能量，即图3-23中a′点能量），能量将有个陡增。这时出现了图3-23禁带ca′。此时，再增加电子将充填第二布里渊区（图3-23中a′C），这时要求具有更高的能量。

第二种是布里渊区产生重迭的情况（参见图3-22b）。其能态密度曲线如图3-24。进入第一布里渊区最初的电子和上述情况一样。当充填状态的费米面到达第一布里渊区的边界时，在A点发生陡降。当到达图3-24中的a′点对应的能量时，电子开始进入第二布里渊区。从图3-22b中可看到a′相当于第二布里渊区的最低能量状态。因为第一布里渊区c状态的能量高于第二布里渊区的a′状态的能量，当继续充填更多电子时，它们充填第一布里渊区的剩余状态和第二布里渊区的低能状态，在ρ（ε）-ε曲线上ρ（ε）表示的是两个重叠区纵坐标的和，如图3-24中BCD所示。所以ρ（ε）-ε曲线在a′到c之间突然升高。到达c点对应的能量时，第一布里渊区完全填满。以后的电子继续充填第二布里渊区。如果第二布里渊区和第三布里渊区重叠，也产生同样的效应，在ρ（ε）-ε曲线上有一系列的峰谷，其形状取决于晶体结构和区域之间能隙大小。

图3-23无能带重叠（有禁带）ρ（ε）-ε曲线

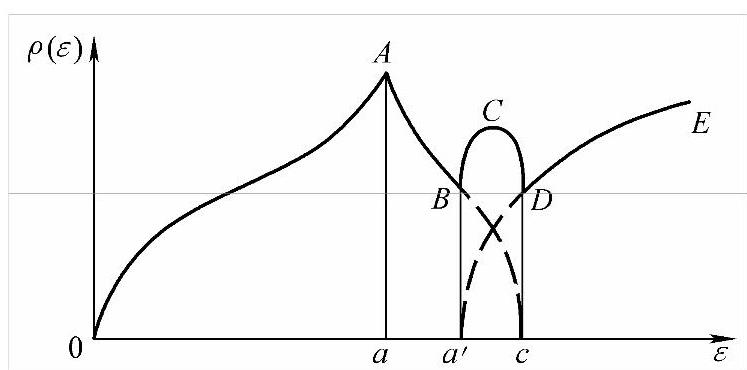
图3-24 有能带重叠（无禁带）ρ（ε）-ε曲线

用长波（波长约在100Å（10nm））X线谱法（软X线谱）可以测定金属及合金在费米能以下的ρ（ε）-ε曲线，这是一种研究金属及合金电子结构的方法。

（4）费密面

金属中的电子自低能级排起，直到全部价电子占据了相应的能级为止。在0K时低于费密能ε_F（0）的能级全被电子填满，高于费密能ε_F（0）的能级全空着。如果与ε_F（0）相对应的波数为k_F，对于自由电子来说，以k_F为半径的球体内填满电子，球外均为空能级，这个球的表面称为费密面。对于在晶体周期势场作用下的准自由电子来说，其费密面有些不是球面，而呈各种复杂的多面体的外形轮廓。对于简单立方金属，当电子少时，电子排布在第一布里渊区的原点附近，此时费密面为球面；但当电子逐步增多，电子在k空间的排布已接近布里渊区边界时，此时ε-k面已偏离球面而向外凸出，成为一个多面体。在与布里渊区边界相交时，费密面的变形更为显著。

对于具有体心立方晶体结构的碱金属，如Li、Na和K等，它们的价带是半满的，费密面距布里渊区边界还较远，因此这些金属的费密面是个球面。而具有面心立方晶体结构的贵金属，如Cu、Ag、Au等，其价带虽为半满，但沿[111]方向的费密面离布里渊区边界较近，因而发生强烈变形。

费密面这个概念的建立，其意义在于对固体的若干物理现象的理解。如导电，导热、热容，霍尔效应等均与费密面的概念有密切关系。即实际参加物理过程的电子并不是所有价电子，而只是靠近费密面附近的那些电子才是物理过程参加者，因此研究这些物理现象时，就要重点考查费密面附近电子的行为。