布洛赫定律：含周期势的薛定谔方程解析方法

如图3-10a所示，以周期a排列的N个原子构成长度为L的一维晶体周期势场V（x），在V（x）作用下的电子波动方程为

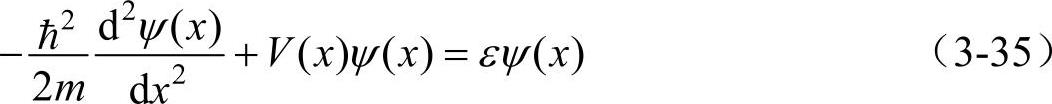
因为势场V（x）和晶体具有相同的周期，所以

V（x+a）=V（x） （3-36）

把一维晶体左右无限地连接起来或者把它的两端连接成环行，引入波函数的周期性边界条件

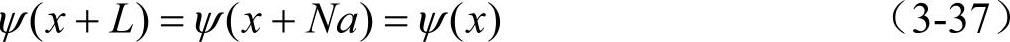
将式（3-35）中的x变换为x+a，则有

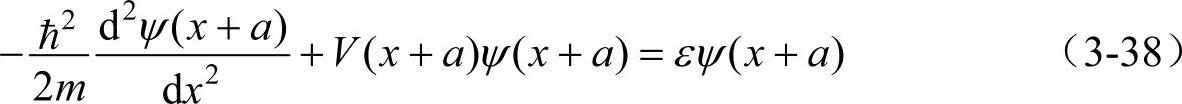
考虑到式（3-36）的条件，把式（3-38）和式（3-35）相比较，可以看出ψ（x）和ψ（x+a）是属于同一波动方程的同一本征值的两个本征函数，因此如果能量状态不简并（简并时也能证明得到下面的同样结果），则ψ（x）和ψ（x+a）线性相关，它们之间只差一个系数，即

ψ（x+a）=λψ（x） （3-39）

对坐标x重复进行N次长度为a的平移操作，则由式（3-39）得

ψ（x+L）=ψ（x+Na）=λ^Nψ（x） （3-40）

根据式（3-37）和式（3-40），则λ^N=1，即λ为1的N次方根。λ可表示为

式中，g是0≤g≤N-1区间中的整数。

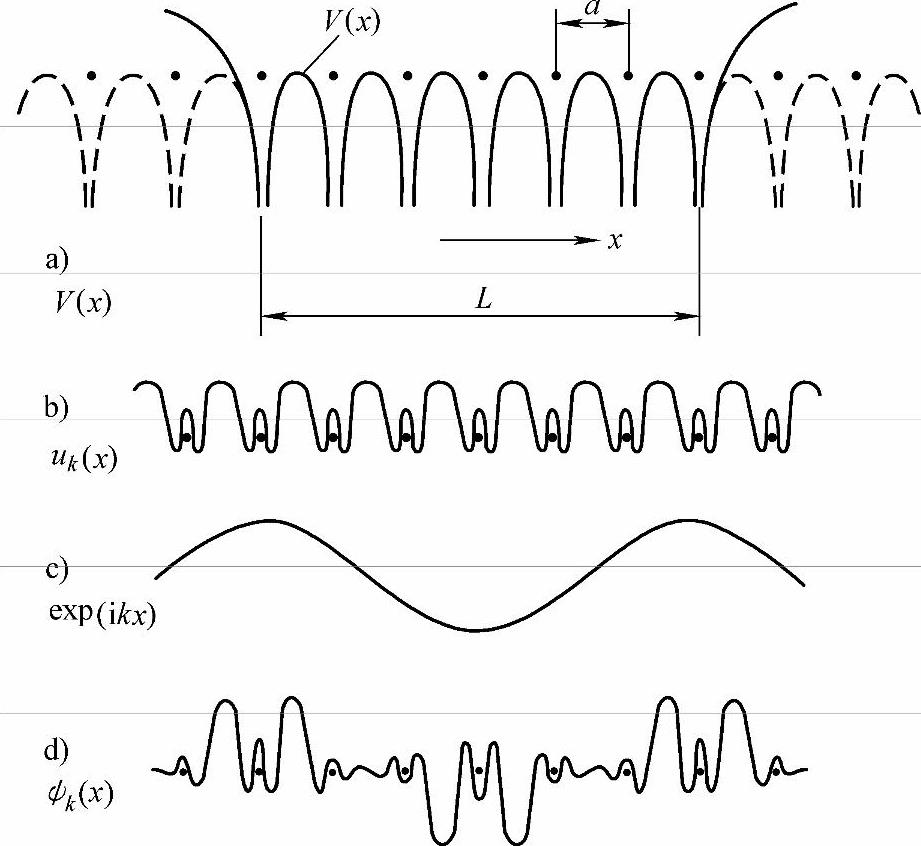
图3-10 布洛赫函数的周期性(www.xing528.com)

a）一维晶体的周期势场 b）与晶格有相同周期函数u_k（x） c）自由电子的平面波exp（ikx） d）布洛赫函数ψk（x）

因此式（3-39）可写为

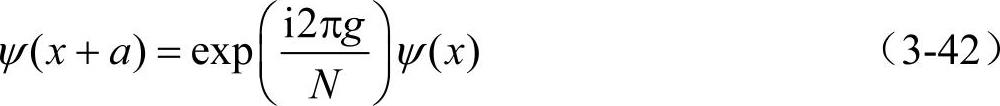
将式（3-42）两边同乘exp[-i2π（x+a）/（Na）]得

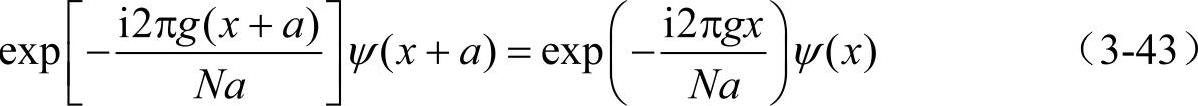
令

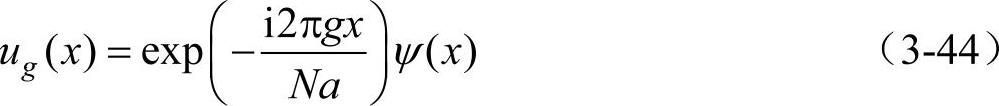
由式（3-43）可以看出，u_g（x）是具有和晶格势场有相同周期a的周期函数，如图3_-10b所示。根据式（3-44），在周期势场作用下的运动电子波函数ψ（x）可表示为

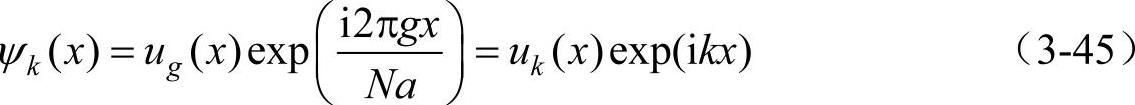
式中波数k=2πg/（Na）。式（3-45）称为布洛赫函数，布洛赫函数ψk（x）是由与周期势场有相同周期的函数u_k（x）调制的平面波exp（ikx）（自由电子的波函数），如图3_-10d所示。式（3-45）中脚标k表示波函数ψ（x）是由分立的波数k确定的。布洛赫函数ψk（x）具有下面的性质

ψ_k（x+a）=exp（ika）u_k（x） （3-46）

从波数k的定义k=2πg/（Na）=2πg/L可以看出，k许可的值是分立的，和一维势阱中的自由电子的情况一样，这些值在k轴上以2π/L的间隔排列着。

把一维布洛赫函数推广到三维时，采用波矢k（k_x，k_y，k_z）和位置矢量r（x，y，z），则三维布洛赫函数为

ψk（r）=u_k（r）exp（ikr） （3-47）

布洛赫证明了一条重要定理，即对于含周期势的薛定谔方程，其解必定具有布洛赫函数的形式。