三维自由电子模型优化

1.费米半径和费米能

边长为L的立方体晶体块，其内部的电子可以看成三维有限势阱内的电子。根据式（3-22），在波矢k空间（以k_x、k_y、k_z为坐标建立的波数空间）中，等能面（ε_k为常数）为球面，如图3-5所示。k_x、k_y和k_z均可以取正值、负值和零。电子的能量与k²成正比。由式（3-22）可知，具有相同的k²值的点具有相同的能量，例如（2π/L，0，0）、（0，2π/L，0）和（0，0，2π/L）坐标点的能量值相等，却表示不同的量子状态（量子状态不同于能量状态），电子由靠近原点低能量状态依次填充到更高的能量状态。设有N个电子占据了从原点到半径k=k_F的球面（称为费米球）之间的能量状态。k空间放大时，k空间中每一个微小体积（2π/L）3就有一个量子状态，考虑到电子的自旋，一个量子状态可以容纳两个电子。半径为k_F的球的体积为（4/3）πk_F³，因此有

因此费米球半径k_F为

式中体积V=L³。费米面上的电子速度（费米速度）ν_F为

根据式（3-22），费米球表面处的能量（费米能）ε_F为

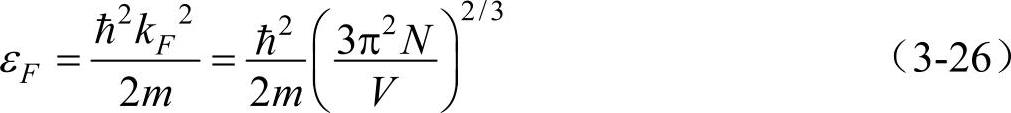
普通金属中ε_F约为5eV，ν_F大约为1.5×10¹⁶m/s。

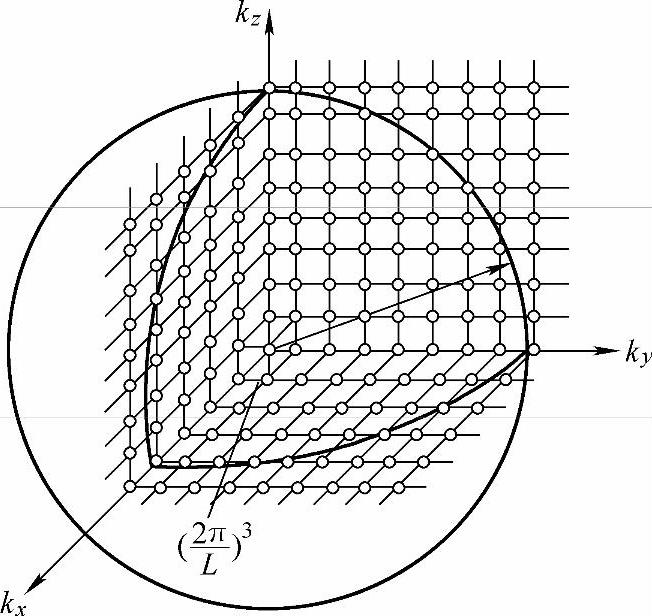
图3-5 三维自由电子的能量状态和费米球

2.费米—狄拉克统计和靠近费米能级的能量

电子数的能量分布情况可用状态密度来描述。状态密度就是晶体内单位能量间隔的状态数（即电子数），用ρ（ε）表示。如图3-6所示，在k空间中，由能量ε到ε+dε的两个等能面所包围区域的体积为4πk²dk，每一个微小体积（2π/L）3就有一个量子状态，所以考虑到自旋并利用式（3-22），得到三维情况下的状态（不是能量状态）密度函数ρ（ε）为

即(www.xing528.com)

ρ（ε）与ε呈抛物线关系。在T=0K时，电子最大的能量为ε_F（0）（0K时的费米能），在ε_F（0）以上，各态均无电子，在ε_F（0）以下各态均填满电子，而且愈接近ε_F（0）其状态密度愈大，如图3-7a所示。

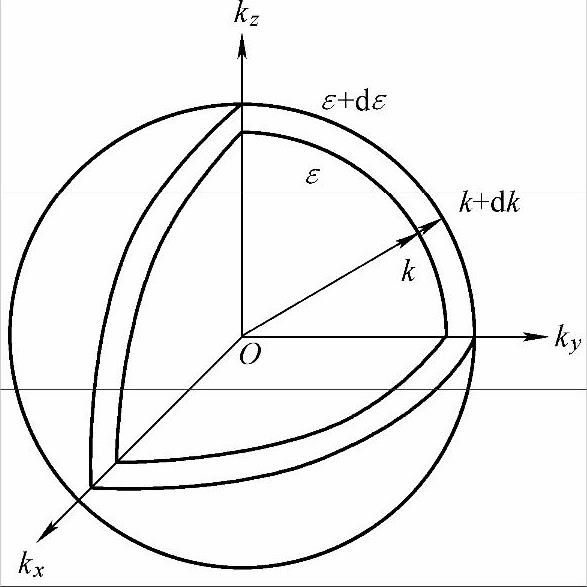
图3-6 三维自由电子的等能面

在任意温度T（单位为K）时，热平衡状态下，电子处于能量为ε的几率，可用费米—狄拉克分布函数描述。由于电子比一般气体分子轻很多，金属中电子密度比标准条件下一般气体分子高10⁴倍，电子的能量变化是量子化的，因此对金属中的电子，经典力学范畴的麦克斯韦—玻耳兹曼统计已不合适，需用量子统计，或称费米—狄拉克分布（或统计）。该统计的基本假设是：电子彼此不能区分；一个能带的每一个能级最多只能被两个自旋相反的电子占据。该统计的关系式为

式中f（ε）为费米—狄拉克分布函数，它表示在热平衡时，电子处于能量为ε的几率；ε_F为温度为T时的费米能；这里的k为玻尔兹曼常数。分布函数f具有下列性质：当T=0K时，若ε＞ε_F（0），f=0；若ε＜ε_F（0），f=1，如图3-7b实线所示。就是说为了使系统总能量最小，电子倾向于占有能量低的状态，能量小于ε_F（0）的状态均被电子占有；能量大于ε_F（0）的状态全部空着。当T>0K，f的分布如图3-7b中虚线所示，若ε=ε_F，f=1/2（在图3-7b中，视ε_F≈ε_F（0））。在室温下kT≈0.025eV，而金属的ε_F为几电子伏特。因此只有少量和能量ε_F接近的电子能吸收热能而跃迁到能量较高的状态，故高于ε_F的原来空的能态也有部分被电子占据。能量比ε_F低更多的电子不能吸收热能，因为kT能量不足以把这些电子激发到更高能级，而相近的能级则已被电子填满。这是量子力学处理电子分布问题所得出的崭新的概念。

可以导出在0K时电子的平均动能为（3/5）ε_F（0），说明在绝对零度，电子仍然具有相当大的平均动能。这也是与经典理论截然不同的概念。

当T＞0K，且kT＜ε_F（F）时，有

由式（3-30）可见，当温度升高时，ε_F（F）要从ε_F（0）下降。但因kT》ε_F（0），所以直到金属处于熔化状态的温度时，ε_F与ε_F（0）相差很小，故可以把费米能看作一个常数。

在温度不为零时，电子的状态密度分布如图3-7c所示。在ε_F周围大约2kT的范围内，电子占据情况变成虚线的样子。

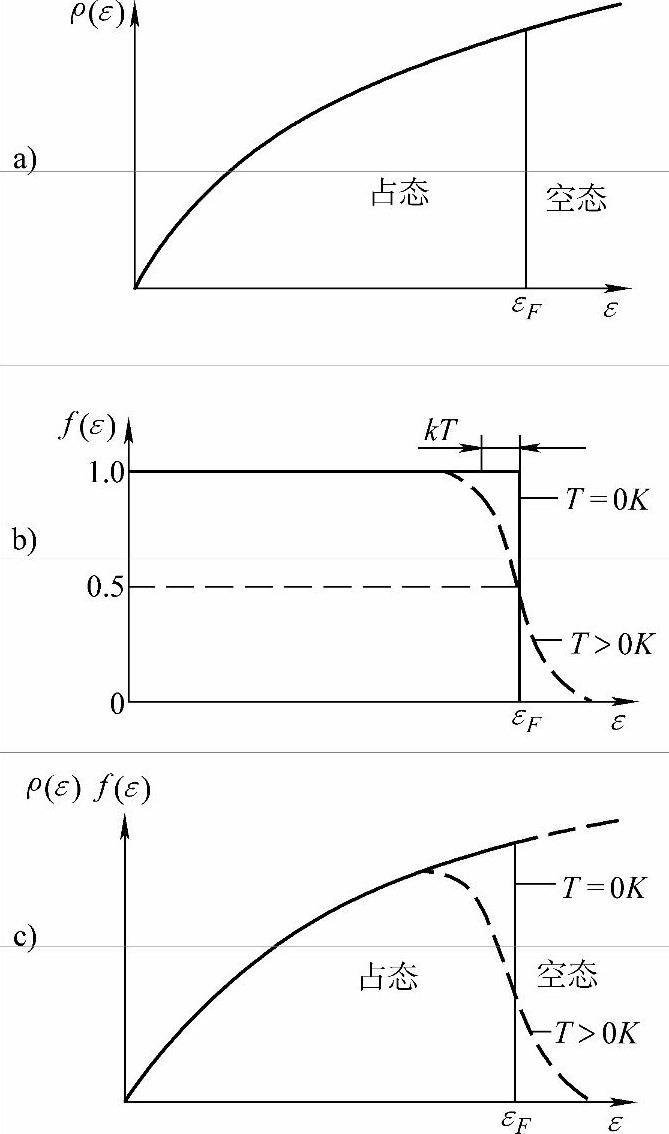
图3-7 靠近费米能级时电子状态分配特点

a）0K时状态密度曲线 b）电子状态几率分布曲线 c）几率分布对电子状态分配的影响