阱内势能为零的电子状态分析

1.一维势阱

（1）一维无限深势阱

一个理想的势阱模型—无限深势阱。阱内（金属内）电子完全自由，只有动能，没有势能；阱外势能无限高，即

其势能曲线如图3-2所示。

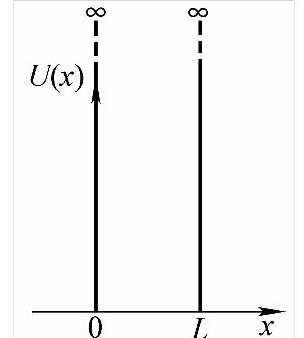
图3-2 一维无限深势阱

质量为m、能量为ε的自由电子被封闭在如图3-2所示的长度为L的一维势阱中。描述阱内电子运动的薛定谔方程为

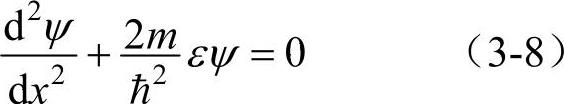
式中ћ为约化普朗克常数。令

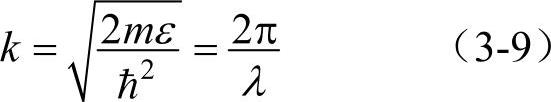
这里k就是波数。式（3-8）可改写为

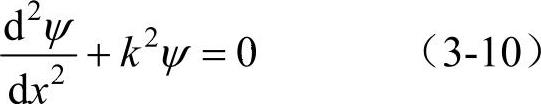
方程式（3-10）的解为

ψ（x）=Asin（kx+δ） （3-11）

因是无限深势阱，有边界条件ψ（0）=0和ψ（L）=0。将边界条件代入式（3-11）则有δ=0和sin（kL）=0，从而得到

kL=nπ（n=1，2，3…） （3-12a）

式（3-12a）中n=0时，ε=0，舍去此状态。式（3-11）中的常数A可根据0～L区间的波函数归一化条件求出，归一化条件为

求出的A值为（2/L）1/2。将δ和A值以及式（3-12b）代入式（3-10）得

将式（3-12a）代入式（3-9）得

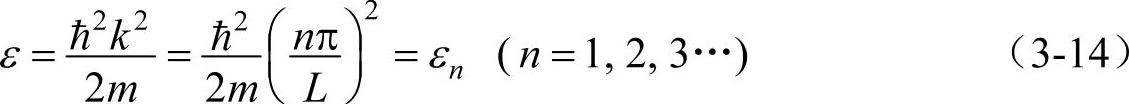
式（3-14）表明金属中的电子所有的能量是量子化的，有正整数n确定，n叫量子数。图3-3是处于势阱中电子的波函数及波函数的平方。由图3-3可见，在不同部位找到电子的几率是不同的。

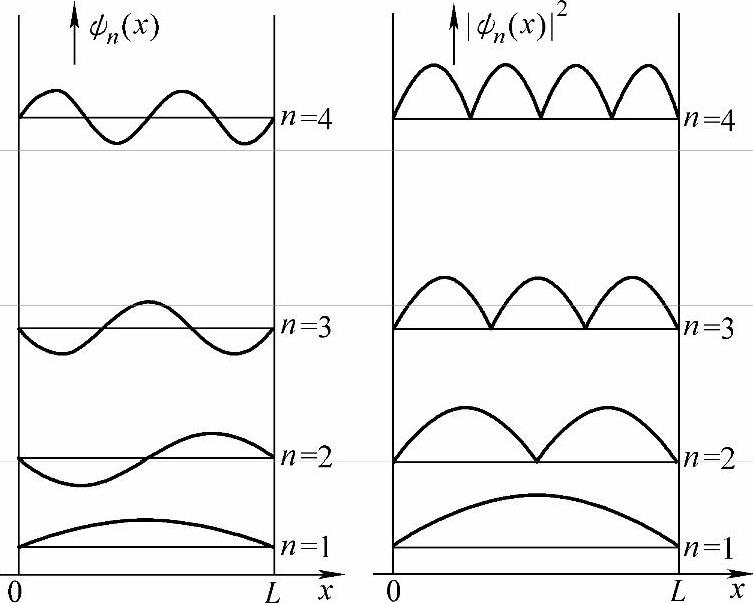
图3-3 处于势阱中电子的波函数及波函数的平方(www.xing528.com)

（2）一维有限深势阱

实际金属表面势垒的高度是有限的（宽度也较小），所以在x=0和x=L处的边界条件不容易确定，为此，假定波函数ψ（x）具有长度为L的周期，如图3-4a所示。于是，边界条件为

ψ（x）=ψ（x+L） （3-15）

这个边界条件相当于把长度为L的一维势场两端连接成如图3-4b所示的环形，并假定波函数ψ（x）具有长度为L的周期。这个假定完全是一种数学技巧，其目的是避开具体假定边界条件的困难。由于固体内部的性质不受表面的影响，因此这样处理是允许的。对波函数假定的条件式（3-15）称为周期性边界条件。

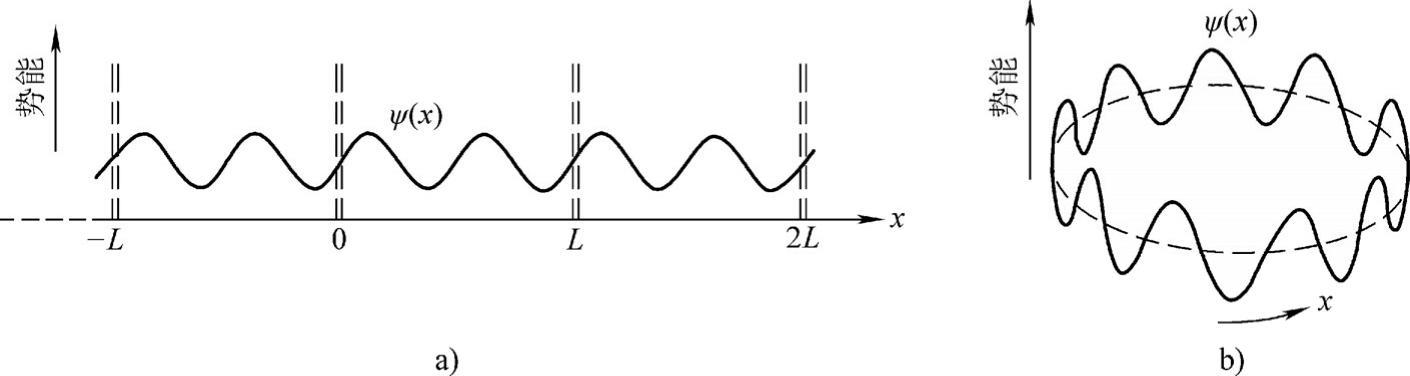
图3-4 周期性边界条件

a）周期波函数 b）环形周期波函数

势阱内的波函数和解也分别是式（3-10）和式（3-11）。将周期性边界条件式（3-15）代入式（3-11）可得kL=2nπ，n为正整数（n=0舍去），即

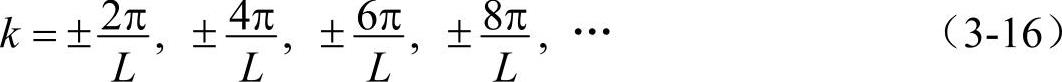
将式（3-16）代入式（3-9）得

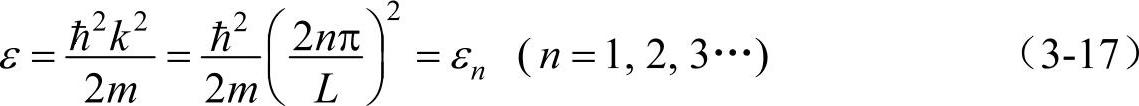
由式（3-17）可以看出，ε与k为抛物线关系，在k轴上，每个能量状态所占长度为2π/L。波函数中的δ和A值无法求得。

2.三维有限势阱

上面讨论了一维有限深势阱，现在讨论封闭在边长为L的立方势箱（有限势阱）中质量为m、势能为ε的电子运动状态。设波矢为k，方向与电子运动方向相同，k=2π/λ=（2mε/ħ²）1/2。波动方程为

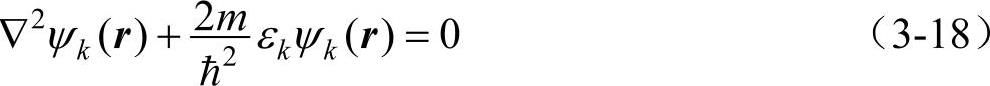
其波函数为

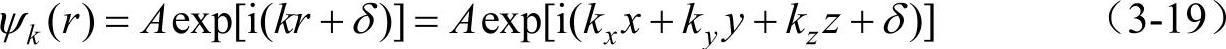
波函数和能量的脚标k表示状态是由波矢k决定的。

和一维的情况一样，假设x、y、z各方向具有周期性的边界条件为

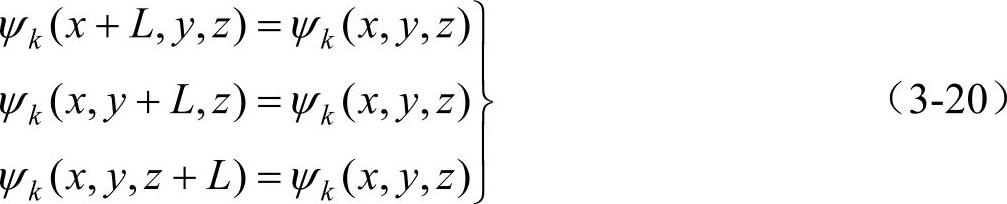
式中k²=k_x²+k_y²+k_z²。将式（3-20）代入式（3-19）得所允许的波矢k的三个分量为

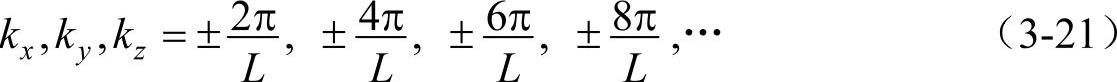
本征能量值ε_k为

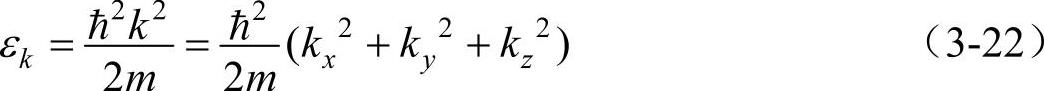
对于k_x、ky、kz，每隔2π/L有一个量子状态，波矢k的三个分量的值决定后，能量状态ε_k就决定了。