原子间作用力及其来源：探究原子力学中的关键问题

1.原子间的作用力

两个原子间的化学亲和力，从物理本质上说，是由于在这两个原子之间存在吸引力。然而即使在化学亲和力很强的情况下，原子也难以过于接近，因为当原子相距很近时，它们之间主要显示排斥力。这种排斥力是一种短程力，即在远距离处它的数值很小，但在近距离处它比吸引力大。在平衡状态时，原子间的吸引力和排斥力相等。这时两个原子间的距离即为平衡距离。物体所受的合力为势能随距离的改变率。因此，原子在平衡距离处的势能具有极小值。

一个材料内部的势能等于每个原子的能量及相互作用能量的和。势能的零点可以任选，令原子相距很远，都处于基态，相互没有作用时，其势能U=0。那么要形成一个固体，必须把这些原子从远处移到一起，假如所形成的原子集团，要比原来分散的原子更稳定，则其势能必须小于零，就是说总的相互作用能必须是负值。由于原子在吸引时做功，所以吸引的势能U_a是负值，它是原子间距离r的幂函数。U_a=-α/rⁿ，α为正的比例常数。当距离很远时，U_a=0，以后随距离缩短而U_a绝对值减小，如图2-8a最下面的虚线所示。相反，排斥的势能U_r是正值，要把互相排斥的原子聚在一起，外界必须对它做功。U_r的大小也是原子间距离r的幂函数幂。U_r=β/r^m，如图2-8a上面虚线所示，β也为正的比例常数。当r减小到一定程度时，U_r急剧增加，致使U_r比U_a变化得更快。总的势能U是该两项值的和，即

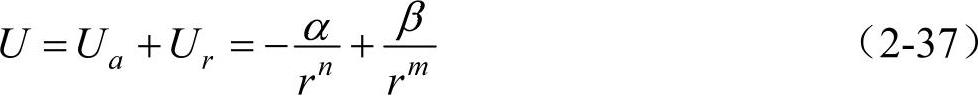
U在图2-8a中以实线表示。

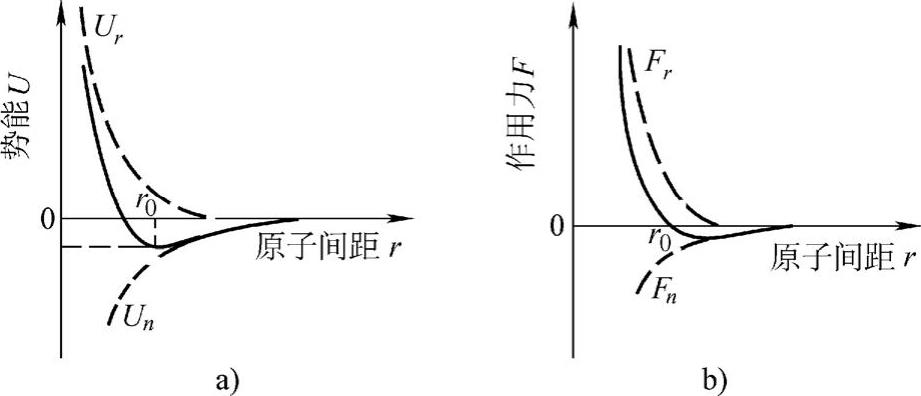
图2-8 势能及作用力与原子间距离关系

a）势能曲线 b）作用力曲线

原子间的作用力F（r）可由式（2-37）微分导出

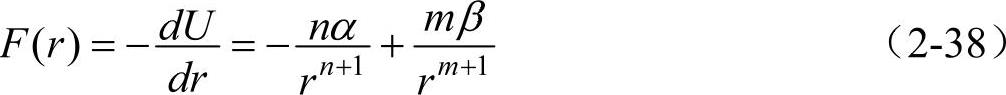
式中，m>n，负项为引力F_a；正项为斥力F_r，见图2-8b。当达到平衡间距r₀时，吸引力和排斥力平衡，即F（r₀）=0，则

r=r₀时，原子集团的势能具有最低值，即在图2-8a中如果增加或减小原子间距离，都使势能增加，原子集团变得不稳定。对于某些离子晶体，n=1，m=9；对于某些金属，n=1，m=3；对于其他类型的晶体，n和m又有不同的数值。

可以设想固体的一个分子是这样的：在它中间有两个以上的原子核，外面绕有负电荷的电子云，靠静电引力结合起来。其结合强度取决于原子核之间各点的电子云密度。(www.xing528.com)

2.原子间作用力的由来当原子由远处移近时，在原子之间产生引力。在原子间距达到几个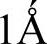（=0.1nm）时，产生了平衡引力的斥力。斥力的产生最主要是由于原子核外面的电子云有了重叠。当两个电子壳层开始重叠时，每一壳层中的电子都不能再认为是仅属于其原来的原子了，而为分子整体所共有。在这些壳层中的电子的运动和能量仍然遵守量子规律，特别是不相容原理。如果这两个电子壳层原来都是填满的，那么当它们结合成一个统一的电子集团时，不能保证所有的电子都占据低能量的量子状态，其中有些电子就要攀登到较高的能级。这种能量的增加就引起了斥力。满壳层重叠时必然导致上述的斥力。在价电子的电子云没有重叠以前，中性原子间不会有很强的化学结合力。

当两个原子相互移近时，距原子核最远的价电子比其他电子更早发生重叠，因为价电子只占据部分填充的壳层，当它们重叠时就会产生引力。但是，当两个原子满壳层的电子云也发生重叠时，就会出现满壳层间的斥力。

价电子重叠所产生的引力，可以用氢分子的形成来说明。氢分子由两个质子和两个电子所组成。在分析电子的运动时，质子可以认为是静止的，其作用力主要考虑粒子之间最强的静电力。如果这些粒子之间的力要形成化学键，则两个电子必须把大部分时间用在两个核之间。当两个电子互相接近时，它们之间的斥力是大的；但同时，由于这两个电子同时接近两个质子，因而产生四个引力，这四个引力足够抵消上述斥力。用量子力学处理这个问题，可以知道电子在分子的各个地方运动所用去的时间，从而计算出这四个粒子之间静电力的平均值。如果电子把大部分时间用在分子中的某个地方，那么，在计算平均作用能量时，这个地方的电子与其他粒子作用的能量就较大。

电子在分子中的分布是遵守量子力学规律的。假定最初原子相距很远，相互间没有作用，这时每个原子有一个电子处于（1s）状态。这个状态的波函数是一个以原子核为中心的球形分布的电子云。电子云密度随其与原子核的距离的增加而急剧减小。如把两个原子彼此移近，使它们的电子云恰好有不大的重叠，那么这时电子运动的特点是，电子能够从一个原子跑到另一个原子上去，而且不可能区分哪个电子是属于哪个原子。这样就改变了原来的波函数，原来是两个（1s）函数，现在需要用新的波函数来表示电子在分子整体中的运动。假设两个（1s）电子云开始重叠时没有什么变化，那么就有两个不同的（1s）型的ψ函数，以原子核a为中心有ψ_a，以原子核b为中心有ψb。两个电子用1和2表示，并且以ψ_a1表示电子1处于ψ_a的量子状态。这样，在分子中某点P的ψ_a1²表示当电子1处于原子核a的1s状态时，它在P点出现的几率。同样，ψb2²表示当电子2处于原子核b的（1s）状态时，它在某点Q出现的几率。因此，当电子2在Q点时，在P点找到电子1的几率为它们两者几率的乘积ψ_a1²ψb2²，这称为两者的合成几率。这就有可能把ψ_a1ψb2看作是两个电子的总的波函数。也可设想电子2在P点有波函数ψ_a2，电子1在Q点有波函数ψb1，那么就得到总的波函数为ψ_a2ψb1。显然，以上得到的两个波函数没有一个能单独满足要求，因为每个电子都能从一个原子移往另一个原子，并不能区分那个电子是属于那个原子的。我们所能知道的，只是当一个电子在Q点时，另一个电子在P点出现的几率，因此ψ_a1ψb2与ψ_a2ψb1必须有相同的机会出现。波函数的性质之一是可以把已知的波函数相加得出新的波函数。对于薛定谔方程来说，已知解的线性组合，仍为其解。因此得出新的波函数ψ+和ψ-为

在ψ+中把标号1和2互换，不改变波函数；在ψ-中交换1和2的标号，则ψ-为负值。所以ψ+是一个对称的波函数，而ψ-是一个反对称的波函数。

相应于式（2-40）和式（2-41）波函数的合成几率为

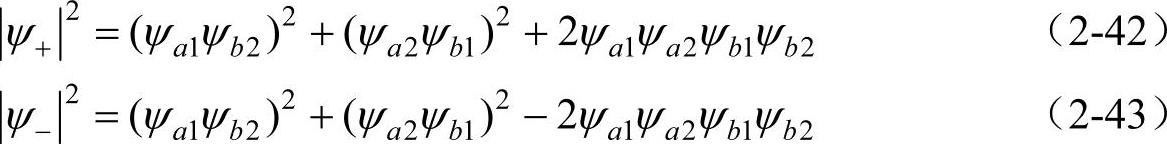
在式（2-42）和式（2-43）中，前两项的四个ψ函数是描述一个电子围绕一个原子核处于（1s）状态运动的波函数，它们的数值在两个原子核的中心处大致是相等的。两个方程的最后一项代表两个原子的交换作用，这是因为它们有交换各自电子的可能性。交换作用对分子能量的贡献通常称为交换能。所以在两个原子核的中心处│ψ+│²的值很大，而│ψ-│²等于零。因此ψ+所表示的是电子在分子中以大部分时间用在原子核之间，并且把它们联结在一起，形成一个稳定分子的量子状态；而ψ-则表示电子避开这个中心区域，不能形成结合键的一个状态。原来的（1s）能级就分裂成如图2-9所示的两个能级ε_A（r）及ε_s（r）。其中ε_s（r）这个能级属于ψ+，ε_s（r）曲线在r=0.87Å（0.087nm）处有一个能量最低点，说明两个氢原子接近到这种程度时可以形成稳定的H₂分子，这就是结合状态（图中虚线为实验测定值），这时它们的两个电子是自旋相反的。当两个氢原子相互接近时，如果它们的电子自旋是平行的，那么原子间的相互作用永远是排斥的，如图2-9中ε_A（r）曲线，不能形成稳定的分子。ε_A（r）这个能级属于ψ-。

上面用氢原子价电子重叠形成氢分子解释了原子作用力的由来。这个原理同样可以用来说明金属理论中的一些问题。例如两个氢原子彼此接近时，1s能级分裂为两个能级的情况与金属价电子能级展宽是很相似的。氢分子只有两个氢原子，1s只能分裂成两个能级；而在金属晶体中，每立方厘米体积中具有10²³数量级个原子，因此可分裂成间隔很小数量很多的能级，称为能带，但它们的本质过程是一样的。

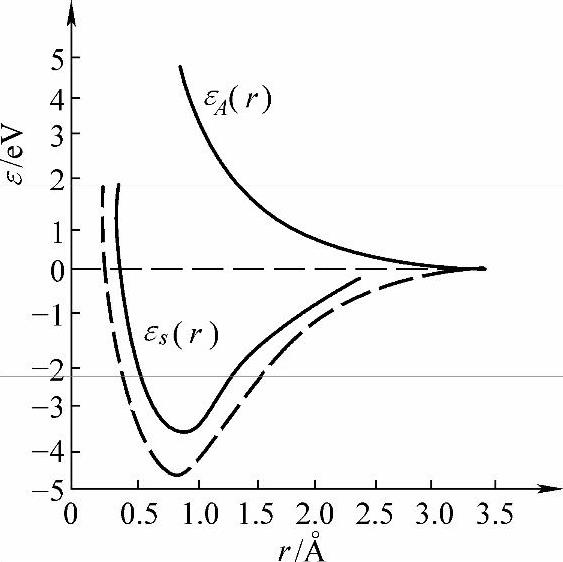
图2-9 氢分子1s能级分裂