玻色分布和费米分布的区别与应用

对玻色系统中的微观状态（热力学概率）公式（1-113）两边取自然对数，得

假设a_l》1，ωl》1，因而al+ωl-1≈al+ωl，ωl-1≈ωl，并根据斯特令公式（1-116），式（1-126）可化为（将Ω_B.E.简记为Ω）

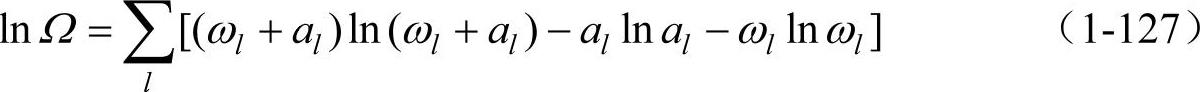
类似玻尔兹曼分布的求法，可求得

式（1-128）给出玻色系统中粒子的最概然分布，称为玻色—爱因斯坦分布或玻色分布。

对费米系统中的微观状态（热力学概率）公式（1-114）两边取自然对数，得

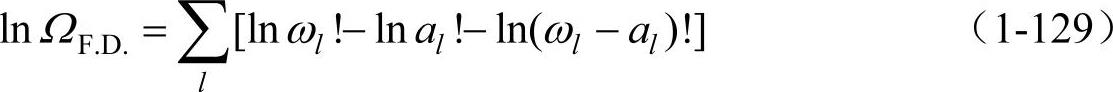
假设a_l》1，ωl》1，ωl-al》1，式（1-129）可近似为（将Ω_B.E.简记为Ω）

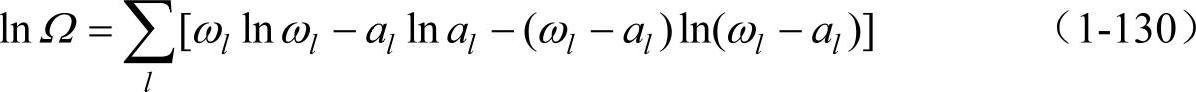
可求得(www.xing528.com)

式（1-131）给出费米系统中粒子的最概然分布，称为费米—狄拉克分布或费米分布。

式（1-128）和式（1-131）分别给出玻色系统和费米系统在最概然分布下处在能级ε_l的粒子数。能级ε_l有ω_l个量子态，处在其中任何一个量子态的平均粒子数应该是相同的。因为a_l/ω_l是能量为ε_l的一个量子状态被粒子填充的几率，所以它就是占有率ƒ（ε_l）。另外β还可以热力学定义求得，由热力学定义可求得β=1/（kT），并设α=-ζ/（kT），k即玻尔兹曼常数。则有

正号为费米—狄拉克分布，负号为玻色—爱因斯坦分布。

图1-24示出了费米—狄拉克统计的分布函数，系统常数ζ称为费米能级。在T→0的低温下，能量小于ζ的所有能级都被粒子填满，ƒ（ε）=1，能量大于ζ的所有能级都完全没有粒子，ƒ（ε）=0。随着温度的升高，如图1-24所示，粒子分布的界线逐渐模糊起来。

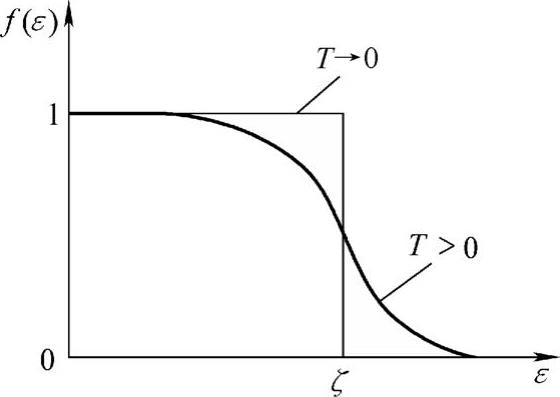
图1-24 费米—狄拉克分布

无论是玻色—爱因斯坦分布还是费米—狄拉克分布，在能量很高（ε-ζ》kT）时，粒子的分布都近似等于麦克斯韦—玻尔兹曼分布。

在粒子可以分辨的假设下导出玻尔兹曼分布。自然界中有些系统可以看作由定域的粒子组成，例如晶体中的原子或离子定域在其平衡位置附近作微振动，这些粒子虽然就其量子本性来说是不可分辨的，但可以根据其位置而加以区分。在这意义下可以将定域粒子看作可以分辨的粒子。因此由定域粒子组成的系统（称为定域系统）遵从玻尔兹曼分布。定域系统和满足经典极限条件的玻色（费米）系统虽然遵从同样的分布，但它们的微观状态数是不同的。