1.叠加原理
现在令Ψ1和Ψ2满足波动方程式(1-49)。如果c1、c2为常数,若Ψ=c1Ψ1+c2Ψ2,很容易证明Ψ也满足式(1-49)的波动方程。再进一步,若Ψ1、Ψ2、Ψ2、…、Ψn分别为波动方程的解时,那么它们的线性组合

也为波动方程式的解。式中ci是常数。这就叫做叠加原理,是波动现象的特征之一。光和声波的干涉和衍射现象就是由于波的叠加产生的。
波函数绝对值的平方表示波的强度,如果利用式(1-73)则有
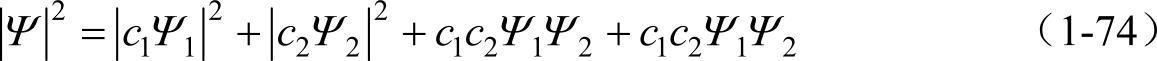
合成波的强度不等于各自分波强度的简单相加,而是多出两个分波的函数的乘积项。此项就是干涉项。干涉项根据两个波函数的位相差,它的值从正到负有较大的变化。
2.两简谐波叠加形成的波包
现在考察两个频率相近、振幅相同、同方向传播的简谐波的叠加。设两个波的波动表达式为

为了简单起见,假设它们在原点的初相位相等且为零(这里A即为振幅,与上面不同)。其合成波为
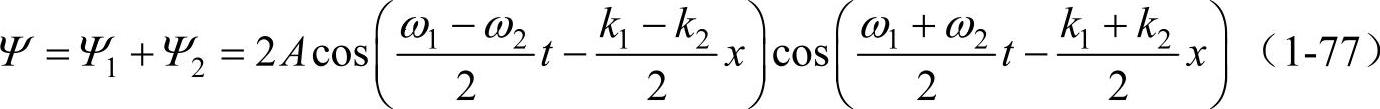
合成的结果如图1-18所示。图中上图表示频率稍有不同的两列波,下图表示合成波(合成波振幅(虚线)随时间作周期性地变化)。由于Δω=ω1-ω2《ω1或ω2,Δk=k1-k2《k1或k2,所以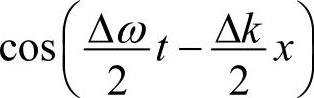 变化缓慢,如虚线所示的包络线;而
变化缓慢,如虚线所示的包络线;而 则表示一个小的波形。如果令
则表示一个小的波形。如果令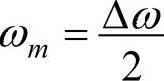 ,
,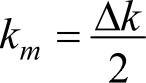 ,
, ,
, ,则式(1-77)可写为
,则式(1-77)可写为

可以把式(1-78)看成是一个角频率为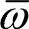 、波数为k的波,这个波的速度为
、波数为k的波,这个波的速度为

它的振幅Am(x,t)随时间和位置作比较缓慢的周期性变化。显然,这个变化的振幅Am(x,t)本身也具有沿x方向传播的简谐波的形式(如图1-19所示),它的角频率和波数分别为ωm和km,而传播速度为

通常称这样的振幅为调制的振幅。(https://www.xing528.com)

图1-18 波包
这样,两个频率相近、等振幅的简谐波叠加的结果是一个振幅缓慢变化的波,它的角频率为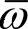 、波数为
、波数为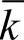 ,波速为
,波速为 。它的振幅的变化也像一个传播的波,它的角频率为Δω/2,波数为Δk/2,波速u=Δω/Δk。这样的合成波称为波包。波包有g两个速度,up称为它的相速度,ug称为它的群速度(在图1-19中箭头以群速度ug行进,白圈以相速度up行进)。群速度在研究光的散射以及微观粒子波动性等问题都是很重要的概念。
。它的振幅的变化也像一个传播的波,它的角频率为Δω/2,波数为Δk/2,波速u=Δω/Δk。这样的合成波称为波包。波包有g两个速度,up称为它的相速度,ug称为它的群速度(在图1-19中箭头以群速度ug行进,白圈以相速度up行进)。群速度在研究光的散射以及微观粒子波动性等问题都是很重要的概念。

图1-19 波包相速度和群速度
3.两简谐波叠加形成的驻波
驻波是一种波形不向前传播的波,波形向前传播的波称之为行波。驻波是干涉的特例。在同一媒质中两列振幅相同的相干波(即振幅|A|、角频率ω、波长λ均相同),在同一直线上沿相反方向传播时就叠加形成驻波。设有两列振幅相同的相干波分别沿x轴正方向和负方向传播,在两波中各选一个波峰,取两波相遇时t=0,且x=0,它们的表达式可写成
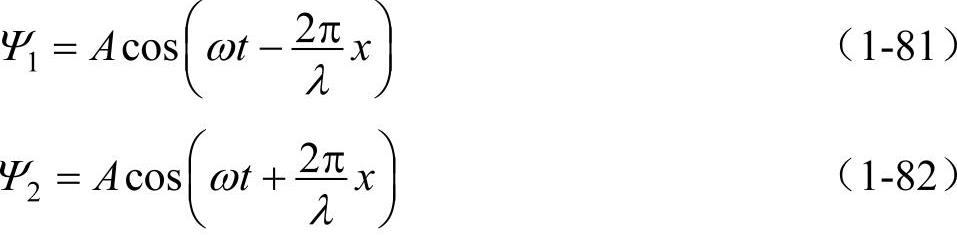
其合成波为
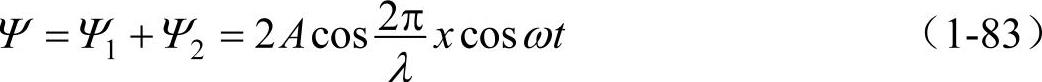
式(1-83)中的空间坐标和时间坐标分开,是驻波的典型表达式。由式(1-83)可以看出,合成以后各点都在做同频率的简谐振动,但各点的振幅为|2Acos(x2π/λ)|,即驻波的振幅与位置有关(与时间无关)。振幅最大发生在|cos(x2π/λ)|=1,即x2π/λ=kπ的各点,这些点称为波腹,它们的位置可由下式决定

亦即波腹在与原点距离为λ/2的整数倍的位置处。同样,振幅的最小值发生在|cos(x2π/λ)|=0,即x2π/λ=(2k+1)π/2的各点,这些点称为波节,它们的位置可由下式决定

亦即波节在与原点的距离为λ/4的奇数倍的位置处。由式(1-84)和式(1-85)可算出相邻的两个波节和相邻的两个波腹之间的距离都是λ/2。这一点为我们提供了一种测定波长的方法,只要测出相邻两波节或波腹之间的距离就可以确定原来两列行波的波长。
式(1-83)中的振动因子为cosωt,似乎驻波中各点的振动的相都是相同的。其实不然,因为系数2Acos(x2π/λ)在x的值不同时是有正有负的。把相邻两个波节之间的各点叫做一段,则由余弦函数取值的规律可知,cos(x2π/λ)的值对于同一段内的各点有相同的符号,对于分别在相邻两段内的两点则符号相反。以|2Acos(x2π/λ)|作为振幅,这种符号的相同或相反就表明,在驻波中,同一段上的各点的振动同相,而相邻两段中的各点的振动反相。因此,驻波实际上就是分段振动现象。图1-20画出了驻波形成的物理过程,其中虚线表示向右传播的波Ψ1的波形,点线表示向左传播的波Ψ2的波形,点划线代表虚线和点线重合时的波形,实线是合成波Ψ的波形。由图1-20可见,在各个波节处,两波在任一时刻的位移恰好相消,在波腹处,两波的位移相长。在同一段上驻波各点振动同相,相邻两段中的各点振动反相。

图1-20振幅相等、频率相同、传播方向相反的两列简谐波叠加而形成驻波
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




