波的基本方程式简述

在自然界里有声波、弹性波、电磁波等各种波动现象。所谓波动，就是以介质中的各点作为中心，振动在它的平衡位置上而在空间传播的现象。在广义的波动现象中，变化的量没有必要由平衡位置的变位来限定，一个物理量如果能随时间、空间变化，就是一种信息在空间的传播现象。因此，热传导现象也可以认为是波动现象。

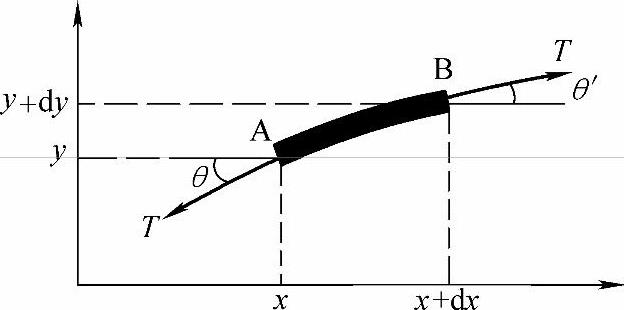
图1-15 弦的振动

假如ψ看作物理量时，给出ψ的空间的、时间的变化的微分方程式，叫作波动方程式。研究一下细弦的横向振动，就是一个简单的例子。如图1-15所示，试分析一下这个弦的很小一部分AB。设弦的张力为T，张力T在A点中的y分量为-Tsinθ，而B点是Tsinθ′。如果认为θ、θ′是很小的话，则用于AB部分的y分量合力dF为

dF=T（sinθ′-sinθ）≈T（tanθ′-tanθ） （1-45）

因为

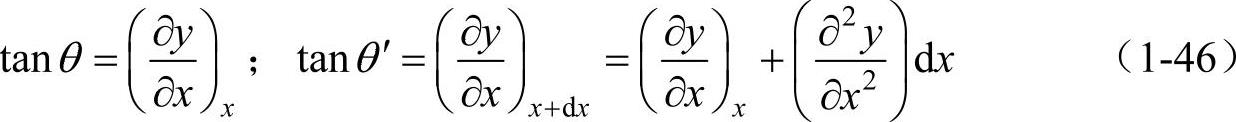
所以，由式（1-45）和式（1-46）可得

另一方面，AB部分的y方向加速度，如果用t表示时间，则以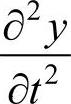

表示。设σ为弦的线密度时，质量为σdx，去掉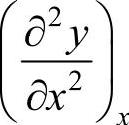的角标x，根据牛顿第二定律，则有

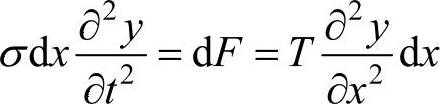
即(www.xing528.com)

这是关于弦横向变位y的时间t和x坐标的二阶偏微分方程式，这就是波动方程式。

以上是弦的横向振动，在一般情况下，波动方程式稍微复杂一点，如下面的二阶偏微方程式

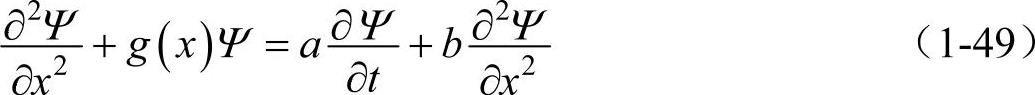
式中Ψ表示变化的物理量，是波函数的总称。如果Ψ是Ψ（x，y，z，t）的三维变化量时，波动方程式为

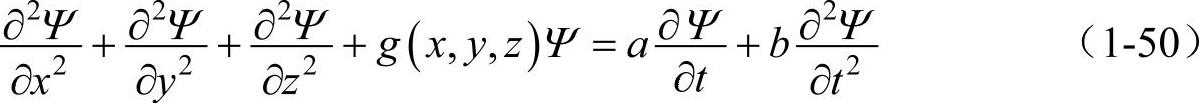
或者用下式表示

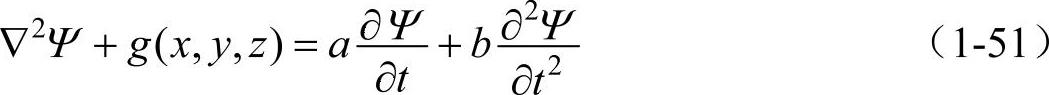
∇²是拉普拉斯算符。g（x，y，z）是在空间能够变化的系数；a、b是常数。例如，在麦克斯韦的电磁方程式中，设ε、μ、κ分别为介电常数、磁导率、电导率，则电场矢量E、磁场矢量H分别要满足波动方程式

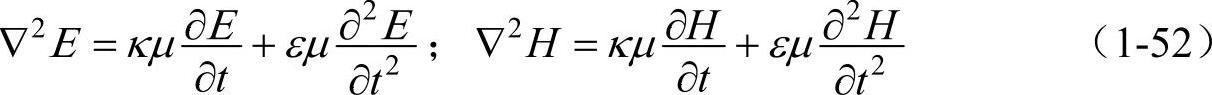
在这种情况下，Ψ为E或H；g=0；a=κμ；b=εμ。

根据式（1-50）或者式（1-51）完全可以求出波动现象，但得到什么样的解？这取决于Ψ的边界条件和起始条件。