探究量子世界的基石：薛定谔方程

薛定谔把玻尔原子系统的能级理论、德布罗意物质波思想以及哈密顿的经典力学与几何光学的数学相似性思想结合起来，形成了波动力学概念，建立了薛定谔方程。方程建立过程中一个突出特点就是善于运用物理类比。薛定谔通过力学与光学类比形成波动力学概念，通过几何光学与经典力学的相似性得出波动光学与波动力学的相似性，从而根据普遍的波动方程建立起了薛定谔方程。

1.波函数

具有能量E和动量p的自由运动的一个微观粒子必然表现出波动性，我们用波函数来描述它的运动状态。自由粒子不受力，动量p不变，能量E不变，所以同它联系的波长λ不变，频率ν不变，波的传播方向也不变，是平面单色波。我们知道，频率为ν、波长为λ沿x轴方向传播的平面单色波的可以用下式表示

将这个公式写成复数形式

而只取其实部。将式（1-21）和式（1-22）代入式（1-36b）便得到自由粒子的平面波

如果粒子在三维空间运动，则上式可推广为

r是原点到波面任何一点的径矢。

玻恩对波函数的统计解释：波函数（或波函数振幅）的平方表示在单位体积中发现一个粒子的概率，称为概率密度。波函数是复数，而概率却必须是实正数，所以波函数的平方，应等于波函数ψ与其共轭复数ψ*的乘积。波函数既然具有这样的物理意义，必须满足一些条件。它必须是连续的、单值的、有限的，概率不会在某处发生突变，所以函数必须随处连续。在任何处，只能有一个概率，所以函数在任何处是单值的。概率不能无限大，所以函数值必须有限。不符合这三个条件的波函数是没有物理意义的，它不代表物理实在。另外，由于粒子必定要在空间中的某一点出现，所以粒子在空间各点出现的概率总和等于1，也就是

式中，V为空间体积。式（1-39）称为归一化条件，其积分应遍及整个空间。

2.定态薛定谔方程

一个微观粒子的状态可用波函数ψ（r，t）来描述，当ψ（r，t）确定以后，在空间某处发现一个粒子的概率以及任何力学量的测量值概率都完全确定了。因此，量子力学中最核心的问题就是要找出各种具体情况下描述系统状态的各种可能的波函数。这个问题由薛定谔提出的波动方程得以圆满解决。薛定谔方程是量子力学的基本方程，它不能由其他原理推导出来，它的正确性只能靠实验来检验。

下面是建立定态薛定谔方程的主要思路（并不是方程的理论推导）。(www.xing528.com)

一个具有能量E和动量p的自由粒子波函数由式（1-38）给出，它可以写为

式中，

ψ（r）称为振幅函数，它是波函数中只与坐标有关，而与时间无关的部分，也称为波函数。振幅函数分别对x、y、z求二阶导数，将求得导数的三式相加，即有

其中∇²为拉普拉斯算符，定义为

如果粒子不是自由粒子而是在势场中运动，上述方程仍然成立。粒子的总能量E应是势能U和动能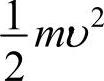之和，那么有p²=2m（E-U），将其代入（1-42）得

ψ只是坐标的函数，式（1-44）不含时间，这就是定态薛定谔方程。

3.薛定谔方程的意义

薛定谔方程是量子力学的基本方程，它揭示了微观物理世界物质运动的基本规律。它是原子物理学中处理一切问题的有力工具，在原子、分子、固体物理、核物理、化学等领域被广泛应用。

薛定谔认为，玻尔等人的量子论都是假设的，认为玻尔的这些“量子条件具有完全奇怪的和不可理解的性质”。应该取代为在满足波函数单值、有限、连续的条件下以及一定的边界条件下求解波动方程的本征值，从而求得一组分立的本征率。“整数性质是这一方法的自然结果”，而不是人为规定。薛定谔方程的解确实具有整数性，它真正地将量子论带到科学的领域。

狄拉克把狭义相对论引入到量子力学中，这就成为相对论的量子力学的基础。他还运用众所周知的狄拉克符号法这种独特的表述方法，发展了称为变换理论的一般的量子理论，由此，量子论的体系可以说基本完成。