测量与测不准原理详解

1.宏观物体的测量和微观物体的测量

当研究物体的运动时，最初必须建立观测运动的手段。也就是说，应该跟踪它的轨道。使用可见光或电磁波跟踪宏观物体运动的理由，除了用这种方法传递信息非常快的优点之外，还由于光照射到物体上而物体的运动几乎没有改变的缘故。可见光的光子动量为10^-27kg·m·s^-1数量级，这样大小的动量与宏观物体运动时的动量（如1g的物体具有10m·s^-1速度时的动量为10^-2kg·m·s^-1）相比要小的多，所以光触及在物体上而产生的影响是完全可以忽视的。然而，当物体的质量非常小而其动量和光的动量具有相同大小时，物体的运动状态则由于光的触及发生变化。但是如果光没有触及到物体，就不可能知道它的位置，当然，也得不到关于运动状态的数据。

为了使物体受到的影响小，是否可用动量小而波长长的电磁波呢？可是在这种情况下，虽然动量变小，但由于波长长而给确定物体的位置带来不准确性。图1-12a、b分别表示用短波和长波测量物体时的情况。但是在后者的情况下，由于波的衍射效应，物体不能阻止波的传播，因此，不能起到测量位置的作用。

实际上，要这样研究物体的运动时，必须要考虑观测问题。可是在牛顿力学中，认为这个问题是与运动定律无关系的次要问题。确实在研究一般物体运动时，观测只是手段。当进行观测的时候，对运动状态本身不会有任何影响。将这种观点无限制地推广，为了观测，所进行的操作对物体运动状态产生很大影响时，就会认为牛顿力学仍旧适用的看法是有问题的。

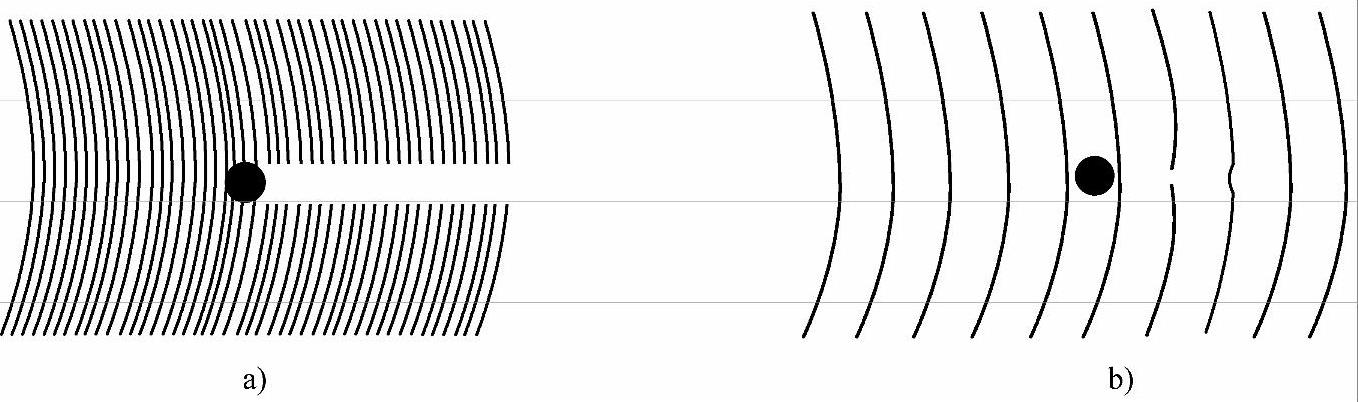
图1-12 物体对波的影响

a）短波情况 b）长波情况

运动状态不受影响而能跟踪电子的位置是不可能的。像阴极射线管（示波器），电子束碰撞在荧光膜上而发出荧光，由于能发光的荧光屏可以表示自身的位置，所以通过管内的电子在这一瞬间，电子的动量与碰撞前是完全不同的。再有关于荧光屏上的电子位置，严密地来说，小于荧光光点大小的是不能正确指示的。又因为电子束是由许多电子组成的。究竟是哪个电子在什么时候碰撞在荧光屏上，要正确地获得这些数据是格外困难的。

2.测不准原理

测不准关系是海森伯在1927年根据对一些理想实验的分析和德布罗意关系而得出的。即微观粒子在位置与动量两者不确定量之间的关系满足

最初，海森伯用波包概念第一次定量地导出了粒子坐标和动量之间的不确定关系。当玻尔看到论文的初稿时，认为波粒二象性应当成为量子理论解释的出发点，并且果然通过波粒二象性的论证，重新导出了不确定关系。玻尔说，一个在空间和时间上都是有限的实际波场，只能由原则上与无限多的频率ν值和波矢k值相对应的基本波叠加而成。他从经典波动概念出发，把物质粒子的波动性看成是三维空间中连续分布的波包（图1-13），对于一个位置确定的波包，必须满足ΔxΔλ≥λ²。即要无限精确地测准波长（Δλ→0），就必须在无限扩展的空间中进行观测（Δx→∞）。再运用德布罗意关系λ=h/p得到Δλ=（h/p_x²）Δp_x。代入ΔxΔλ≥λ²式，便有

ΔxΔp_x≥h （1-28a）

这就是粒子位置和动量的不确定关系式。

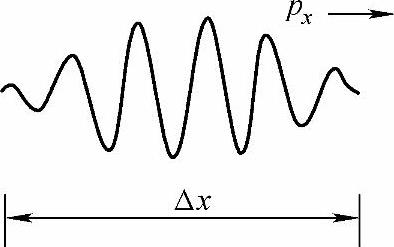
图1-13 波包

海森伯提出不确定关系时，量子力学的基本数学结构和物理解释都已建立起来。1927年海森伯的文章刚发表出来，Kennard就运用量子力学的数学公式推导出不确定关系

式中，ΔE表示能量的不确定量；Δt表示时间的不确定量。

下面利用波长很短的γ射线显微镜的设想实验对这个问题作详细的讨论。图1-14所示的是用γ射线确定电子位置的装置。入射的γ射线的光子和电子碰撞，并通过透镜应该到达检测器。因为γ射线能通过OAP，也应该通过OBP，所以，∠AOB为2α时，光子动量的x分量具有和的宽度。设它为Δp_x就成为

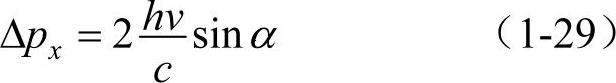
另一方面，根据物理光学，显微镜的分辨率或者x位置的不确定性，由下式给出(www.xing528.com)

由式（1-29）和式（1-30）得如下关系

ΔxΔp_x≈h （1-31）

在实际上，因为不确定性更大，所以可写为

ΔxΔp_x≥h （1-32）

图1-14 γ射线显微镜（设想实验）

在图1-14中，用γ射线捕获电子时，假设只有Δx的不确定性，这意味着在γ射线捕获的时间t内，只有如下的不确定性

式中，ν_x是γ射线碰撞前电子速度的x分量。另一方面，因为电子的能量为，所以当p_x只有Δp_x的变化时，则E的变化为

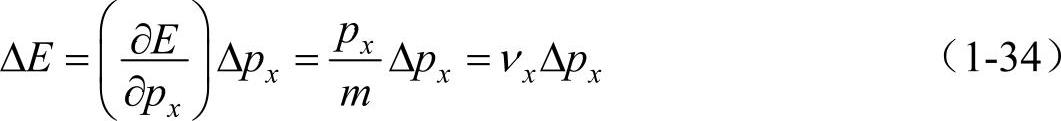
由式（1-32）、式（1-33）和式（1-34）得下列关系

也就是说，电子的能量和在它观测所需要的时间t内，可以有不确定性或是互补的关系。

3.测不准关系的物理解释

在不确定关系提出之后，物理学家对它的物理本质具有不同理解，对它是由什么因素引起以及它的意义是如何具有不同评述。

海森伯和波尔等人提出了一种“扰动说”。认为不确定关系来源于在单次测量中宏观仪器对被测量的微观系统的不可控制和不可预计的扰动。在海森伯最早关于γ射线显微镜的论证里，他认为由于“光子被电子散射的瞬间，电子的动量产生一个不连续的改变”，“因此，电子的位置测定得愈精确，动量就知道得愈不精确，反之亦然”。玻尔也讲过：“按照量子理论，正是由于不可能忽略系统和测量器械的相互作用，就意味着每一次观察都将引入一个新的不可控制的要素。”

另一种看法认为不确定关系是波粒二象性的反映。玻尔就是根据粒子的波粒二象性来说明不确定关系的。其方法是假定电子完全可用波概念来表示，那么粒子概念可应用性就受到限制，这个限制就由海森伯关系表达出来。换句话说，假定波理论的最简单的概念是对的，这些波概念就可取来作为评判粒子图景的基础，从而显示出粒子图景仅在一定限度上可用。例如，如果一个粒子出现的地点已被确切地确定了，则用波图景就必须说：在这里存在着一个缩拢到一个很小空间上的“波包”。可是这样一个波包是不稳定的，它立刻分裂散开。但是用粒子图景，这就意味着对这粒子此后运动的速度不能赋予任何确定的数值和方向。在这里应用粒子速度概念在一定程度上是不确定的，事实上粒子位置知道得越准，粒子速度就越不确定。

在玻恩提出波函数的统计解释以及用量子力学的基本原理导出不确定关系后，物理学家提出对不确定关系的统计解释。即不确定关系的不确定量都应当指的是多次测量里观测值偏离其平均值的统计散布，不确定关系就是两种统计散布（即涨落）的乘积所受到的限制。

现在的物理教科书一般都主张不确定关系是微观粒子波粒二象性的宏观表现，认为粒子的波动性使得粒子在任何一时刻不具有确定的位置，也不具有确定的动量。

不确定关系说明了用经典力学描述微观粒子运动时所存在的局限性，给人们指出了使用经典粒子运动概念的一个限度。不确定关系划分了经典力学和量子力学的界限。