德布罗意物质波的特性与应用

以玻尔理论为基础的量子理论（称之为旧量子论），尽管取得了不少令人惊奇的成果，但也存在着严重的缺陷与不足，遇到了越来越多的困难。1923年，德布罗意提出“物质具有波粒二象性”的假设，创造性地做出“电子具有波动性”的预言，为量子论的发展开辟了一条崭新的途径，打通了薛定谔通往波动力学的道路。1926年，玻恩提出波函数的统计解释，找到了波与粒子统一的线索，把波与粒子统一到概率波概念的基础上，为量子力学提供了全新的概念基础。1927年，海森伯提出了不确定性关系（或原理），加深了人们对量子本质的认识，极大地推进了人类认识微观客体本质属性的历史进程。

1.德布罗意物质波假设

在汤姆孙通过研究阴极射线确定射线的荷质比并确定电子的存在时，人们认识到电子的微粒特性。至于电子的波动性则是在发现电子27年后由年仅25岁的德布罗意大胆假设实物微粒也应像光子一样具有波粒二象性之后提出的。德布罗意后来谈到他如何把光的波粒二象性推广到实物粒子上来的。他在1964年致库伯利（Kubli）的信中写道：在1922～1923年期间，当我开始获得波动力学的基本想法时，我的意图是把爱因斯坦发现的光的波粒共存现象推广到所有粒子，因此，我开始把爱因斯坦建立的光量子公式ε=hν和p=hν/c=h/λ，应用到光子以外的其他粒子上。

德布罗意认为，质量为m的粒子、以速度ν匀速运动时，具有能量E和动量p；从波动性方面来看，它具有波长λ和频率ν，而这些量之间的关系也和光波的波长、频率与光子的能量、动量之间的关系一样，应遵从下述公式

E=mc²=hv （1-21）

所以对具有静止质量m₀的实物粒子来说，若粒子以速度ν运动，则和该粒子相联系的平面单色波的波长λ是

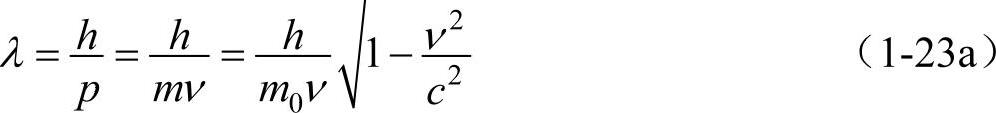
式（1-23）称为德布罗意公式。人们常把这种和物质相联系的波通常称为德布罗意波。薛定谔在诠释波函数的物理意义时，把这种波称为物质波。如果ν《c，那么

德布罗意把他的相波概念应用到以闭合轨道绕核运动的电子，从而推出了玻尔的量子化条件，这是德布罗意波能够成立的一个有力证据。德布罗意提出“只有满足相波谐振的那条轨道才是稳定的轨道。”电子的轨道是由对闭合路径的积分取整数值来确定，即

谐振的条件是l=nλ，即电子轨道的周长是相波波长的整数倍，亦即

这正是玻尔假设中有关电子轨道角动量量子化的条件。这就是说，氢原子中作稳定的圆周运动的电子相应的波必须是一个驻波，其形状如图1-9所示。即电子绕核一周后，驻波应光滑地衔接起来。

2.物质波的实验验证

最早从实验上证实电子衍射现象的是美国的戴维孙（C.J.Davisson）和他的合作者革末（L.H.Germer）。1926年他们将电子枪射出的电子束投射到镍单晶体表面上，研究了散射电流与轰击电压和散射角的关系，肯定了这是电子衍射的结果。经过定量计算，证明了德布罗意波长公式的正确性。

图1-9 电子的德布罗意波(www.xing528.com)

图1-10是戴维孙和革末的电子在晶体上衍射的实验装置示意图。从加热灯丝K出来的电子，经电势差U加速后，通过一组阑缝D，成为很细的平行电子射线，以一定的角度投射到镍单晶体M上，经晶面反射后用集电器B收集。进入集电器的电子流强度I可用与B相连的电流计G来量度。实验时，使图中所示的两个φ角相等，并保持不变；改变电势差U，量度相应的电子流强度I。实验结果如图1-11所示，在电势差U单调地增大时，电子流强度I不是单调地增大，只有当电势差为某些特定值时，电子流才有极大值。

图1-10 电子在晶体上衍射实验装置示意图

图1-11电子流强度与电势差的关系

为了解释这一实验结果，用X射线衍射的结果来分析。X射线在晶体上反射时，只有入射线的波长λ符合布拉格公式2dsinφ=kλ）k=0，1，2，…；d为晶面间距）的那些射线才能在一定的角度φ观察到反射线。如果承认电子也有波的性质，并把上述实验结果看做是电子波的衍射。那么，在d和φ给定时，仅当电子波波长λ满足布拉格公式时，才能按反射定律自晶面反射。由德布罗意波公式和布拉格公式得

即电势差U满足式（1-26）时，电子流强度I为最大值。由此计算所得的电势差U的各个量值和实验结果相符合，从而证明了德布罗意物质波假设是正确的。

1927年，汤姆孙（G.P.Thomson）和里德做了高能电子束透射金属薄层的实验，观察到了衍射环。根据这些圆环的半径计算出电子波的波长，证明了德布罗意公式，证实了电子的波粒二象性。1960年约恩孙（C.Jonson）直接做了电子双缝干涉实验，从屏上得到了类似光的杨氏双缝干涉图样。电子的波动性获得了实验证实以后，在其他的一些实验中也观察到中性粒子，如原子、分子和中子等微观粒子，也具有波动性，同样证实德布罗意公式的正确性。由此可见，一切微观粒子都具有波动性，德布罗意波的存在已是确实无疑的了。德布罗意公式已成为揭示微观粒子的波—粒二象性的统一性的基本公式。

3.物质波是概率波

（1）玻恩的统计解释

1926年，波恩提出了德布罗意波的统计意义，认为波函数体现了发现粒子的概率，这是每个粒子在它所处环境中所具有的性质。如果有大量的粒子，那么在某处粒子的密度就与此处发现一个粒子的概率成正比。把这情况同光来对比，光的强弱同光子的数目成正比，而在某处的光子数同该处发现一个光子的概率成正比，但我们知道光的强弱是同光波的电场或磁场强度的平方成正比的，即与光波的波函数的平方成正比，足见在某处发现一个光子的概率同光波的电场或磁场强度的平方（即波函数的平方）成正比。这样来类比，可见在某处发现一个实物粒子的概率同德布罗意波的波函数平方ψ²成正比。可以把体积dτ中发现一个粒子的概率表达为dω=ψ²dτ。由此，ψ²代表在单位体积内发现一个粒子的概率，因而称概率密度。这就是德布罗意波函数的物理意义。

玻恩提出的波函数ψ与经典的波函数有类似之处，但是它们的意义是完全不同的。经典的波函数意味着有某种实在的物理量的空间分布作周期性的变化，是可以测量的，而概率波ψ在一般情况下是不可测量的。一般可以测量的只是ψ²，它的含义是概率。对于概率分布来说，重要的是相对概率分布。显而易见，ψ（r）与Cψ（r）（C为常数）所描述的相对概率分布是完全相同的；而经典波的波幅若增加一倍，则相应的波动能量将为原来的4倍，代表完全不同的波动状态。

（2）概率波对电子双缝干涉实验的解释

怎样解释电子双缝干涉实验？是否可以用波的干涉理论来说明？电子运动的波列到达双缝（双缝假设为A和B）后，将在双缝A和B处形成两个子波，两个波叠加后在接收屏上得到双缝干涉图样。但是这样的描述与电子粒子性相矛盾。到目前为止，我们知道电子是不可分割的，一个电子通过A和B时被分成两部分，彼此进行干涉是不可能的。反之，如果认为电子到达双缝时只有一条狭缝起作用，即每个电子仅仅从其中一条通过，则这种观点虽然维护了电子的粒子性，却又与实验事实明显不符。应该说，电子通过缝A时，缝B是否打开对它不应有任何影响。同样，电子通过缝B时，缝A的存在也应与它毫无关系。按照这种观点必然得到如下结论：先打开缝A关上缝B，然后再打开缝B关上缝A，应得到与同时打开双缝相同的衍射图样。但事实却不是如此，先后依次打开一条缝得到的必然是两个单缝衍射图样的叠加，屏上电子的强度应是分别打开时强度之和，不可能得到双缝干涉图样。这就是说，尽管粒子性要求每个电子只可能从一条缝通过，但双缝仍然同时在起作用，与只打开单缝电子的“感受”是不同的。

概率波的概念既能维护电子的粒子性，又能体现电子的波动性。由于概率波给出的是电子出现的概率，所以不要求分割电子。而电子的概率分布又是由波函数决定的，所以能给出干涉、衍射图样，又体现了波动性。电子通过双缝时，同时打开两个缝与分别先后各打开一个缝对于电子来说是有区别的，在前一情形每个电子都有两种机会，即可以从A或B通过，而在后一情形就只存在一种机会。因此，应当分别用两种不同的概率波来表示这种情况，即波函数ψ应是两种不同的数学表达式，分别给出不同的干涉图形，即分别是双缝或单缝衍射图样。一个表示有机会通过A和B两个缝的概率波并不破坏电子的粒子性，它是说明每个电子有机会通过缝A也有机会通过缝B，而没有要求一个电子分成两半，分别通过A和B。

电子到达接收屏后也不会发生矛盾，这时经过衍射的概率波将给出电子在屏上分布的概率，例如亮条纹处概率大，暗条纹处概率小等。电子到达屏时实际上只落在一个点上，不过落在哪个点上是按概率波给出的概率分布的。在大量电子参加双缝实验时，各个电子都以同样的概率波表示，大量电子到达接收屏后必然在概率大的地方电子多（出现亮条纹），在概率小的地方少（出现暗条纹）。因此，用概率波描述电子能很好地将电子的波动性和粒子性结合起来。