电机变频调速：恒转矩的优势及应用

1.电压随频率调节的规律

由公式n1=可知，当电机极对数不变时，电动机的同步转速和电源频率成正比，若连续改变电源频率就可以连续改变同步转速，从而连续平滑地改变电动机的转速。但是单一调节电源的频率，将导致电动机运行性能恶化，其原因可分析如下：

三相异步电动机正常运行时，定子漏阻抗压降很小，所以可以认为，定子每相电压U1≈E1，气隙磁通为

在变频调速时，如果只降低定子频率f1，而定子每相电压不变，则Φ0要增大。由于在正常（额定）情况时电动机的主磁路就已经接近饱和，若频率下降，Φ0增大，主磁路必然过饱和，这将使励磁电流急剧增大，铁耗增加，功率因数下降。若频率增加，则Φ0减少，使电磁转矩和最大电磁转矩下降，过载能力降低，电动机的容量也得不到充分利用。

因此，为了使电动机保持较好的运行性能，要求在调节频率f1的同时，改变定子电压U1，以维持Φ0不变，或者保持电动机的过载能力不变。电压随频率按什么规律变化最为合适呢？一般认为，在任何类型的负载下变频调速时，若能保持电动机的过载能力不变，则电动机的运行性能较为理想。电动机的过载能力为

在最大转矩式（3-39）中，当f1较高时，（x1+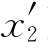）≫r1，故可略去r1，又因为（x1+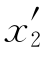）=2πf1（L1+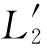），由此得到的最大转矩公式代入式（3-43）中可得

式中：常数为定转子绕组的漏电感。

为了保持变频前后λT不变，要求下式成立

即

式中加“′”的量表示变频后的量。

式（3-45）表示变频调速时，电压U1随频率f1变化的规律，此时电动机的过载能力将保持不变。

变频调速时，U1与f1的调节规律是和负载的性质有关的，通常分为恒转矩变频调速和恒功率变频调速两种情况。

（1）恒转矩变频调速。对于恒转矩负载，TN=T′N，于是式（3-45）可变为

说明，在恒转矩负载下，若能保持电压与频率成正比调节，则电动机在调速过程中既能保证电动机的过载能力λT不变，又能保证主磁通Φ0不变。这也说明变频调速特别适合恒转矩负载。

（2）恒功率变频调速。对于恒功率负载，要求在变频调时电动机的输出功率保持不变，则(www.xing528.com)

因此

将式（3-48）代入式（3-47）中，得

即在恒功率负载下，如能保持=常数，则电动机的过载能力λT不变，但主磁通Φ0将发生变化。

2.变频调速时电动机的机械特性

变频调速时电动机的机械特性可用以下式（式中忽略了r1、r'2）来分析。

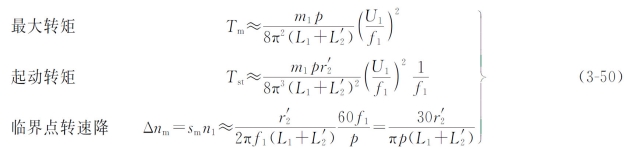
以电动机的额定频率f1N为基频。在生产实践中，变频调速时电压随频率的调节规律是以基频为分界线的，于是分以下两种情况：

（1）在基频以下调速时，可保持=常数，即恒转矩调速。由式（3-50）可知，当频率f1减少时，最大转矩Tm不变，起动转矩Tst增大，临界点转速降Δnm不变。因此，机械特性曲线随频率的降低而向下平移，如图3-29（a）中虚线所示。但实际上由于定子电阻r1的存在，随着频率f1的下降=常数），Tm将减小，当频率很低时，Tm将减小很多。如图3-29（a）中实线所示。为保证电动机在低速时有足够大的Tm值，U1应比f1降低的比例小一些，使U1/f1的值随f1的降低而增加，如图3-30中直线2，这样才能获得图3-29（a）中虚线所示的机械特性。

图3-29　变频调速机械特性曲线

（a）U1/f1=常数时变频调速的机械特性；（b）恒转矩和恒功率变频调速时的机械特性

（2）在基频以上调速时，频率从额定频率往上增加，但电压却不能增加得比额定电压还高，最高保持为额定电压不变。由式（3-42）可知，这样随着频率升高，磁通必然会减少，又由式（3-50）可知，此时，最大转矩和起动转矩都随着频率的增高而减少，但临界点转速降不变，即不同频率下各条机械特性曲线近似平行，如图3-29（b）所示。此时近似为恒功率调速，相当于直流电动机弱磁调速的情况。

图3-30　异步电动机变频调速控制特性

1—不带定子电压补偿；2—带定子电压补偿

把基频以下和基频以上两种情况结合起来，可以得到图3-30中所示的异步电动机变频调速控制特性，图中曲线1为不带定子电压补偿时的控制特性，曲线2为带电压补偿时的控制特性。如果电动机在不同转速下都具有额定电流，则电动机都能在温升允许条件下长期运行，这时转矩基本上随磁通变化而变化，即在基频以下属于恒转矩调速，而在基频以上属于恒功率调速。

变频调速的主要优点是调速范围大、调速平滑、机械特性较硬、效率高。高性能的异步电动机变频调速系统的调速性能可与直流调速系统相媲美。但它需要一套专用变频电源，调速系统较复杂、设备投资较高。近年来随着晶闸管技术的发展，为获得变频电源提供了新的途径。晶闸管变频调速器的应用大大促进了变频调速的发展。变频调速是近代交流调速发展的主要方向之一。