1.整距集中绕组的基波磁动势
设有一台两级交流电机,气隙是均匀的。其中一个整距绕组U1-U2通过正弦交流电流ic,假设某一瞬间电流的方向由U1流入,从U2流出,则线圈磁动势在某瞬间的分布如图2-25(a)中虚线所示,它产生的是两极的磁场。对定子而言,上端为S极,下端为N极,为-2极磁场。若绕组的匝数为Nc,则根据全电流定律,每根磁感线所包围的全电流均为

将图2-25(a)展开为图2-25(b)。选定绕组U2、U1的轴线处为坐标原点,用纵坐标表示磁动势fc,横坐标x表示沿气隙圆周离开原点的空间距离。若略去铁芯中的磁阻不计,可认为绕组产生的磁动势全部降落在两个气隙上,并均匀分布,则定子内圆各处气隙中的磁动势正好等于绕组磁动势的一半,即![]() 。同时规定,磁力线从定子进入转子的磁动势为正,反之为负,则可得到沿气隙圆周空间分布的磁动势曲线,如图2-25(b)所示。可见,磁动势波形为矩形波,宽度等于线圈宽度,高度为
。同时规定,磁力线从定子进入转子的磁动势为正,反之为负,则可得到沿气隙圆周空间分布的磁动势曲线,如图2-25(b)所示。可见,磁动势波形为矩形波,宽度等于线圈宽度,高度为 。
。

图2-25 两极单相绕组的脉振磁场和磁动势
(a)单相绕组磁力线分布图;(b)气隙磁动势分布图
如果绕组中的电流为直流电,则矩形波的幅值不随时间发生变化。如果绕组中的电流为交流电,且其随时间按正弦规律变化,即ic= Icsinωt,则整距绕组磁动势为
Icsinωt,则整距绕组磁动势为
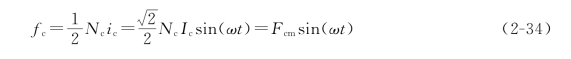
式中:![]() 为气隙磁动势的幅值。
为气隙磁动势的幅值。
式(2-34)表明,磁动势矩形波的幅值随时间按余弦规律变化,变化的频率即为交流电源的频率,但其轴线位置在空间保持固定不变。当电流达到正的最大值时,磁动势矩形波的幅值为正的最大值![]() ;电流为零时,磁动势矩形波的幅值也为零;当电流为负的最大值时,磁动势矩形波的幅值为负的最大值
;电流为零时,磁动势矩形波的幅值也为零;当电流为负的最大值时,磁动势矩形波的幅值为负的最大值![]() ,如图2-26所示。磁动势在任何瞬间,空间分布总是一个矩形波。通常把这种空间位置固定不动,而幅值和方向随时间而变的磁动势称为脉振磁动势。
,如图2-26所示。磁动势在任何瞬间,空间分布总是一个矩形波。通常把这种空间位置固定不动,而幅值和方向随时间而变的磁动势称为脉振磁动势。
对于空间按矩形波分布的脉振磁动势,可用傅里叶级数分解为基波和一系列奇次谐波,如图2-27所示。其展开式为

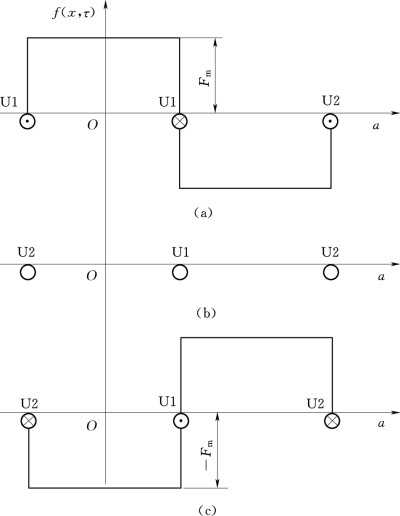
图2-26 不同时刻的脉振磁动势
(a)ωt=0,i=Im;(b)ωt=90°,i=0;(c)ωt=180°,i=-Im
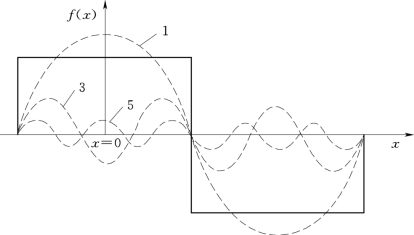
图2-27 矩形波磁动势的分解
式中:γ为谐波次数;![]() 为用电角度表示的空间距离;
为用电角度表示的空间距离;![]() 为基波磁动势的最大幅值;
为基波磁动势的最大幅值;![]() 为γ次谐波磁动势的最大幅值。
为γ次谐波磁动势的最大幅值。
式(2-35)中的第一项即为基波磁动势分量,可见整距绕组的基波磁动势在空间按余弦分布,其幅值位于绕组轴线,零值位于线圈边,空间每一点磁动势的大小均随时间按正弦规律变化,故整距绕组的磁动势的基波仍是脉振磁动势,其磁动势的幅值为Fcm1。
2.单相脉振磁动势
(1)整距分布绕组的磁动势。每个绕组都是由q个相同匝数的线圈串联而成,各线圈依次按定子圆周在空间错开一个槽距角α。因此,每个线圈所产生的基波磁动势幅值相同,而幅值在空间相差α电角度。又由于基波磁动势在空间按余弦规律变化,故它可用空间矢量表示,绕组的基波磁动势为q个线圈基波磁动势空间矢量和。
不难看出,整距分布绕组基波磁动势如同电动势计算一样,因此引入同一基波分布系数kq1,用来计及绕组分布对基波磁动势的影响,于是得到整距分布线圈组基波磁动势的最大幅值为
![]()
(2)一组双层短距分布绕组的基波磁动势。由于是短距绕组,所以同一相上、下层导体要移开一个距离,这个距离即是绕组节距所缩短的电角度(180°-γ)。
由于磁动势大小和波形只取决于槽内线圈组边的分布及电流的情况,而与各线圈组边的连接次序无关。因此可将上层线圈组边等效地看成是一个单层整距分布线圈组,下层线圈组边等效地看成是另一个单层整距分布线圈组,上下两线圈组在空间相差(180°-γ)电角度,因此双层短距分布绕组基波磁动势如同电动势一样,其大小为两个等效绕组基波磁动势的相量和,因此,又可引入短距系数来计及绕组短距的影响。于是双层分布绕组基波磁动势的最大幅值为

(3)相绕组的磁动势。因为每对极下的磁动势和磁阻构成一条分支磁路,若电机有p对极,就有p条并联的分支磁路,故一相绕组基波磁动势幅值,便是该相绕组在一对极下线圈所产生的基波磁动势幅值,并不是组成一相绕组所有线圈组的合成磁动势。由此可见相绕组基波磁动势幅值仍可用式(2-37)来计算。为了使用中更方便,一般用相电流Ip和每相串联匝数N来代替线圈中电流Ic和线圈匝数Nc,若绕组并联支路数为α,则式(2-37)改写为(https://www.xing528.com)

式中:Ip=αIc;N为每相串联匝数,参见式(2-24)和式(2-25)。
单相绕组的基波磁动势仍为在空间按余弦规律变化,幅值大小随时间按正弦规律变化的脉振磁动势。其表达式为
![]()
3.单相基波脉振磁动势的分解
根据三角公式![]() ),可将式(2-39)分解为
),可将式(2-39)分解为
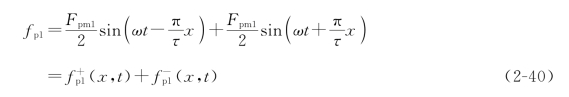
可见,一个脉振磁动势可分解成两个磁动势:f+p1(x,t)和f-p1(x,t)。下面具体分析这两个磁动势的性质。
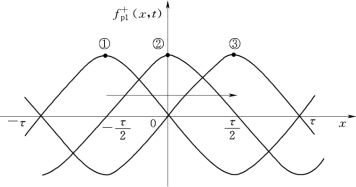
图2-28 正向旋转磁动势波
(1)![]() 的性质。下面取幅值
的性质。下面取幅值![]() 这一点来研究,幅值出现的条件是
这一点来研究,幅值出现的条件是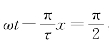 ,解得x
,解得x![]() ,即x=f(t),这说明幅值的空间位置x随时间t而变,下面取三个瞬时进行分析:①当ωt=0时,x=-
,即x=f(t),这说明幅值的空间位置x随时间t而变,下面取三个瞬时进行分析:①当ωt=0时,x=-![]() ;②当ωt=
;②当ωt=![]() 时,x=0;③当ωt=π时,x=
时,x=0;③当ωt=π时,x=![]() ,如图2-28所示。
,如图2-28所示。
综上分析可知:
1)随着时间的推移, (x,t)朝x轴正向移动,故
(x,t)朝x轴正向移动,故 (x,t)被称为正向旋转磁动势。
(x,t)被称为正向旋转磁动势。
2)正向旋转磁动势的幅值为单相脉振磁动势最大幅值的一半,即![]() 。
。
3)线速度为
![]()
因圆周长为2pτ,故旋转速度为
![]()
(2)![]() 的性质。同理也取三个瞬时进行分析:①当ωt=0时,x=
的性质。同理也取三个瞬时进行分析:①当ωt=0时,x=![]() ;②当ωt=
;②当ωt=![]() 时,x=0;③当ωt=π时,x=-
时,x=0;③当ωt=π时,x=-![]() 。由分析可知,它也是一个幅值恒为
。由分析可知,它也是一个幅值恒为![]() 的旋转磁场,其转速也为n1=
的旋转磁场,其转速也为n1=![]() ,所不同的是其转向与
,所不同的是其转向与![]() 相反。如图2-29所示。
相反。如图2-29所示。

图2-29 反向旋转磁动势波
综上分析可得如下结论:
1)单相绕组的基波磁动势为一正弦脉振磁动势,它可分解为大小相等、转速相同而转向相反的两个旋转磁动势。
2)反之,满足上述性质的两个旋转磁动势的合成即为脉振磁动势,如图2-30所示,图中产生脉振磁动势的电流表达式为i=Imsinωt,图2-30(a)中表示ωt=![]() 时刻,图2-30(b)中表示ωt=
时刻,图2-30(b)中表示ωt=![]() 时刻,图2-30(c)表示ωt=
时刻,图2-30(c)表示ωt=![]() 时刻,而图2-30(d)表示ωt=π时刻的情形。
时刻,而图2-30(d)表示ωt=π时刻的情形。

图2-30 基波脉振磁动势分解为两个旋转磁动势
3)在图2-30中,用空间矢量 和
和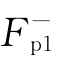 分别表示了正、反向旋转磁动势,由于
分别表示了正、反向旋转磁动势,由于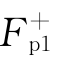 和
和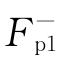 在旋转过程中,其大小不变,两矢量顶点所描绘的轨迹均为一圆形,故又称这两个磁动势为圆形旋转磁动势。
在旋转过程中,其大小不变,两矢量顶点所描绘的轨迹均为一圆形,故又称这两个磁动势为圆形旋转磁动势。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




