非正弦分布磁场下绕组产生的高次谐波电动势

在实际的电机运行中，气隙磁通密度分布曲线并不是理想的正弦波形，利用傅里叶级数可以将非正弦磁场分解成为基波和一系列高次谐波，主磁极磁通密度的空间分布曲线如图2-24所示。图中还分别画出三次和五次谐波所对应的转子模型。

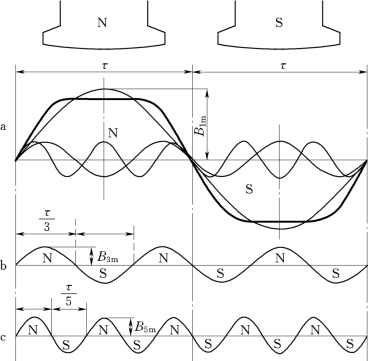
图2-24　主磁极磁通密度的空间分布

因此发电机的感应电动势除基波外，还存在一系列高次谐波。产生的原因有两方面，一方面是发电机气隙磁通密度沿气隙空间分布的波形不是理想的正弦波；另一方面是由于电枢铁芯和转子铁芯有齿、槽造成气隙磁阻不均匀。这里主要讨论非正弦分布磁场产生的高次谐波电动势。

谐波电动势的计算方法和基波电动势的计算方法相似。由图2-24可知，v次谐波磁场的极对数为基波的v倍，而极距则为基波的，即

v次谐波极对数为

v次谐波极距为

由于谐波磁场也因转子旋转而旋转，其转速与基波相同，均为转子转速，即nv=n1，因Pv=vP，故在定子绕组内感生的高次谐波电动势的频率为(www.xing528.com)

式中：f1为基波电动势的频率，。

根据式（2-26）可知，v次谐波相电动势的有效值为

式中：Φv为v次谐波的每极磁通量；kwv为v次谐波的绕组系数。

式中：kyv和kqv为v次谐波的短距系数与分布系数。

假如对基波而言，短距对应角和槽距电角分别为γ和α电角度。对v次谐波而言，由于极对数是基波的v倍。所以短距对应角和槽距电角分别为vγ和vα电角度，由此可得

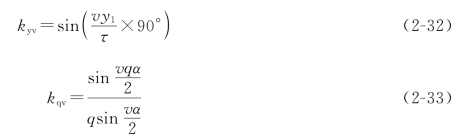
高次谐波电动势对相电动势大小影响很小，它主要影响的是电动势的波形，会使电动势波形变坏，产生许多不利的影响。如发电机的附加损耗增加、效率下降、温升升高，还可能引起输电线路谐振而产生过电压，对邻近输电线的通信线路产生干扰，使异步电动机的运行性能变坏。因此为了改善电势的波形，必须尽可能地削弱电动势中的高次谐波，特别是影响较大的三次、五次、七次谐波。