空载情况下的等效电路和相量图

1.相量图

在变压器中，既有电路问题又有磁路问题，如果能将变压器中的电和磁之间的相互关系，用一个电路的形式来表示，将使分析计算大为简化。这种表示变压器在正常运行时的电磁关系称为等效电路。

由前面的分析可知

从电路的观点来看，其中漏感电动势可以看作是电流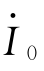流过漏电抗xσ1所引起的电压降。现用同样的方法来处理由主磁通所引起的感应电动势，考虑到主磁通在铁芯中引起的铁损耗，故不能单纯地引入一个电抗，还应引入一个电阻，即用一个阻抗Zm把和电流联系起来，其表达式为

式中：Zm=rm+jxm为变压器的励磁阻抗；rm为变压器的励磁电阻，对应于铁耗的等效电阻；xm为变压器的励磁电抗。

必须明确的是，rm既不是绕组电阻，也不是铁芯电阻，它仅仅是一个用来模拟铁芯损耗的等效电阻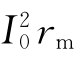，恰好等于铁损耗。

将式（1-25）代入式（1-16）中，于是变压器一次侧的电动势平衡方程式可写成

(www.xing528.com)

相应的等效电路如图1-20所示。

由变压器等效电路可知，变压器空载运行时，可看成是两个电抗器串联而成的电路，其中一个没有铁芯，其阻抗为一次绕组的漏阻抗r1和x1σ，r1是一次绕组的电阻，x1σ反映一次绕组漏磁通的作用；另一个有铁芯，其由励磁阻抗rm和xm组成，rm反映铁芯中的铁耗，xm反映主磁通的作用。从前面的分析可知，r1和x1σ为常数，而rm和xm不是常数，其与铁芯的饱和程度有关。当外加电压U1增大时，主磁通和感应电动势都将成比例增大，磁路将饱和，空载电流必须大大增加。因此，rm和xm将随着磁路饱和程度的增加而减小。但是，在实际变压器中，由于外加电压U1在额定值左右变化不大，故在定量计算时，可认为Zm基本不变。

在数值上，rm≥r1、xm≥x1σ，所以有时把r1、x1σ忽略不计，这样变压器空载时的等效电路就成为只有Zm的电路。所以在一定的外施电压下，空载电流的大小由励磁阻抗决定。从运行角度希望空载电流越小越好，故采用高导磁性能钢片的目的就是为了增大Zm，减少I0，以提高变压器的效率和功率因数。

2.相量图

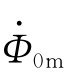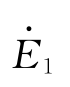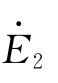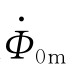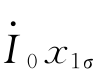根据变压器空载时的电磁关系式（1-16）和式（1-19），变压器空载运行时的相量图如图1-20所示。作图具体步骤如下：以主磁通为参考量，令其初相角为零；根据式（1-11）、式（1-12）可知，和滞后主磁通90°；由上面的分析可知，空载电流超前主磁通一个铁损角α，并且空载电流在一次绕组电阻上的电压降与同相位，在一次绕组漏电抗上的电压降超前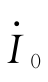90°。然后根据变压器空载时的一、二次电压平衡方程式，便可画出和。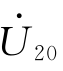

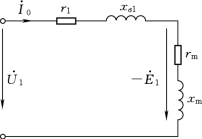
图1-20　变压器空载时的等效电路

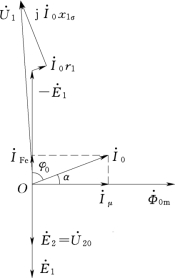
图1-21　变压器空载时的相量图

从变压器的空载相量图1-21可知，在横轴上的分量为磁化电流，在纵轴上的分量为铁耗电流。与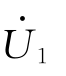之间的夹角φ0称为变压器空载运行时的功率因数角。由于φ0≈90°，因此，变压器空载运行时的功率因数cosφ0很低，一般在0.1～0.2之间。