变压器空载状态下的感应电动势

1.主磁通感应的感应电动势

若主磁通按正弦规律变化，即按照图1-16中参考方向的规定，则绕组感应电动势的瞬时值为

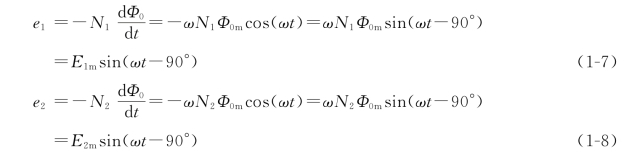
由上式可知，当主磁通Φ0按正弦规律变化时，一、二次绕组中的感应电动势也按正弦规律变化，但在相位上滞后于主磁通Φ090°，且感应电动势的有效值为

同理

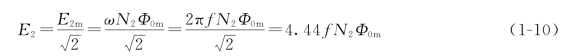
故电动势与主磁通的相量关系为

从上面的表达式中可以看出，当主磁通按正弦规律变化时，一、二次绕组中的感应电动势也按正弦规律变化，其大小与电源频率、绕组匝数及主磁通最大值成正比，且在相位上滞后于主磁通90°。

2.漏磁通感应的感应电动势

漏磁通感应的电动势的有效值相量表示为

式中：为一次侧漏磁通最大值。

为了简化分析计算，通常根据电工基础知识把上式由电磁表达式转化为习惯的电路表达形式，即

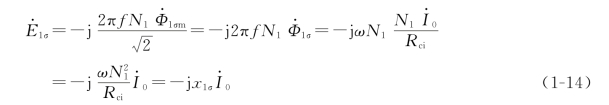
式中：x1σ为一次绕组漏电抗，反映漏磁通Φ1σ对一次侧电路的电磁效应；Rci为一次侧漏磁通所经过的闭合路径的磁阻。

由于漏磁通的路径绝大部分是非铁磁性物质，磁路不会饱和，是线性磁路，因此对已制成的变压器而言，Rci为常数，当频率f一定时，漏电抗x1σ也是常数，基本不随电源电压的改变而改变。

3.一、二次绕组电动势平衡方程式(www.xing528.com)

对于图1-16中规定的参考方向，根据基尔霍夫第二定律，一次侧电动势平衡方程式为

将式（1-14）中物理量代入式（1-15）可得

式中：r1为一次侧绕组的电阻；Z1=r1+jx1σ为一次侧绕组的漏阻抗。

空载时，一次侧的漏阻抗压降很小，若忽略漏阻抗压降，则

由式（1-17）可得，U1≈E1=4.44fN1Φm。因此，影响主磁通大小的因素是电源电压U1、电源频率f和一次绕组匝数N1。当电源频率f和一次绕组匝数N1一定时，主磁通的大小取决于电源电压U1的大小。

变压器空载时，二次绕组中只有主磁通产生的感应电动势e2与其端电压u20相平衡，则二次侧电动势平衡方程式为

用相量形式表示为

4.变压器的变比

在变压器中，一次绕组感应电动势与二次绕组感应电动势之比，称为变压器的变比，用k表示。即有

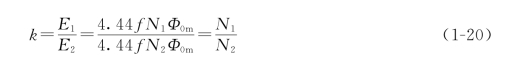
上式表明，变压器的变比等于一、二次绕组的匝数之比。

当变压器空载运行时，一、二次绕组端电压之比为

由上式可见，变压器空载运行时，变压器一次绕组与二次绕组的相电压之比就等于一、二次绕组的匝数比。因此，只要改变一次和二次绕组的匝数，就可得到不同的电压，这就是变压器能够“变压”的原理。因此，当k＞1时，称为降压变压器；k＜1时，称为升压变压器。