现在需要生成一个模拟切割导尿管时的作用力与反作用力。假定导尿管的直径为ϕ3mm,如图12-15所示。
基于物理条件,必须分几步来定义力。在生成表达式之前,应该先使用文字来描述这个运动:
步骤1:当刀片刚开始移动时没有作用力,此时为空行程。
步骤2:一旦刀片接触到导尿管,便会产生阻力,因为在导尿管被真正切割前会被压缩。
步骤3:导尿管被切断,力迅速降低。
步骤4:导尿管被切断,刀片继续在没有阻力的情况下前行。
步骤5:刀片在没有阻力的情况下回到开始位置。
上面提到的步骤1、4、5很简单,因为力的数值为零,真正的问题在于定义步骤2和步骤3的力。
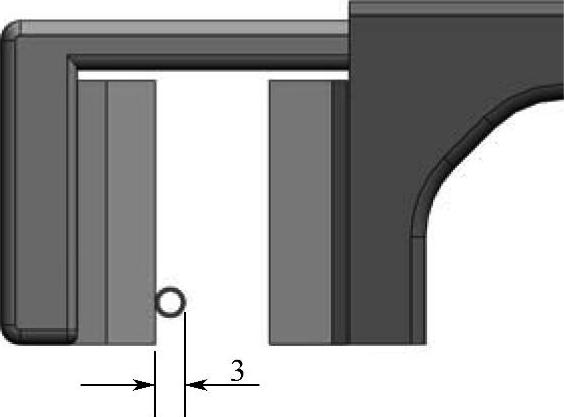
图12-15 指定尺寸
1.切割导尿管的力 在前面已经给出了实验数据,如图12-3和图12-4所示。
关键步骤
接下来将逐步创建完整的表达式,以查看其构造。
● 当刀片切割导尿管时会生成一个切割刀片位置的变量(图12-4中的变量x)。
● 图解显示第一段的力函数。
● 图解显示第一段和第二段的力函数。
● 图解显示第一段、第二段和第三段的力函数。
● 当切割刀片完全切断导尿管时(x=3mm)终止力函数。
● 当切割刀片在反方向移动时,在切割过程的这个第二部分设置力函数为零。
步骤13 确定刀片间隙
测量刀片之间的距离大小为7.25mm,如果导尿管的尺寸为ϕ3mm,则一开始就存在4.25mm的间隙。
步骤14 生成刀片之间位移的图解
按图12-16所示的顺序选择两条边线。如果用户按照相反的顺序选择,则图解也将是相反的。因为力是刀片位置的函数,所以需要知道刀片的位置。通过生成图解,得到了一个用于表达式的变量,如图12-17所示。
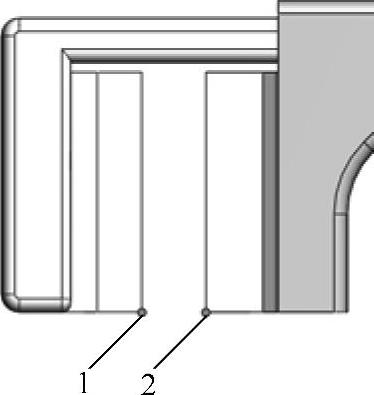
图12-16 选择边线
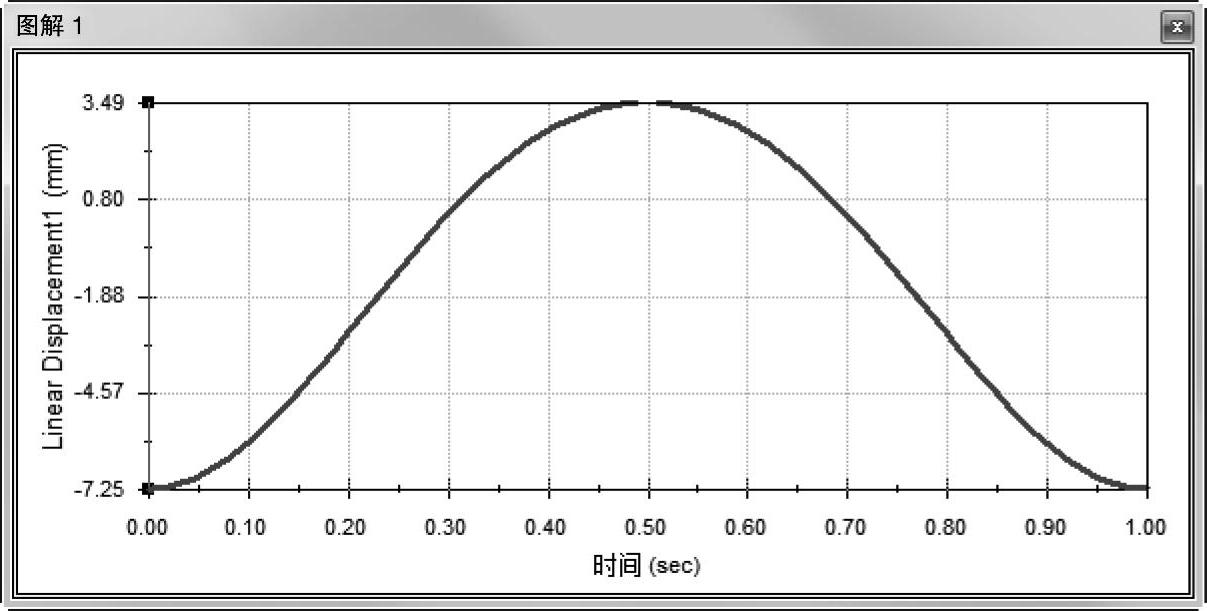
图12-17 查看图解(一)
注意(https://www.xing528.com)
这是第一个线性位移图解,因此取名为“Linear Displacement1”。同样地,将添加的力将取名为“Force1”,之后生成的线性速度图解将取名为“Linear Ve-locity1”。如果用户已经创建了其他图解或力,而且在这些步骤中得到的图解名称是不同的,则用户必须重命名这些图解,或替换为合适的名称。
2.生成力的表达式 下面这个部分的目标是在两个刀片之间生成作用与反作用力,以表现切割导尿管时所需的力,如图12-18所示。
在生成力的表达式时不会直接加载作用力到刀片上,而是将使用虚构的力,并保证不会影响到运动分析的输出。接着将应用这个力到fixed_cutter。因为SolidWorksMotion是一个刚体分析工具,任何作用在固定零件上的力都不会对运动分析产生影响。
图12-18 生成力
步骤15 添加一个力
这个力不会影响到结果,因为它作用在一个不动的零件上。将使用它来构建作用力或反作用力的完整表达式,如图12-19所示。
将这个力定义为一个函数,等效于在前面图解中定义的Displace-ment1,如图12-20所示。
步骤16 运行仿真
运行该仿真1s。
图12-19 添加力
步骤17 生成一个图解
图解显示【反作用力】的【Y分量】,如图12-21所示。现在这个力和活动刀片的位置便直接关联起来了。
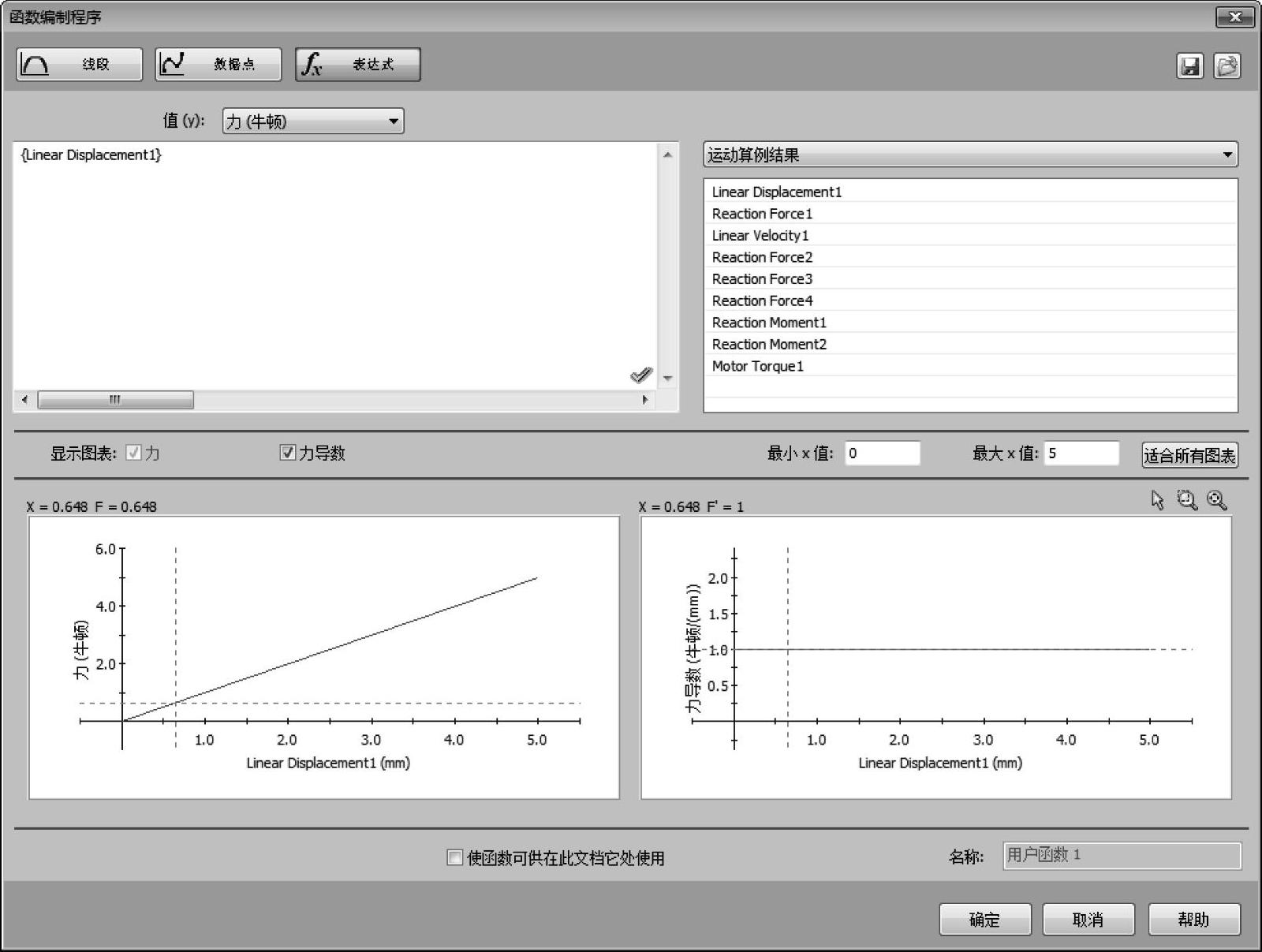
图12-20 定义力函数
步骤18 修改力
上面的力的初始值为-7.25N,是因为在仿真开始刀片分开的距离为7.25mm。当刀片的距离为零时力的大小为零。然而在仿真中,需要刀片相离3mm时的力为零(当刀片首先接触到导尿管时)。
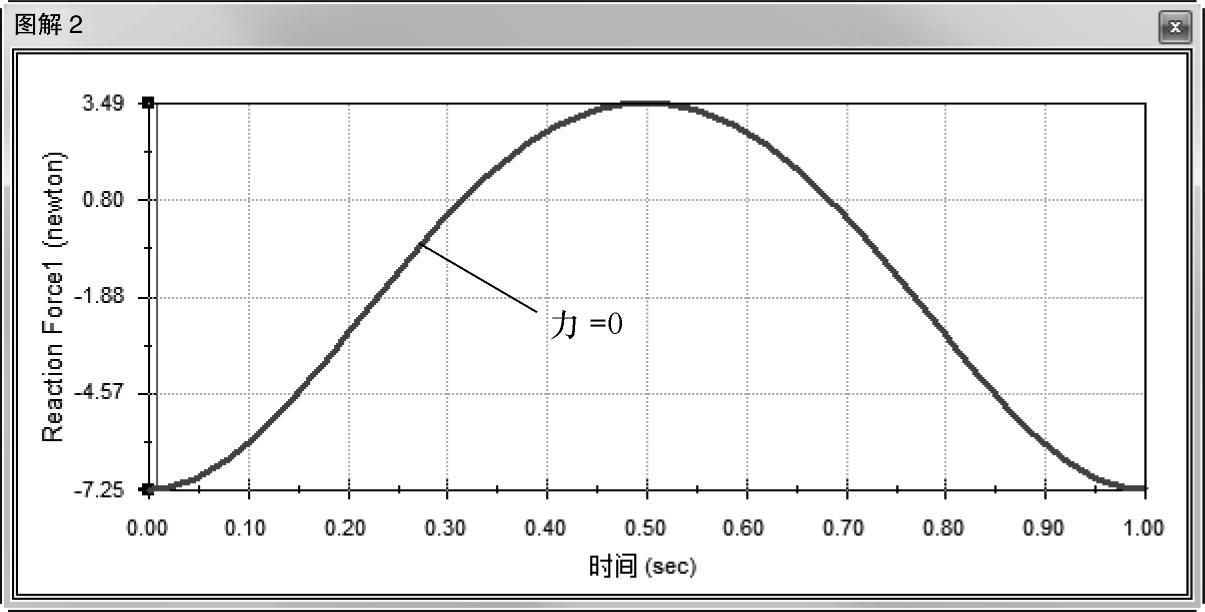
图12-21 查看图解(二)
将力的表达式改为“{LinearDisplacement1}+3”。
步骤19 重新运行仿真
现在,力的初始值为-4.25N,因为这个距离取自刀片和导尿管之间的距离。在刀片和导尿管接触时的力现在为零,如图12-22所示。
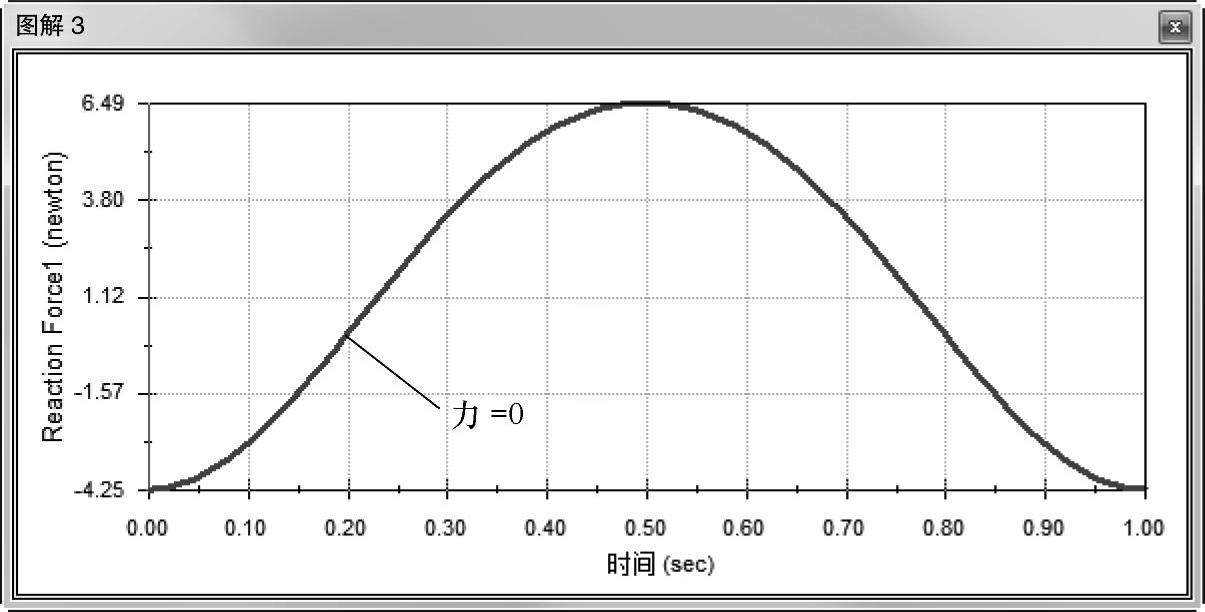
图12-22 查看图解(三)
注意
因此最后的一个表达式“{LinearDisplacement1}+3”定义了用于前面表达式中的X变量。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




