如何使用步进函数实现平滑过渡

步进函数表现了在给定数量（例如：位移、速度、加速度或力的大小）的两个数值之间具有光滑过渡。在过渡前后，位移、速度或加速度的大小是常数。

例如，考虑图4-6中的例子，其中：

d₀代表位移的初始值。

d₁代表位移的最终值。

t₀代表开始步长的时间。

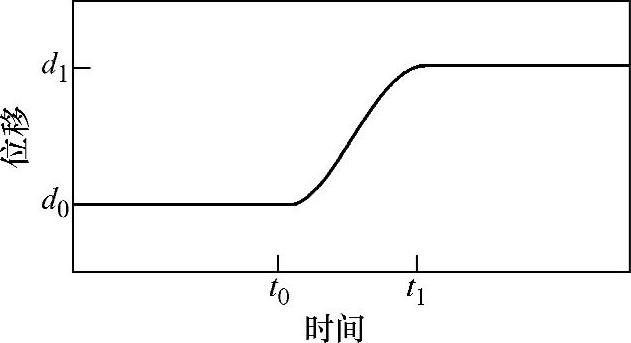
图4-6 步进函数

t₁代表结束步长的时间。

步骤8 生成一个旋转马达以驱动弹簧锁

隐藏J_Spring，在MotionManager工具栏中单击【马达】按钮。在【马达类型】中选择【旋转马达】。在【马达位置】或【马达方向】的任何一个选项中，选择Series Lever的Axis1。这次运动将模拟人手操作Series Lever来进行开锁和闭锁的动作，如图4-7所示。

在【运动】区域选择【表达式】，该命令将开启【函数编制程序】对话框。

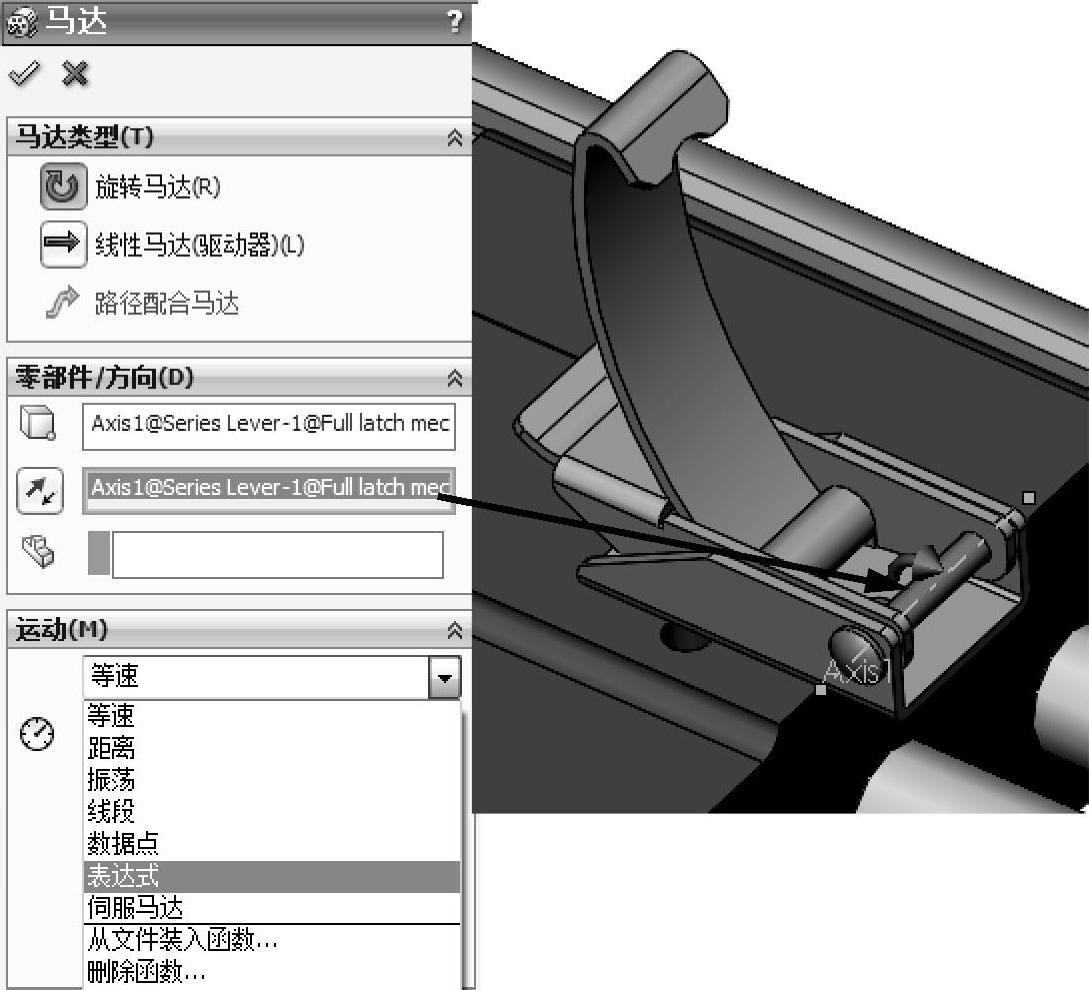
图4-7 定义旋转马达2

步骤9 创建马达表达式

在【函数编制程序】对话框中，确认选择了【表达式】按钮。输入类型处选择【数学函数】，双击【STEP（x，x0，h0，x1，h1）】以插入该步进函数。修改这个函数表达式为【STEP（TIME，0，0D，1，90D）】。

提示

变量TIME可以直接输入，也可以更改输入类型为【变量和常量】并双击【TIME】。

表达式完成的最终形式为STEP（TIME，0，0D，1，90D）+STEP（TIME，1.5，0D，3，-90D）(www.xing528.com)

提示

【函数编制程序】对话框将自动更新位移、速度、加速度和猝动的图解，如图4-8所示。

单击【确定】按钮，完成对表达式的定义并关闭【函数编制程序】对话框。单击【确定】按钮，完成对【马达】特征的定义。

提示

上面的表达式组合了两个步进函数。

第一个步进函数将使零部件Series Lever在0～1s转动90°，然后保持竖直的位置0.5s，直到1.5s。

在1.5s处，添加了第二个步进函数，即在1.5～3s将旋转位移改为0。

两个函数及其组合（Series Lever的最终运动）如图4-9所示。

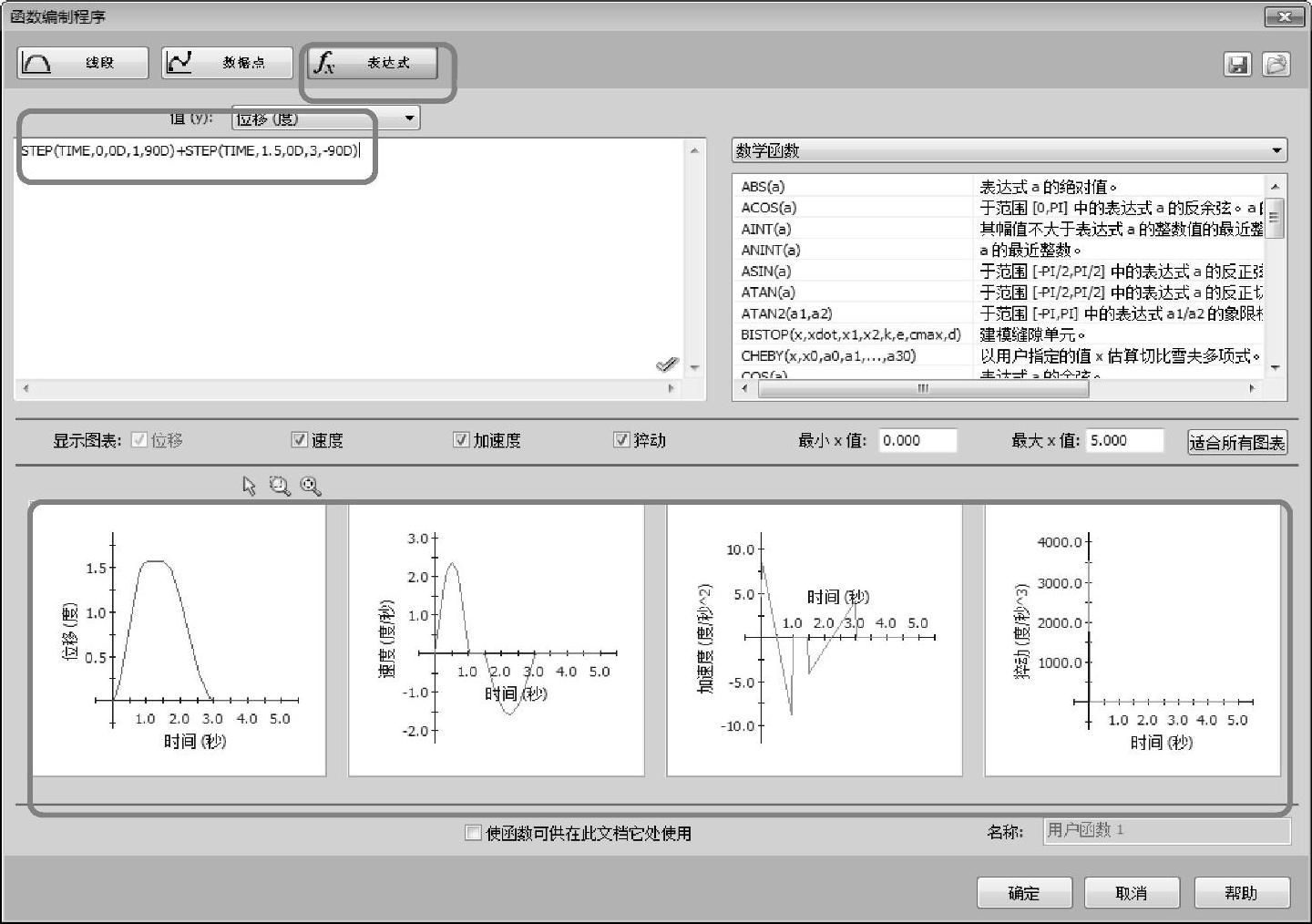
图4-8 【函数编制程序】对话框

步骤10 定义弹簧和阻尼

现在需要定义一个带阻尼的弹簧，以产生拉力将弹簧锁拉紧。在MotionManager工具栏中单击【弹簧】按钮。选择【线性弹簧】，【刚度系数】设定为“10.00牛顿/mm”，并在图4-10所示的位置创建弹簧。弹簧的自由长度将自动添加到【自由长度】选项中。

【自由长度】保持其默认值。勾选【阻尼】复选框，指定大小为“0.10牛顿/（mm/秒）”，如图4-10所示。单击【确定】按钮。

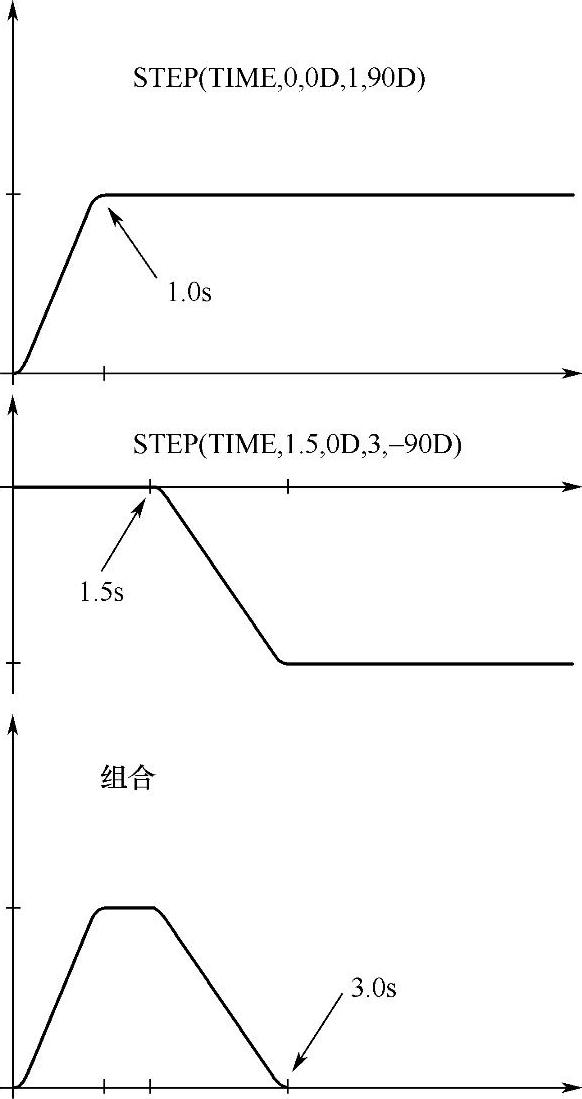
图4-9 步进函数

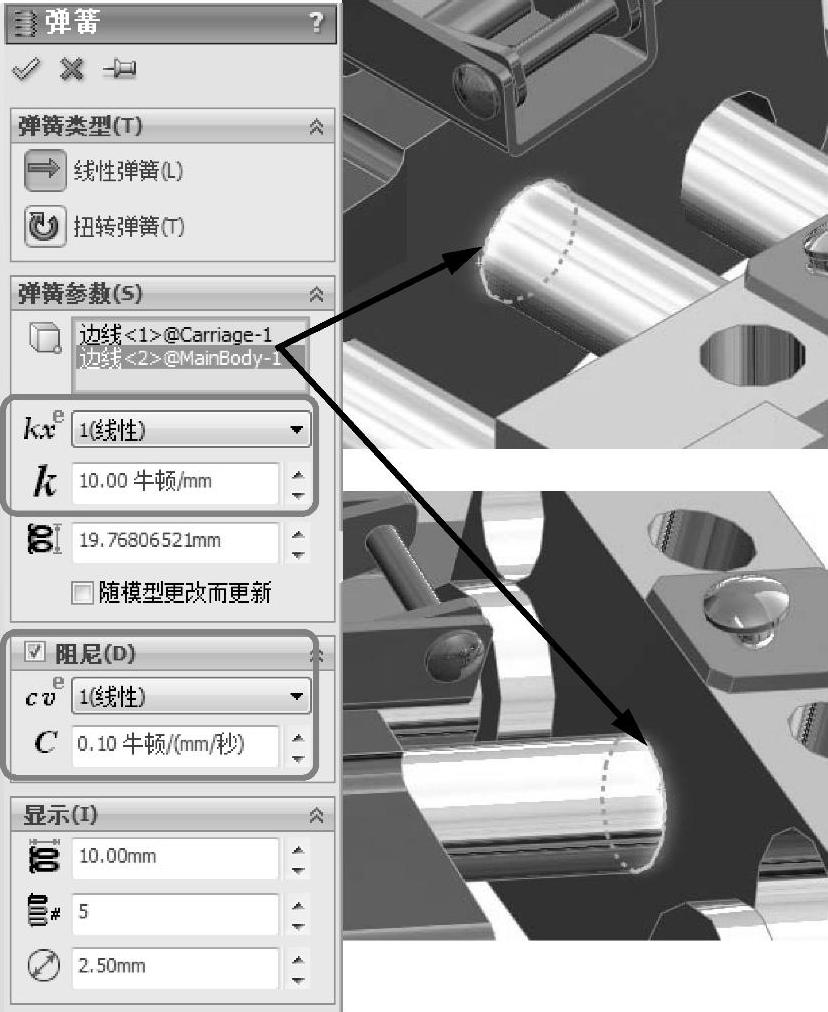
图4-10 定义弹簧和阻尼