能量（功率）是指功消耗的比率，或在1s内消耗的功的总量。力产生的功作用在距离、力矩、角位移上。对于旋转马达而言，需要保证下面的关系
P[W]=M[N·m]×ω[rad/s]
可以轻松解读前面生成的能量图解。最大力矩为10N·mm=0.01N·m
ω=360°/s=2πrad/s
可以通过生成角速度的图解来轻松验证这一点。最终的最大能量为：
P=（0.01×2π）W=0.063W
图中显示的能量为0.06W，这是因为默认只使用2位有效数字的精度。
通常电子马达的额定值可以由最大功率和力矩的表达式求得。单位换算也被频繁使用。
如果角速度单位为r/min，则
如果使用horsepower（马力），则将使用下面的转换
1hp=33000lb·ft/min=745.7W
当使用英制单位表示mechanical horsepower（机械马力）时，计算功率的公式为
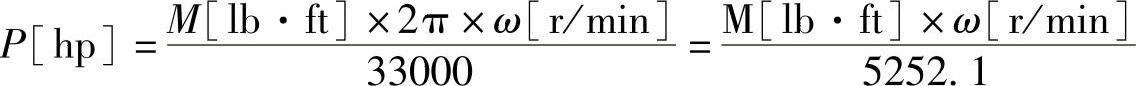
mechanical horsepower（机械马力）在美国的某些行业中应用非常普遍，除此之外主要用于欧洲和亚洲。还有Metric horsepower（米制马力），米制马力的定义如下
1hp=735.5W
由于定义马力的方式比较模糊，现在已经不再推荐使用马力了。
步骤25 运行算例
将【每秒帧数】调至“100”，重新计算该算例。
步骤26 查看结果
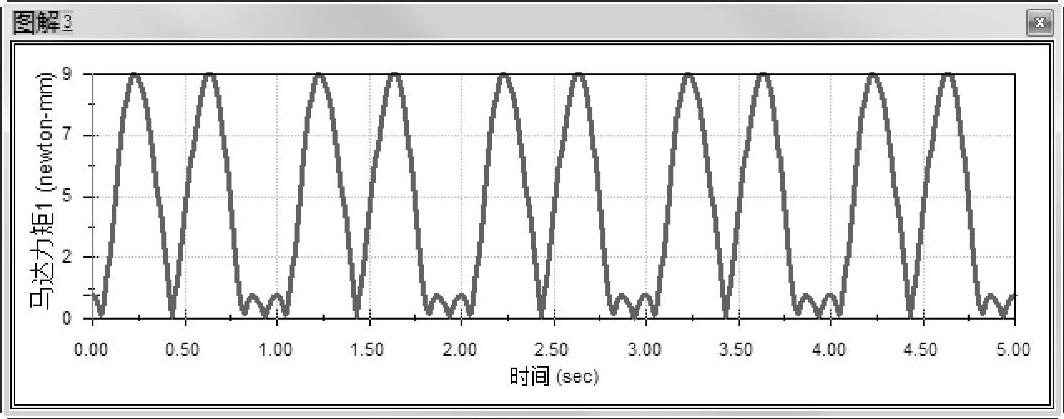
力矩的值在本质上和未添加【重合】配合时保持一致。图解看上去更加光滑，这是因为拥有4倍的数据点，如图2-29所示。
(www.xing528.com)
图2-29 查看图解
步骤27 图解显示反作用力
新建一个图解，显示马达的反作用力。选择【力】、【反作用力】、【幅值】定义该图解。在这个装配体中，定义的第一个铰链位于crank和crank_hous-ing之间。因为crank_housing是固定的，配合就必须传递反作用力。
在【模拟单元】中选择第一个铰链配合。由于所选的配合连接两个零件，所以存在两个相等且反向的力作用在这个配合上。必须选择两个零件中的其中一个来生成这个力的图解。
在【模拟单元】中选择零件crank-1中的任意表面为第二个成分。勾选【在图形窗口中显示向量】复选框，如图2-30所示。单击【确定】。
提示
必须从Motion Manager设计树中选择该配合，因为该配合为本地配合，因此不会显示在FeatureManager设计树中。
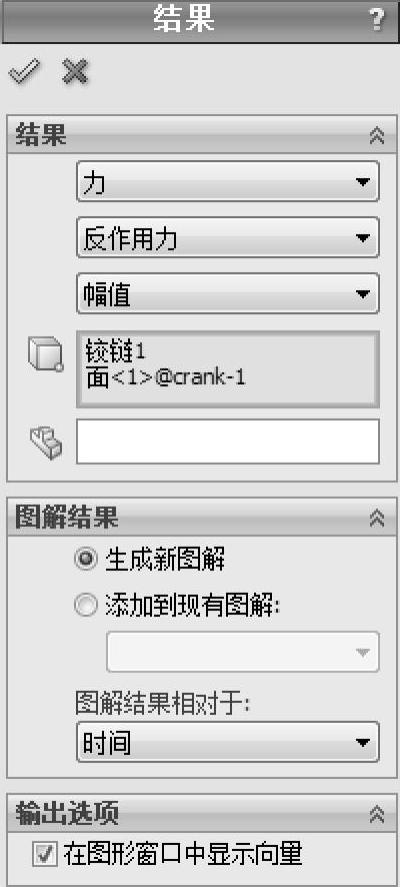
图2-30 定义反作用力图解
步骤28 警告
这时将收到关于冗余约束的警告，如图2-31所示。冗余约束可能会对配合的力（由配合定义的机械连接的力）产生重大影响，具体将在本书后面的部分进行讨论。然而，这个机构中得到的合力是正确的，因为这个装配体中出现的冗余并不会对图2-32中的力产生影响。单击【否】。
步骤29 查看图解
播放这个仿真，观察反作用力的变化，如图2-32所示。
图2-31 警告
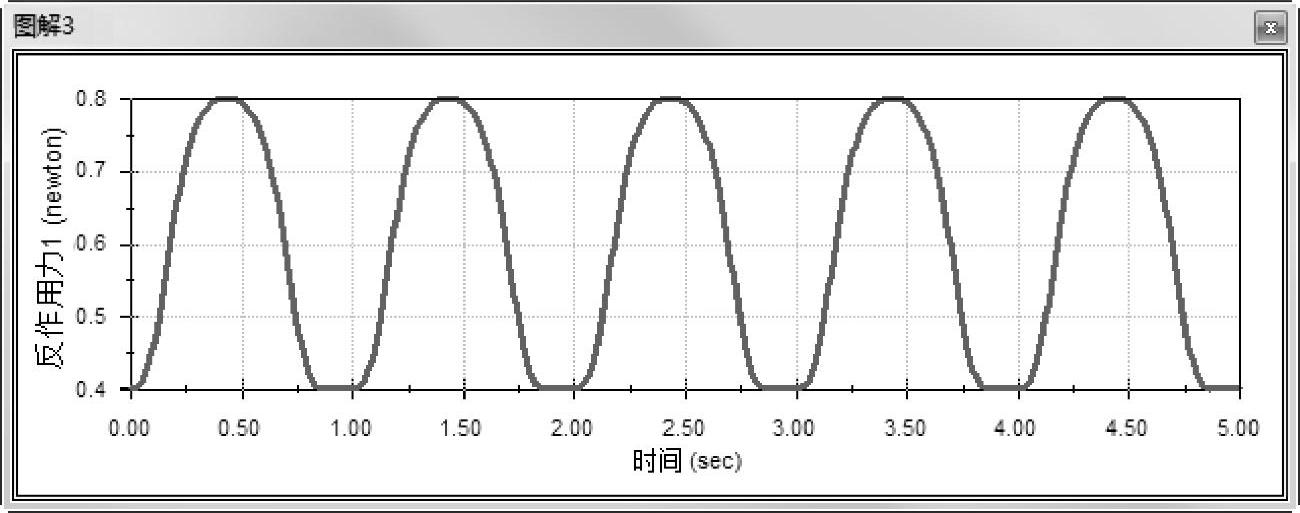
图2-32 查看反作用力图解
从右视图中观察到的结果如图2-33所示。
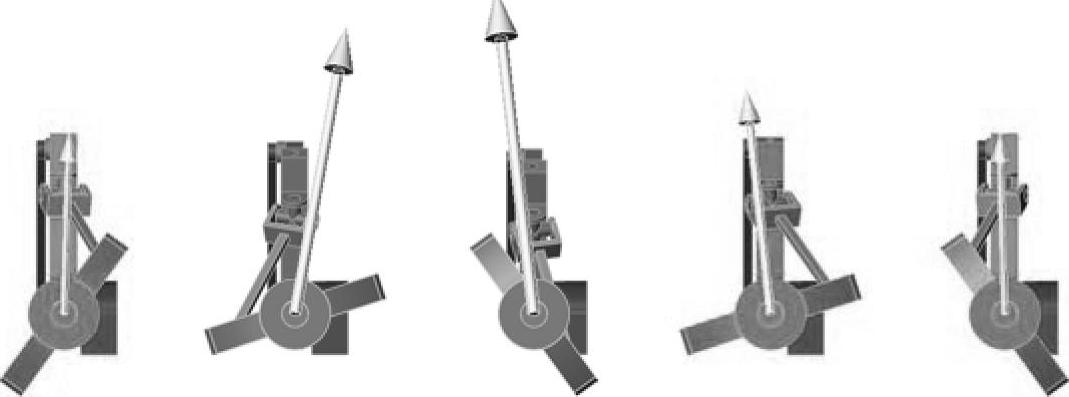
图2-33 右视图结果
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
