【摘要】：质量与惯性 惯性定律是经典物理学基本定律之一，它描述了力与运动的关系。约束自由度 减少自由度将限制构件的独立运动，这种限制称为约束。如图0-2所示，配合连接两个构件，并限制两个构件之间的相对运动。对质量不发生改变的实体，方程式右侧可以简化成更为大家熟知的质量乘以加速度，ΣF=ma。运算结果不断迭代直到满足预定的精确度，如图0-3所示。
（1）质量与惯性 惯性定律是经典物理学基本定律之一，它描述了力与运动的关系。现在，惯性的概念通常用牛顿第一运动定律描述：
一切物体总保持匀速运动状态或静止状态，直到有外力迫使它们改变这种状态。
在动力学和运动学系统的仿真过程中，质量和惯性有非常重要的作用，几乎所有的仿真过程都需要真实的质量和惯性数据。
（2）自由度 一个不被约束的刚性物体在空间坐标系中具有6个自由度：3个为平移自由度，3个为转动自由度。如图0-1所示，它能够沿X、Y和Z轴移动，并绕X、Y和Z轴转动。
（3）约束自由度 减少自由度将限制构件的独立运动，这种限制称为约束。如图0-2所示，配合连接两个构件，并限制两个构件之间的相对运动。
图0-1 自由度
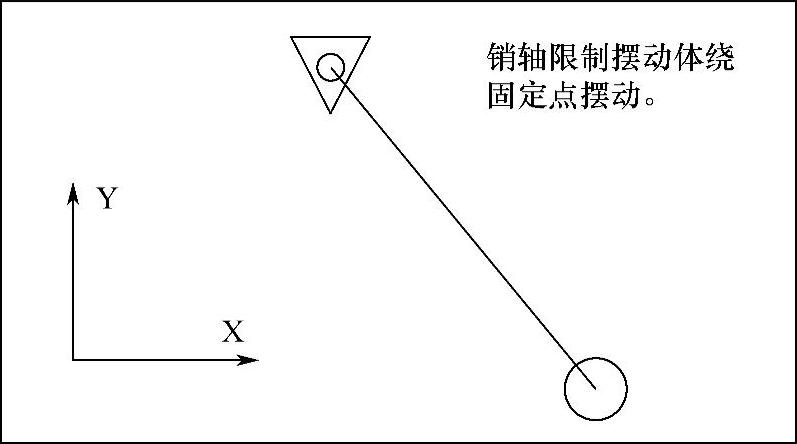
图0-2 约束自由度
（4）运动分析 欧拉方程说明了一个刚性物体的三维运动规律，它由两个方程组成：第一个方程是牛顿第二运动定律，它描述了施加在主体上外力的总和等于线动量p的变化率，即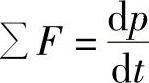
。(https://www.xing528.com)
对质量不发生改变的实体，方程式右侧可以简化成更为大家熟知的质量乘以加速度，ΣF=ma。第二个方程说明主体上外力围绕质心产生力矩之和等于主体角动量H的变化率，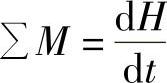
。
（5）运动分析步骤 在每个时间步长中，程序使用改进的Newton-Raphson迭代法进行求解。通过非常小的时间步长，根据零件的初始状态或前一时间步长的结果，软件可以预测下一时间步长内零件的状态，但求解时必须已知以下量：
● 构件速度。
● 连接构件的配合。
● 力与加速度。
运算结果不断迭代直到满足预定的精确度，如图0-3所示。
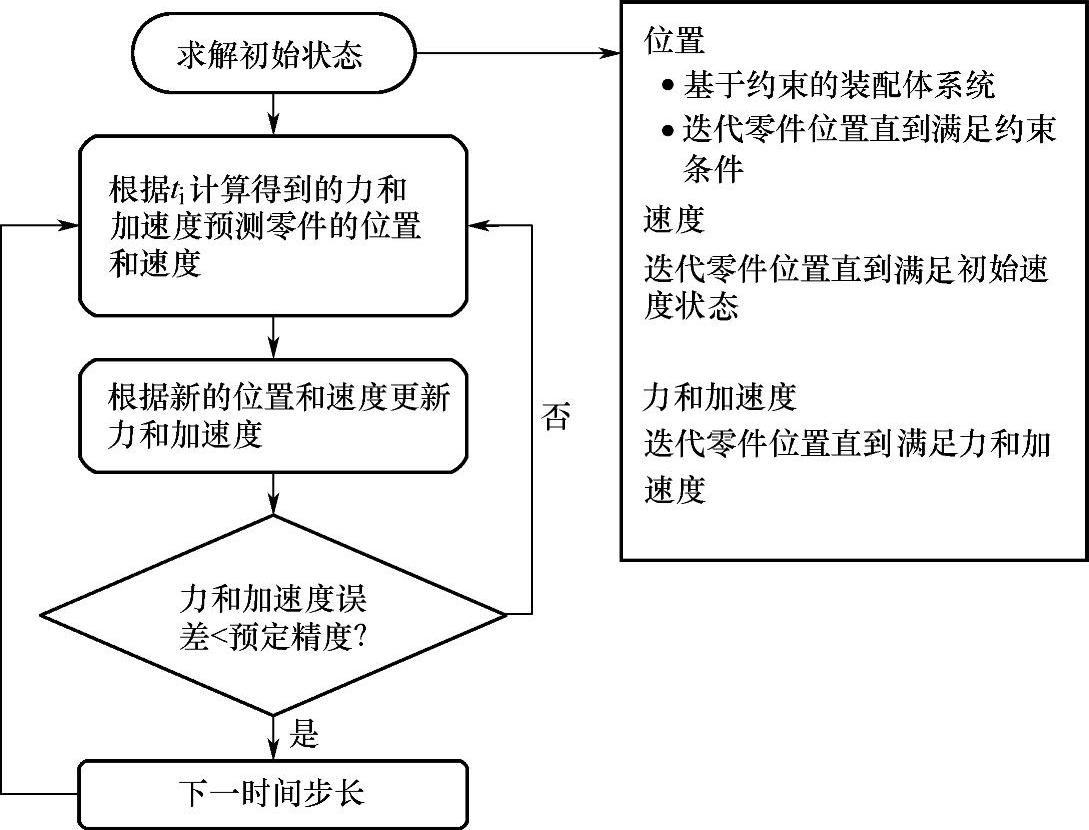
图0-3 分析步骤
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
