动态相似性评估方法优化

一、动态时间规整

动态时间规整（DTW）是一种衡量两个不同长度的时间序列的相似度的方法，可以用于语音识别、手势识别、数据挖掘、信息检索等方面。对于机器鼠而言，其在运动过程中的某一参数即可以看做是一个时间序列。同样地，实验鼠的对应参数也是时间序列。因此，可以采用DTW的方法来衡量两者在动态运动过程中的相似程度。

动态时间规整的思想如下[2]：假设有两个时间序列QNs和CMs，其序列长度分别为Ns和Ms。Q序列和C序列一个作为参考模板，另一个作为测试模板，序列中的每一个点值为机器鼠或实验鼠的运动参数，即

QNs={q1,q2,…,qNs}

CMs={c1,c2,…,cMs}

首先，构造一个Ns×Ms的矩阵网格，其矩阵元素（i，j）表示qi和cj两个点的距离d（i，j），因此，该矩阵表示了序列QNs的每一个元素与序列CMs中每一个元素之间的距离。通常，这个距离取为欧几里得距离，即

然后，需要找到一条最优的路径，来“规整”两个序列，使Q与C在路径上“对齐”。我们定义这条最优的路径为WKw，长度为Kw，WKw的第k个元素为wk=（i，j）k，表示了序列Q与序列C的映射关系，即

需要注意的是，这条路径并不是随便选择的，需要满足以下几个约束条件：

（1）边界条件。w1=（1，1），wKw=（Ns，Ms），即规定了路径的起点和终点。

（2）连续性。如果wk-1=（i′，j′），那么对于路径的下一个点wk=（i，j）需要满足（i-i′）≤1且（j-j′）≤1。

（3）单调性。如果wk-1=（i′，j′），那么对于路径的下一个点wk=（i，j）需要满足（i-i′）≥0且（j-j′）≥0。

在满足上述约束的条件下，动态时间规划的一个可能路径如图6-8所示。但是，这样的路径并不唯一，而我们感兴趣的是规整代价最小的路径，即满足下式的路径：(www.xing528.com)

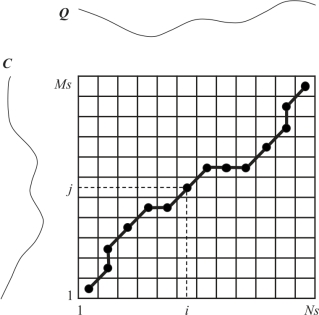
图6-8　DTW及路径示例

为此，可以通过计算累积距离获取最优路径。下面，将矩阵（i，j）处的累积距离定义为γ（i，j）（见式（6-15）），即当前格点距离d（i，j）与可以到达该点的最小的临近元素的积累距离之和：

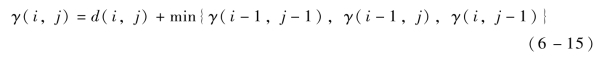
最佳路径即为使得沿路径的累积距离达到最小值的这条路径。这条路径可以通过动态规划算法得到。

二、机器鼠动态相似性

我们分析了实验鼠BP-Ⅰ和BP-Ⅱ（见5.3.1小节）两种情况下机器鼠运动的动态相似性。在这两种情况下，以实验鼠和机器鼠的俯仰高度hp为例，将BP-Ⅰ和BP-Ⅱ过程中该量的变化看做两组时间序列：实验鼠的俯仰高度序列作为参考序列，机器鼠的俯仰高度序列作为测试序列。为了验证DTW作为动态相似度评估的有效性，控制机器鼠以正常速度（test1）和慢速（test2）分别实现BP-Ⅰ和BP-Ⅱ运动，并最终计算出了它们的比较结果，如图6-9和图6-10所示[3]。

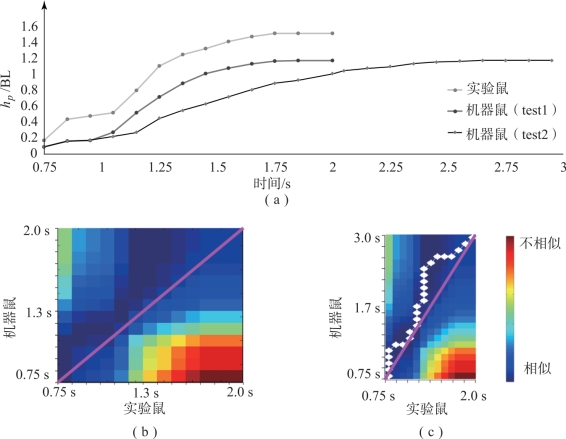
图6-9　BP-Ⅰ动态相似度比较（见彩插）

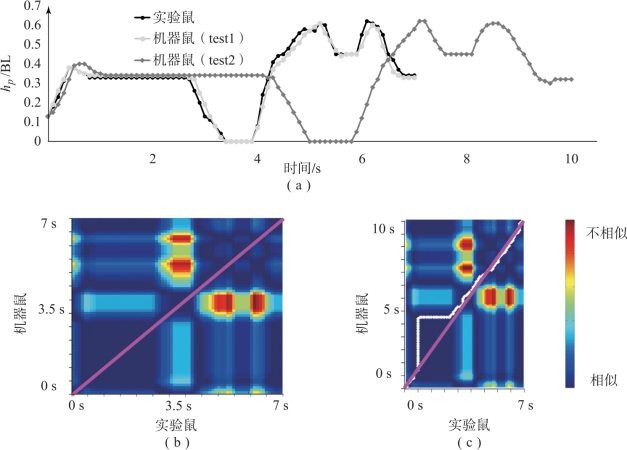
图6-10　BP-Ⅱ动态相似度比较（见彩插）

由图6-9（a）和图6-10（a）可以发现，test1的曲线与实验鼠相比具有相似的趋势，而test2的曲线在一定程度上被拉长，这是由于机器鼠以慢速执行的缘故。仅从曲线形状上看，机器鼠test1曲线与实验鼠的曲线是相似的。但是，机器鼠test2曲线与实验鼠的相似性就比较难以判断。此外，上述判断都是主观性的判断，因而仍然需要一些定量指标来评估该相似程度，DTW方法正好解决了上述问题。DTW比较的最终结果如图6-9（b）和（c）以及图6-10（b）和（c）所示。在图中，矩阵块的不同颜色表示实验鼠与机器鼠运动时间序列之间的欧式距离，白道线表示DTW的最佳路径。根据该结果，BP-Ⅰ的DTW累积距离分别为0.574 1（test1）和0.605 8（test2），而BP-Ⅱ的DTW累积距离分别为0.019 2（test1）和0.025 2（test2）。显然，BP-Ⅰ的累积距离远大于BP-Ⅱ的累积距离。这意味着，机器鼠在执行两个不同的动作时，BP-Ⅱ具有比BP-Ⅰ更好的相似性。同时，在正常速度和慢速测试中，两者的累积距离值几乎相等，表明DTW方法对不同的运动速度不敏感，从而可以忽略机器鼠运动的速度，而只关注于机器鼠与实验鼠的运动相似性。

此外，DTW的最终结果还可以帮助我们确定机器鼠与实验鼠的最相似处或最不相似处。以图6-10（b）为例，紫色对角线表示理想的最优路径，表示机器鼠的运动与实验鼠严格相同。当白色的实际最优路径和紫色理想最优路径越接近时，则表示此时机器鼠与实验鼠的运动越相似；反之，当白色线与紫色线距离越大，则表示机器鼠与实验鼠的运动在该时刻越不相似。在图6-10（b）中，白色线和紫色线之间的距离在0.8～2.6 s时达到最大值。这意味着，在此期间机器鼠的行为与实验鼠的行为有较大的不同。由此，可以根据比较结果有针对性地改进机器鼠的控制，从而使得机器鼠的运动最大化地与实验鼠的运动相似。