轮式机器鼠俯仰与偏航运动稳定性分析

一、俯仰运动

机器人系统的稳定性是衡量机器人动态性能的重要指标之一。在分析轮式机器鼠俯仰运动的稳定性时，不仅要求其在运动过程中不发生倾覆，而且具有更为严格的约束，即在俯仰运动过程中不产生振动（轮子瞬时脱离地面）。建立机器鼠俯仰运动动力学模型如图6-3所示。机器鼠有n（i=1，2，…，n）个旋转关节，从侧面看，其主体可以简化为n个连杆和一个车轮（底座）部件（前：被动轮，后：主动轮）。

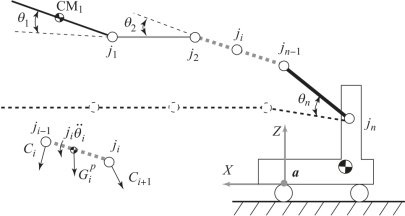
图6-3　机器鼠俯仰运动动力学模型

考虑俯仰运动上升过程中机器鼠临界稳定的情形。此时，机器鼠后轮处的支持力为零。推导作用于a点的总力矩Mp，它由惯性矩、离心力与科氏力矩和重力矩三部分组成，为了防止机器人在俯仰运动中产生振动，应满足以下约束方程：

其中，jy表示y轴的单位方向矢量。取决于四个俯仰关节运动的角加速度。根据牛顿第三定律，连杆的旋转将对车轮部分产生反作用力，可以表示为：

其中，θp=[θ1θ2…θn]T，关节角位移变量应遵循上述得到的机器鼠仿生运动规律。Jp=[J1J2…Jn]，J1为连杆1绕旋转关节1的转动惯量，J2为连杆2绕旋转关节2的转动惯量，Jn为连杆n绕旋转关节n的转动惯量。则取决于各俯仰关节运动的角位移和角速度，可以表示为：

其中，Ci为由于作用于连杆i的离心力与科氏力的合力（如图6-3所示），ri为a点到关节点ji-1的矢径。为了简化对于的计算，我们通过仿真估计其数值范围。在ADAMS软件中建立与机器鼠WR-5M对应的机械模型，使机器鼠各连杆以恒定角速度绕各俯仰关节旋转，得到各关节之和的变化曲线如图6-4所示。为了保证机器鼠的运动稳定性，我们取其中的最大值参与到机器鼠的稳定性分析当中。则由机器鼠的n个连杆和底座部分产生，显然，底座部分的重力矩在俯仰运动过程中是恒定值。由各连杆重力（i=1，2，…，n）以及a点到各连杆质心处的矢径riG可以得到重力矩，即：

对于俯仰运动下降过程中的稳定性条件，可通过上述方法对b点取矩类似得到。

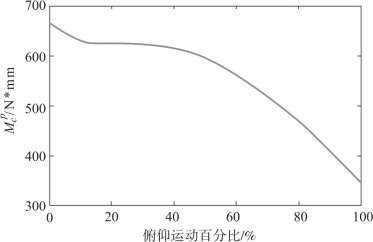
图6-4　机器鼠俯仰运动过程中的离心力与科氏力矩

二、偏航运动(www.xing528.com)

在分析轮式机器鼠偏航运动的稳定性时，要求在偏航运动过程中不发生侧滑（侧滑条件严格于振动/倾覆条件，故仅考虑侧滑约束）。建立机器鼠俯仰运动动力学模型如图6-5所示。机器鼠有k（i=n+1，…，n+k）个旋转关节，从上面看，其主体可以简化为k个连杆和一个底座部件。

机器鼠有两个脚轮（a点和d点）以及两个橡胶轮（b点和c点）与地面接触。每个点可提供的最大静摩擦力可由静摩擦系数与该点处支持力的乘积表示，即有fa=μaNa，fb=μbNb，fc=μcNc，fd=μdNd。Fco为作用于各连杆Ci（i=n+1，…，n+k）的合力。在偏航运动过程中，机器鼠容易在接触点滑动。当四个接触点中的任何一个产生滑动时，都会破坏机器鼠的稳定性。此时，施加在机器鼠上的偏航主动力超过了接触点所产生的最大静摩擦力。由此可得机器鼠在偏航运动过程中保持稳定的条件为：

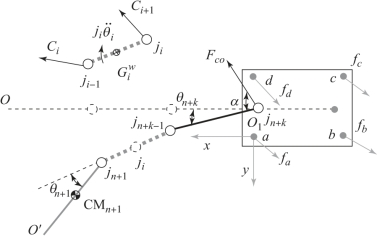
图6-5　机器鼠偏航运动动力学模型

为了进一步解析由式（6-7）所示的平衡条件，需要得到Na、Nb、Nc、Nd的表达式。列写x-y平面内的力矩平衡方程（对o1点取矩）：

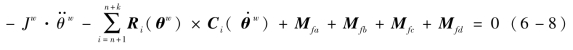
其中

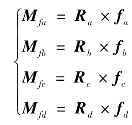
θw=[θn+1　…　θn+k]T，关节角位移变量应遵循上述得到的机器鼠仿生运动规律。Jw=[Jn+1，…，Jn+k]，Jn+1为连杆n+1绕旋转关节n+1的转动惯量，Jn+k为连杆n+k绕旋转关节n+k的转动惯量。Ri为o1点到关节点ji-1的矢径，Ra、Rb、Rc、Rd分别是o1点到a、b、c、d点的矢径。类似地，可列写x-z平面和y-z平面的力矩平衡方程：

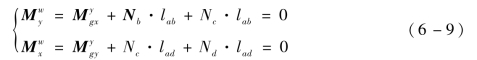
其中

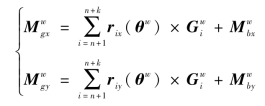
rix与riy分别为x-z平面和y-z平面内a点到连杆i质心处的矢径。在机器鼠偏航运动过程中，机器鼠在z轴方向的加速度为零。由此，易得沿z轴方向的力平衡方程：

通过式（6-8）～（6-10）可得到由关节角位移变量θw表示的Na、Nb、Nc、Nd。