一、CPG生物机理及模型
动物行为中节律性运动是由低级神经中枢如中枢模式发生器(CPG)神经网络控制的一种自激性行为。动物的节律运动有很多种,如行走、奔跑、游泳等运动,在运动中其脊柱中的CPG神经单元会直接对这类节律运动进行控制而不经过高层神经中枢。此外,效应器官(如腿、肌腱等)的运动可以直接由CPG输出的信号控制,而从高层神经中枢(如大脑)向CPG中枢神经传输的信号仅起到初始化的作用而不直接产生任何运动效果。对于外界的刺激,CPG中枢会做出如同高层神经网络一样的反射活动,对自身产生的电信号进行修正来适应于环境的变化。此外,在无外界环境刺激时,CPG中枢同样会继续工作。换言之,CPG协调节律运动是不需要借助反射活动或外部输入传感信息,神经元同样会产生周期性活动[16]。
二、基于CPG网络的步态规划
CPG振荡模型种类较多,如Hopf振荡器模型、Kuramoto模型以及Matsuoka模型等[17]。这其中基于Matsuoka模型的CPG神经元结构的生物意义较为明确,因此在机器人步态规划中应用比较广泛。Taga等人在面对控制双足机器人的问题时,利用两个Matsuoka神经元模型组成一个单元控制一个关节,并且关节运动的控制是根据两个神经元的兴奋和抑制程度来实现的,最后用6个振荡单元完成了对机器人的控制[18]。图5-37所示为Kimura等人为了避免Matsuoka模型存在的只有正值输出的问题,而提出的神经元单元模型,该模型的单元输出是由代表屈肌和伸肌的控制神经元的输出相减得到的,从而解决了该问题[19]。
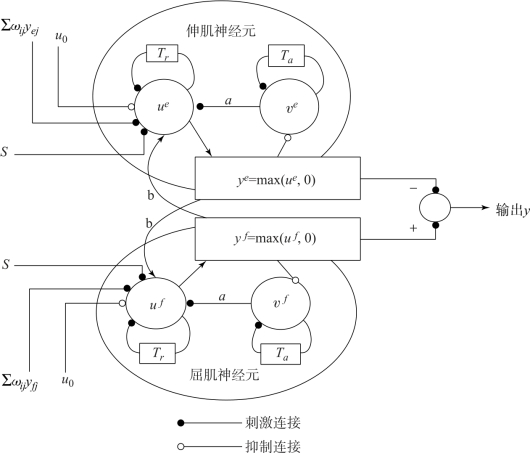
图5-37 基于Kimura模型的CPG振荡单元[19]
振荡单元是由Kimura模型中互相抑制的两个神经元构成的,并且由4个振荡单元组成CPG神经网络。这4个振荡单元分别代表四足机器人的4条腿,它们两者之间的连接方式均是双向的。当ωij为正值时,相互连接的两个振荡单元的连接处于兴奋状态;当ωij为负值时,相互连接的两个振荡单元的连接处于抑制状态。通过改变振荡单元连接权重的正负值就可以改变为其他步态,实现不同步态之间的转换,这也是CPG控制常用于四足机器人控制的优势之一。
振荡单元i(i=1,2,3,4)的数学模型如下:

式中,e、f分别为伸肌(extensor)运动神经元和屈肌(flexor)运动神经元;u为神经元内部状态;v为神经元自抑制状态;y和y{e,f}分别为振荡单元和神经元输出信号,这两个变量可作为实际的关节控制量;Tr和Ta分别为上升时间系数和适应时间系数,分别说明神经元阶跃响应的上升时间和神经元适应效果的滞后时间;α和β为神经元适应系数和振荡单元互抑制系数;ωij为振荡器j对i之间的连接权重;Fik为外部刺激k对振荡单元i的反射输入,是反馈输入项;hk为反射系数;s为高层的神经中枢(如大脑)的刺激输入,通常情况下所有神经元的输入相同;g(u)为一种阈值函数,阈值C取零值,但实际情况可根据需求进行设定。
步态矩阵定义了每个振荡单元的耦合模式。四足机器人最常见的4种步态是步行、小跑、踱步和双足跳跃。其中,除了步行属于四拍步态外,其他3种均为双拍步态。在步行步态下,其网络的任意两两振荡单元构成的连接对均处于抑制状态;对于双拍步态,在任意1个振荡单元与其他3个单元构成的连接对中,仅有一对连接处于兴奋状态;另外两对连接处于抑制状态。4种不同步态下的步态矩阵如下:


三、关节驱动函数设计
在保持频率和振幅的条件下,4个振荡器在步行步态中的输出经过上述的参数整定过程实现了稳定的输出。考虑到机器鼠肩关节和髋关节在行走时呈现明显的周期性摆动,可以将CPG网络的4个输出信号作为肩关节和髋关节的驱动函数。由于动物在行走过程中,前肢的肘关节和肩关节以及后肢的膝关节及髋关节的运动存在固定的相位关系,因此使用关节映射函数(见式(5-58))作为驱动肘关节和膝关节的关节驱动函数。该函数为经典的CPG信号的映射函数,广泛应用于足式机器人的研制过程中[20]。
关节驱动函数可定义为

式中,θ{s,h}和θ{e,k}分别为肩/髋关节和肘/膝关节控制信号;A{s,h}和A{e,k}分别为肩/髋关节和肘/膝关节振幅值。
此外,该函数产生的肘关节/膝关节控制信号在摆动阶段移动,在支撑阶段不移动。图5-38为步行步态中所有关节输出的模拟曲线。利用这种控制策略,可以将CPG网络的输出和映射功能应用于驱动整个机器鼠。
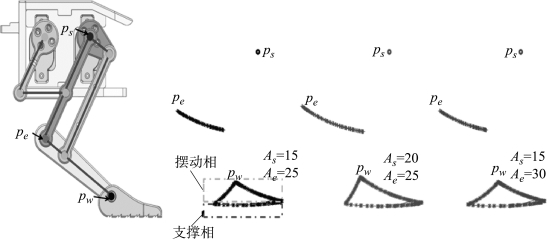
通过CPG网络得到各关节的控制信号,就可以获取其足端轨迹的信息。可以看出,机器鼠的跨步长度由肘关节的运动决定,而肩关节的作用则是提高摆臂的高度。如图5-39所示,得到的足端轨迹曲线具有平滑、无尖点、无突变的特点,而且支撑相轨迹接近直线利于机身稳定,摆动相抬脚较高不会产生脚拖地的现象。此外,通过分析CPG网络的输出轨迹的相轨迹图,由图可以看出,CPG网络的输出随时间变化最终稳定收敛在极限环内,如图5-40所示。
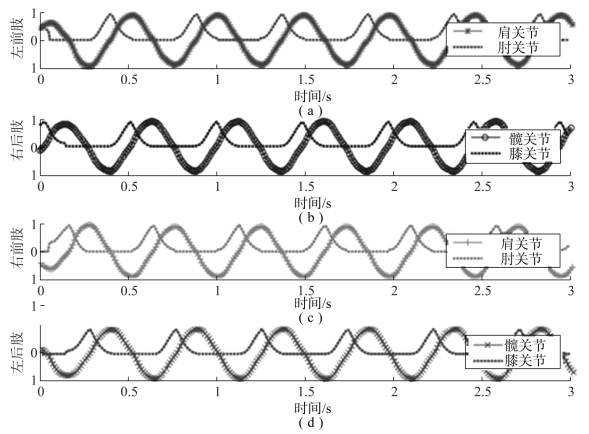
图5-38 机器鼠步行步态下控制关节的输出曲线
(a)左前肢;(b)右后肢;(c)右前肢;(d)左后肢
 (https://www.xing528.com)
(https://www.xing528.com)
图5-39 机器鼠在不同幅值信号下的足端轨迹曲线
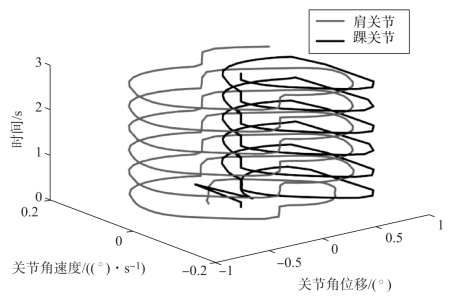
图5-40 CPG网络的关节输出量的相轨迹图(见彩插)
四、CPG参数优化
在实际控制过程中,控制程序是时间离散的差分方程,对上述基于Kimura模型的CPG振荡单元方程进行离散化处理,得到CPG中枢神经离散方程。在实际运算中,对于差分方程的精确求解通常使用高阶龙格-库塔法。但是,在参数整定过程中,由于不需要过于精确地求值,所以使用欧拉法和中值定理来进行振荡曲线的仿真。由于求解的是改写后的差分方程,因此存在差分方程数值解与原方程真实解的误差问题。为了降低误差,将Tc值取为0.01,并忽略外部信息对振荡单元的输入,由此建立的行走步态下的数学模型如下:

粒子群优化算法(PSO)是由Eberhart等人发明的一种基于群体智能的进化计算方法[21]。该算法是一种基于迭代计算的优化工具,其最先启发于鸟类的觅食活动,是一种种群式优化算法。该算法在大类的智能算法中依然属于一种进化算法,对比其他遗传和免疫等进化算法,其具有更少的超参数,不需要很多的调参经验便可以得到很好的结果的优点,因而得到了广泛的应用。其工作流程为:初始化所有的粒子(随机生成),每个粒子在一次迭代中随机选取方向得到新的解,并综合所有粒子的解比较得到本次迭代中所有粒子找到的最优解,该最优解的位置为gbest,标定的最优解作为粒子群的全局最优解。每个粒子都会了解到这个全局最优解,在下次迭代时也会趋于上次找到的最优解。对于每个个体粒子来说,除了参考全局最优解,还会记录自己在过程中所找到的个体最优解的位置gbest,在更新时会同时考虑这两点,然后更新其速度v和新位置ppresent,这使得系统具有较强的稳健性,不会陷入局部最优,则
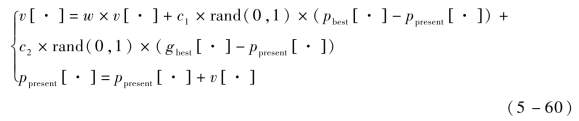
式中,v[·]为粒子的速度;ppresent[·]为粒子的位置;rand(0,1)为生成的随机数;c1、c2是学习因子;w为惯性权重。
PSO中并没有许多需要调节的参数,大多可靠经验设置,并参考CPG参数整定特殊性,可以优化选择参数值。
(1)粒子数。粒子数一般取20~40。粒子数有时会取100~200,这是因为对于比较难的问题或者某些具体的问题,粒子数太少会找不到最好的结果。对于机器鼠腿部CPG模型的参数整定,取常用值20。
(2)学习因子。对于学习因子,一般取c1等于c2,且范围应该在4以内。对于CPG参数整定,粒子的移动速度不需要很快,所以选择了较小值,c1=c2=0.6。
(3)惯性权重。惯性权重取值为0.9时利于寻找全局最优;当寻找局部最优时,惯性权重一般为0.4。由于CPG参数耦合的特殊性,如果粒子得到较优解时,在周围搜索一般即可得到更优的解,所以惯性权重为0.4。
(4)最大速度Vmax。最大速度是粒子在单次循环中移动速度的最大值。在参数整定中,它的作用是限制各粒子的移动速度,防止在参数整定过程中漏过最优解。
在具体的控制过程中,Tr和Ta的取值是相互联系的,一般有Tr=Ta/10,这样可以获得较好的振荡曲线。因此,依据经验选择Ta、α、β、s这4个参数来进行整定即可,而Tr则由上述规律可以得到。由于在试凑过程中,发现Ta的取值范围一般不超过1,所以在整个PSO算法中,把Ta的求解粒子的速度最大值做了限制。但是,α、β、s 3个值的变化范围较大,为了防止其快速收敛于局部最优,同时扩大其搜索速度,经多次尝试发现限制求解Ta最大速度为1,限制求解α、β、s的最小速度为0.03会让整个过程快速收敛于理想的解。对于CPG模型控制:首先要得到稳定的预设频率和幅值的振荡曲线;其次得到的曲线起振时间越短越好。对于频率和幅值的求取,由于输出曲线需要频率和幅值均达到较优,涉及多目标的参数整定,所以设置实际输出曲线的幅值x和频率y与目标幅值xT和频率yT之间的距离D为损失函数(见式(5-61)),实现同时对幅值和频率两个目标的优化求解。此外,机构及驱动的限制所施加的约束条件为频率y0(0>y0<4 Hz)时
![]()
CPG控制步态选择小跑步态时,目标频率选择3 Hz,目标幅值选择6,该参数用来检验CPG优化的效果。利用PSO算法,迭代1 000代后得到结果。输出波形稳定,得到其优化后的振荡频率为2.963 Hz,幅值为5.988 5。目标频率和幅值误差在可接受的范围内。优化后的CPG参数如下:
Tr=0.011 93,Ta=0.109 3,α=1.029 9,β=1.076 4,s=1.181 7
CPG控制步态选择步行步态时,目标频率为3 Hz,目标幅值为6。利用PSO算法,粒子数为20,学习因子为0.6,惯性权重为0.4,迭代1 000代后得到结果。输出波形稳定,但在2 s后才真正达到完全的振荡。得到稳定振荡后其优化的振荡频率为3.157 9 Hz,幅值为6.074 4。频率和幅值误差在可接受的范围内。优化后的CPG参数如下:
Tr=0.018 17,Ta=0.141 7,α=3.718 3,β=1.350 7,s=7.271 5
对于步行步态,同时要求起振时间越短越好。可以发现,整定后的输出曲线各单元输出稳定的时间不同,最后大部分都会稳定振荡。对于初值的选取,采用的是先将前一步优化得到的Tr、Ta、α、β、s 5个参数确定,再将其稳定输出后的ue、uf、ve、vf带入CPG控制模型中,将其作为CPG控制初值的方法,这样即可得到稳定输出的曲线。整定初值后的输出曲线(图5-41(a))与未整定初值的输出曲线(图5-41(b))相比可以实现更为快速的振荡[22]。
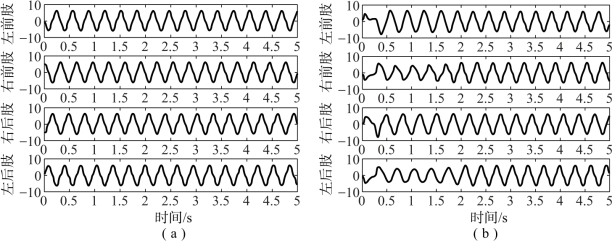
图5-41 CPG输出曲线对比
(a)整定初值后;(b)未整定初值
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




