稳定性分析与检测

由足式机器鼠的机械结构，可以构建简化的双倒立摆及柔性腰部模型，如图5-36所示。对该模型进行基于李雅普诺夫方法的稳定性分析，可以得到机器鼠直线行走及转弯时的稳定性判据，指导其后续的步态规划。根据机器鼠机械结构的特点，将机器鼠整体划分为前肢、腰部和后肢3个模块。由于前、后肢的设计是相似的，且双足机器人常采用倒立摆简化模型[13]，所以这两个模块可以分别简化为一个倒立摆系统模型。双足机器人的倒立摆模型通常是将所有质量集中于质心，质心与零力矩点（ZMP）间由一个无质量的杆连接。ZMP处重力与惯性力所产生的合力矩在该点分量水平为零。对于双足机器人，ZMP的位置在双脚行走时在两脚之间来回移动，由于机器鼠身体较窄，可以忽略ZMP在垂直于前进方向上的移动，仅考虑前进方向上的力学特性[14]。

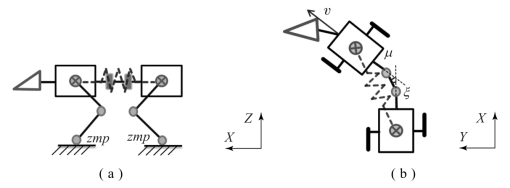
图5-36　足式机器鼠简化模型

（a）双倒立摆模型；（b）柔性腰部模型

机器鼠腰部由多连杆组成，其转动由两个舵机驱动，考虑哺乳类动物腰部类似弹簧特性的特点，在腰部有卷簧条件下可近似满足力学条件，因此机器鼠的腰部可简化为具有一个弹簧的柔性系统。在图5-36中，x2为机器鼠切向速度，φ为腰部和前半身的夹角。

通过上述简化模型，并对其进行动力学分析，得到机器鼠平面运动的状态方程为

式中，x1为前进方向下机器鼠质心的位移；x2为前进方向下机器鼠质心的速度；z为机器鼠质心高度；r为转弯半径；φ为腰部和前肢的夹角。

基于变量梯度法构建李雅普诺夫函数V（x）对此非线性系统进行稳定性分析。变量梯度法是1962年舒尔茨和吉布森提出针对非线性定常系统的稳定性判据。该方法通过设计相应的权重系数，得到满足稳定性要求（即的，然后对进行积分便可得到李雅普诺夫函数。通过对函数的正定检验，可以得到系统的稳定性条件[15]，构建其导函数式为(www.xing528.com)

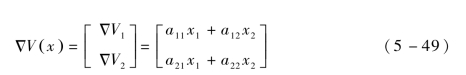
经过计算可得到当满足a12=a21＜0，a22=0，a11=a21·tanφ/r·x2时，V（x）的导数恒小于零，有

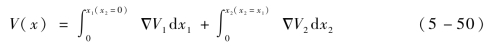
由式（5-48），将x1和x2代入式（5-50）化简得到，在机器鼠进行转弯时，有

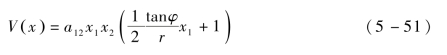
同理将式（5-48）改写成直线行走的状态方程，可得机器鼠直线行走时，有

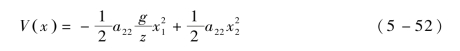
系统稳定的条件为对应的V（x）值大于零，该判据可以用来规划机身高度、步长、步频和腰部转角等信息。将机身高度、步长与步频等信息转换为机器鼠的质心高度及速度，将其与腰部转角同时代入，以分析能量函数是否满足大于零的条件。