轮式机器鼠的转弯运动分析与实验

轮式机器鼠由于具有多自由度的躯体机构，因此在仿生转弯方面具有较大的优势，可以实现与图2-20类似的转弯运动。因此，需要首先建立轮式机器鼠的简化模型。如图5-24所示，将机器鼠简化为具有M个关节的串联连杆机构以及一个位于机器鼠尾部的轮式行进机构。其中，连杆Li连接关节及，连杆的角位移为。特别地，标记机器鼠的鼻尖为，便于统一连杆的定义；同时，轮式行进机构的线速度定义为，机器鼠坐标系以及各连杆的质心如图5-24所示。

图5-24　轮式机器鼠简化模型

一、转弯模型

（一）运动学分析

将机器鼠的转弯路径抽象成为一个折线段AOB（图5-25（a）），当机器鼠的各关节点沿着该折线段运动时，机器鼠整体表现出来的就是一种转弯行为，至于相移过程，则体现在从L1到LM交替出现转弯行为上面。当转弯动作转移到Li时，和分别在AO和BO上，如图5-25（b）所示。此时，在已知关节角和关节沿AO的线速度的条件下，关节角速度和关节沿OB的线速度分别为

式中，Kr=tanαr；αr为转弯角。

因此，可以通过迭代的方式计算出机器人的关节角曲线和角速度曲线，从而控制机器鼠进行转弯行为。然而，上述计算关节运动变量的方法并不适用于车轮部的连杆LM，原因是LM是时刻垂直于两轮连线的，并且关节的转动不同于其他关节，只能通过两个轮子的差动运动来实现。因此，我们需要额外地对车轮部的转弯运动进行分析。图5-25（c）所示为车轮部的转弯模型。根据该模型，关节角度可以利用下式计算：

式中，B为两个车轮之间的宽度；dR和dL分别为左、右车轮的位移。

图5-25　转弯模型

（a）关节点路径；（b）单连杆转弯模型；（c）车轮部转弯模型

由于车轮部的特殊转弯方式，关节角度和也会在车轮部转弯时随之改变，并且它们可以表示为的函数，即

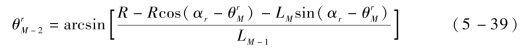
类似地，和的速度可以分别表示为

式中，。

（二）动力学分析

通过控制J1至JM-1以及最后一个链路中的两个车轮来实现机器人的转动动作，因此变量向量q可以表示为

因此，转动动作的动力学可以用下式中所示的拉格朗日函数表示，即

式中，；。

当机器人执行转动动作时，其势能U是常数，动能K随时间变化。Li的动能可以用ki表示，mi、Ii为Li的质量和惯量。

关于Li的质心的雅可比矩阵可表示为

其他雅可比矩阵具有与式（5-45）相似的形式。在该等式（5-45）中，XM，Gi、YM，Gi分别为从JM指向LGi的向量在X和Y方向上的投影长度。其余类似于XM，Gi和YM，Gi。

（三）N段转弯模型

由于关节角度范围的限制，机器鼠通常不能直接转过阈值角度αT。另外，机器鼠一次直接转过大角度就形态而言与实验鼠不相似。为了解决上述问题，可以使用N步转向策略（N≥2）。当机器鼠转过大于αT的角度时，转动角度被分成N个相等的部分（1～N），而且转动动作分别以N个单步骤实现。对于每个单步，运动学和动力学与上面讨论的相同，而关节角是N步计算值的总和。通过采用N步转动策略，机器鼠能够在转过大角度的同时执行转动动作，同时保持与实验鼠相似的仿生形态。

（四）转弯模型的仿真验证(www.xing528.com)

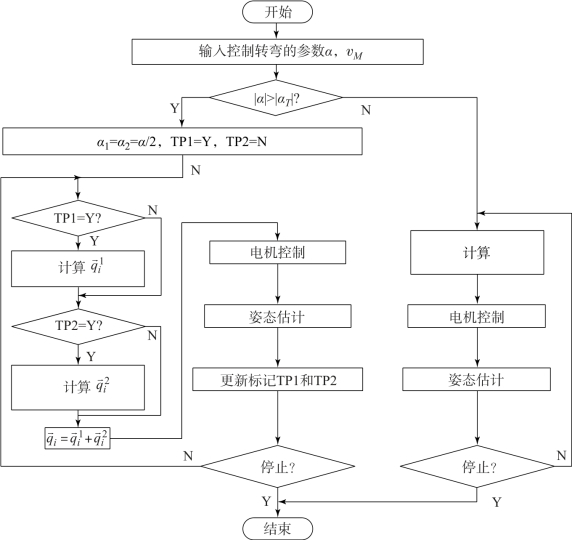
图5-26　转弯控制流程图

转动动作的控制流程如图5-26所示。开始时，应将转动角度和速度vM输入机器鼠，以便机器鼠知道转动方向（根据正、负号）、转动角度和速度。通过比较阈值角度αT，机器鼠决定直接转动或使用N步转向策略。

如果选择了N步转弯策略（如N=2），首先将TP1和TP2设置为标记两个转弯步骤的标志；然后机器鼠在单独的步骤中计算关节角度并将它们相加以控制机器鼠；最后进行机器鼠的姿势估计，并使用估计的姿势更新TP1和TP2标志，从而确定是否停止转动。

为了验证上述转动动作控制，在Matlab（Windows7，64位计算机中的Matlab 2018b）中进行仿真。在不失一般性的情况下，假设M、N两个车轮之间的宽度B和关节角阈值αT分别为64 mm以及45°。

（1）比较直接转弯动作和两步转弯动作。如图5-27（a）所示，机器人模型通过执行直接转动动作而转过30°。在整个转弯过程中，机器人只有一个链接随时执行转动动作，转动动作从第一个转换到最后一个，如图中的红波符号所示。然而，当机器人执行两步转动动作以转过60°时，机器人的两个连杆执行转动动作，除了转动过程的开始和结束，如图5-27（b）所示，对于每个转弯步骤，机器人仅转动30°。此外，可以在整个过程中找到相移。

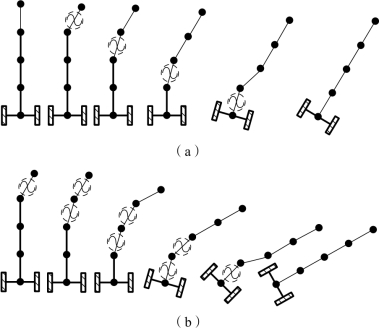
图5-27　转弯模拟示意图

（a）直接转弯；（b）两步转弯

（2）在直接转弯和两步转弯动作之间比较控制向量。如图5-28所示，图5-28（a）和（b）所示为用于直接转弯的控制向量；图5-28（c）和（d）所示为两步转动控制向量。对于两个车轮，在恒定和可变的vM下模拟了关节角度的变化。结果表明，两步转向在关节角度方面导致两个不同的峰值，并且所有峰值都低于阈值。显然，两步转向策略实现了关节角度限制下的大角度转向动作。此外，在这些图中可以清楚地发现相移过程，表明在机器人上实现了类似实验鼠的转动动作。

图5-28　关节角曲线与速度曲线

（a）恒定vM，直接转弯；（b）可变vM，直接转弯；（c）恒定vM，两步转弯；（d）可变vM，两步转弯

二、实验与评估

机器鼠WR-5M实现了直接和两步转动动作。转角设定为45°和90°。同样，符号表示转弯方向。根据αT的值，机器鼠可以决定采用直接转弯或两步转弯。两个转动动作的转动速度设定为25 mm/s。

图5-29显示了直接转弯和两步转弯的快照。当机器鼠进行直接转弯时，其平均转弯精度为45°，标准偏差为3.08°。对于两步转弯，平均转弯精度和标准偏差分别为94.2°和7.96°。为了直观地显示整个转弯过程，利用Kinovea在机器人转动时获得了每个关节的轨迹。Kinovea是免费但功能强大的运动视频播放器和分析软件，可以跟踪和测量运动[11]。分析结果显示在图5-30（a）和（c）中。数据显示，除了上的一些振动外，两种转向策略都实现了理想的转向动作。

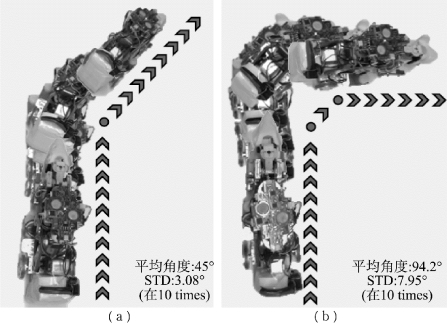
图5-29　机器鼠实验

（a）直接转弯；（b）两步转弯

在评估之前，首先记录了实验鼠的转弯动作并获得了其转向轨迹。为了更好地进行比较，使用和在鼻子、颈部、胸部和臀部标记了实验鼠，其分布与机器鼠WR-5M类似，如图5-31所示。然后，在Kinovea的帮助下获得了实验鼠转动动作的轨迹，如图5-30（b）和（d）所示。

可以发现，机器鼠和实验鼠具有类似的转弯轨迹，除了机器鼠的鼻端位置。机器鼠转动时会有一些不稳定。为了实现机器鼠与实验鼠转弯的相似性，我们进一步绘制转弯轨迹的轮廓并测量不同转弯阶段的宽度。

图5-30中的彩色背景是机器鼠或实验鼠转动时的包络线。使用不同转弯阶段的转弯轮廓宽度作为比较实验鼠和机器鼠的度量。S1、S2、S3分别表示机器鼠与实验鼠转弯前、转弯中和转弯后的不同阶段。为了消除形态引起的差异，进一步使用体长（BL）作为统一因子。在这种情况下，可以直接比较宽度来评估二者的相似之处。

实验鼠与机器鼠的比较结果如图5-32（a）和（b）所示。对于机器鼠WR-5M和实验鼠Rat，阶段S2中的转弯轮廓的宽度大于阶段S1和S3中的转弯轮廓的宽度。这意味着，实验鼠和机器鼠在转动时需要更多空间。该转弯空间为0.3～0.4 BL。此外，在所有阶段，机器鼠与实验鼠相比具有更小的转弯宽度，并且阶段S1和S3中的宽度比阶段S2中的宽度小得多。

图5-30　结果对比（见彩插）

（a）机器鼠直接转弯；（b）实验鼠直接转弯；（c）机器鼠两步转弯；（d）实验鼠两步转弯

图5-31　实验鼠标记点

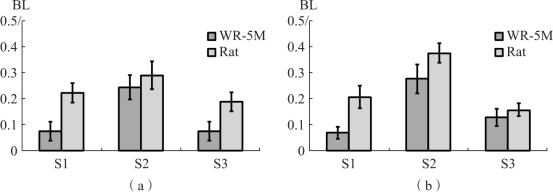
图5-32　机器鼠和实验鼠各转弯阶段的比较

（a）阶段S1；（b）阶段S2

综上所述，机器鼠以类似于实验鼠的方式进行转弯动作。在机器鼠上进行相移过程，其转动包络线小于实验鼠但与实验鼠相似[12]。