设计用于提取和识别实验鼠USV信号的混合声音信号处理系统

信号采集系统主要包括交互实验场地、上位机、相机和超声信号采集装置，如图4-25（a）中所示。为了在实验过程中记录实验鼠的发声和动作，将超声波麦克风和摄像头置于交互实验场地的顶部，麦克风采集到信号之后，会将信号传输到超声信号采集装置中（Avisoft UltraSoundGate 416Hb，图4-25（b））进行处理，最终输入上位机进行识别。USV采集装置最大的频率响应和采样率分别是140 kHz和300 kHz，完全覆盖了实验鼠USV的范围，满足实验要求，该装置的其他具体参数如图4-25（c）中所示。

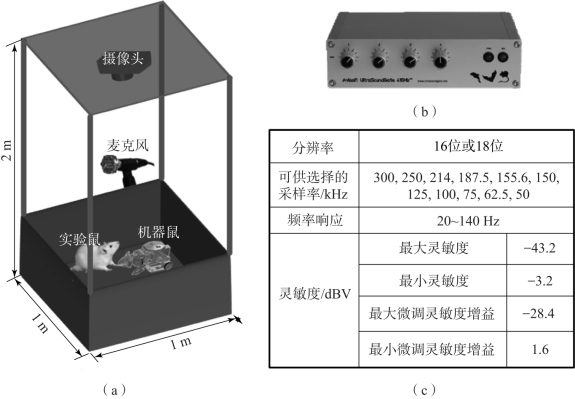
图4-25　听觉反馈系统搭建

（a）系统示意图；（b）超声信号采集设备Avisoft UltraSoundGate 416Hb；（c）信号采集系统的关键参数

一、实验鼠、机器鼠声音信号分析

设计听觉反馈系统需要考虑的关键问题是在混合有机器鼠噪声的声音信号中提取并识别实验鼠的USV信号。因此，有必要首先分析实验鼠、机器鼠和环境噪声的声谱图及其特点。因此，利用图4-25所示的系统分别单独记录了实验鼠和机器鼠在敞箱中运动的声音，并进行了分析。由于实验鼠的发声频率通常不会超过60 kHz，为了避免采样信号发生频域混叠，而且能够实现信号的实时处理，将超声信号采集装置的采样率设置为125 kHz。

在采集实验鼠声音时，我们选择10周龄的Long-Evans鼠作为实验对象，将实验鼠单独放入实验场地，使其自然地探索敞箱，记录实验鼠在探索周围环境的过程中的发声。尽管有许多方法可以刺激实验鼠发声，但是我们采用的方法可以最大程度避免记录到实验人员引入的环境噪声，从而更好地分析实验鼠发声的特点。实验鼠在实验期间是随机发声的，将实验记录到的声音数据修剪之后，计算出其时频谱图，如图4-26（a）所示。从图中可以看出，实验鼠的发声持续时间为30～50 ms，频率集中在40～60 kHz。此外，在20 kHz附近有持续的频率分量，这些分量来自环境噪声，这些噪声是计算机运行的噪声和动物房的通风设备的噪声等。

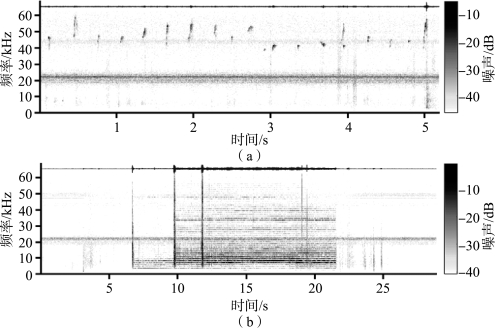
图4-26　实验数据的时频谱图（见彩插）

（a）实验鼠超声信号；（b）机器鼠运动噪声

机器鼠在交互实验中产生噪声的主要来源是机械装置之间的摩擦，以及各个关节的电机运动产生的噪声。图4-26（b）展示了机器鼠运动时产生的噪声的频谱，从7 s时开始到11.5 s时停止，机器鼠运动产生的噪声信号的频率成分是复杂且连续的，并且在大多数时候，机器鼠运动产生噪声信号的谐波延伸到了实验鼠发声的50 kHz附近。这些谐波的存在使我们不能通过直接检测40～60 kHz频率内是否存在明显的分量来判断实验鼠是否发声。此外，通过图4-26（b）可以发现，在10 s和12 s有两个明显的尖峰，这是由机器鼠的伺服电机快速运动引起的，这也会影响我们对实验鼠超声信号的检测。

二、SVM简介

支持向量机（SVM）是一种有监督学习模型[22]，计算复杂度与样本数量为线性关系，在数据量不大的场合下也可获得较高的分类精度。SVM的实现思路是对于给定的训练集样本D={（x1，y1），（x2，y2），…，（xm，ym）}，yi{+1，-1}，在样本空间找到一个划分超平面，将不同类别的样本分开。在样本空间中，超平面可通过如下线性方程描述：

式中，wT=（w1；w2；…；wd）为划分超平面的法向量，决定超平面的方向；b为偏移项，决定了超平面和原点之间的距离。

为了使超平面能将所有的训练样本正确划分，即对所有的训练样本，有下式成立，即

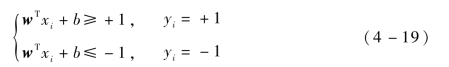
距离分类超平面最近的几个训练样本称为支持向量。其中，两个异类支持向量到超平面的距离之和称为“间隔”，即

SVM模型中的支持向量及支持向量之间的间隔如图4-27所示。

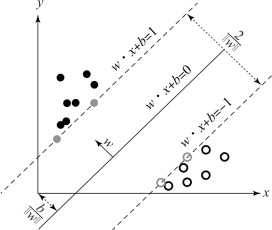
图4-27　支持向量与间隔

找到具有最大间隔的划分超平面，也就是要找到使γ最大化，并且能满足式（4-19）的参数w和b。为了方便计算，可将目标函数转化为‖w‖2最小。因此目标函数和约束函数为

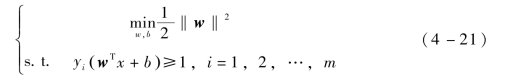
式（4-21）为SVM的基本型。SVM模型是一个不等式约束优化问题，求解SVM模型需要对式（4-21）引入拉格朗日乘子将其转换为对偶问题，可通过求解其对偶问题得到原问题的最优解。该问题的拉格朗日函数可写为

令L （w，b，α）对w和b的偏导数为零，可得

将式（4-23）和式（4-24）代入式（4-21）即可得到原问题的对偶问题：

由于原问题具有不等式约束，因此上述过程还需满足KKT（Karush-Kuhn-Tucker）条件：

由式（4-26）可知，这是一个二次规划问题，算法复杂度正比于训练样本数，在大数据情况下求解过程通常很慢，可以通过SMO（Sequential Minimal Optimization）算法高效求解。

当训练集并不是线性可分，即不存在能将训练集正确分开的分类超平面时，在实际应用中通常使用变换函数将原始训练集映射到更高维度的特征空间内。因为若原始样本是有限维的，则一定存在高维特征空间使得样本可分。

假设φ（x）是映射后的特征向量，将其代入式（4-21）中，可得新的目标函数和约束条件为

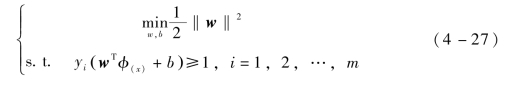
其对偶问题为

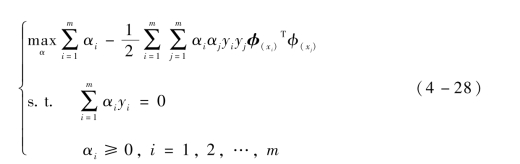
由于φ（x）的维度可能很大，此处为了便于计算，引入核函数的概念。现定义如式（4-29）这样的函数为核函数：(www.xing528.com)

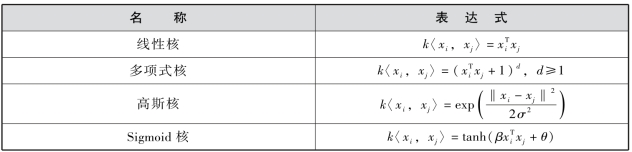
通过使用核函数，可以免于计算高维特征空间的内积，这极大地简化了计算过程。常用的核函数如表4-5所示。

表4-5　常用的核函数

三、预处理

由于在20 kHz附近的频段存在噪声，因此在信号处理之前应先对原始信号滤波，这里使用汉明窗高通滤波器对原始信号进行滤波处理，滤波器的幅频特性和脉冲响应如图4-28所示。滤波器的截止频率fcut为37.5 kHz，20 kHz附近的噪声可以被有效地抑制，而50 kHz附近的实验鼠超声信号几乎不受明显的影响。为了在截止频率的准确度与群延迟之间做出权衡，滤波器的阶数选择为128阶。在125 kHz采样率下，群延迟只有0.5 ms，几乎不会影响到信号的实时处理。

四、特征提取

通过SVM识别实验鼠50 kHz超声信号，可为后续机器鼠交互实验中判断实验鼠情绪状态，对机器鼠接近或远离实验鼠提供决策依据。基于SVM识别方法最重要的部分是需要选择合适的信号特征作为SVM分类器的输入变量，特征的选取会直接影响到泛化、计算复杂度和特征可解释性等诸多因素，并对分类精度有很大的影响。这里从时域、频域、能量域中选择了7个不同的特征进行分析。

（1）过零率（ZCR）。过零率是一种时域特征，描述了超声信号符号变化的比率，定义为

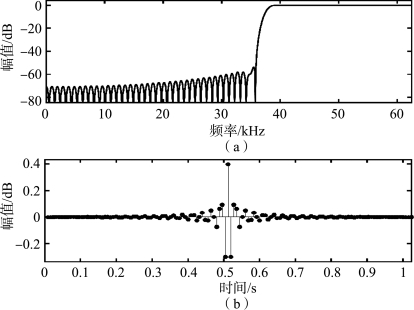
图4-28　截止频率为37.5 kHz的汉明窗128阶高通滤波器

（a）以分贝为单位的幅值响应；（b）脉冲响应

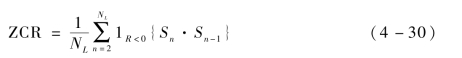
式中，Sn表示信号的第n个采样点；NL为声音块的长度；1R＜0{·}为指标函数，其含义为当{·}内的数值小于零时取值为1，其余情况下取值为零。

ZCR在区分超声信号与噪声方面有很好的效果，可以有效降低机器鼠运动的噪声掺杂对识别精度的影响，包含实验鼠超声信号的声音块往往具有很高的ZCR，而低频分量的ZCR数值往往非常小。

（2）能量熵（ENE）。能量熵是能量域的特征，反映了能量的分散程度。包含有实验鼠超声信号的声音块会具有很小的能量熵，而不含实验鼠超声信号的声音块会具有很大的能量熵。因此能量熵可以作为一个重要的特征去确定在包含机器鼠噪声的环境中是否存在实验鼠的超声信号。数据的滤波预处理也有助于使能量熵的区分效果更明显，因为滤波之后突出了原始信号的高频部分。将使实验鼠的超声信号有更大的能量熵变化，能量熵的定义为

其中，p（Sn）的定义为

（3）频谱形状特征。由于傅里叶变换不适用于分析非平稳随机信号，因此通过短时傅里叶变换（STFT）处理滤波后的超声信号，获取信号的频谱。超声信号在频域提供了更丰富的信息，因此选择了频谱质心（SCE）、频谱扩展（SSP）、频谱偏度（SSK）、频谱峰度（SKU）和频谱滚降（SRO）作为声音信号的频域特征，具体定义如下：

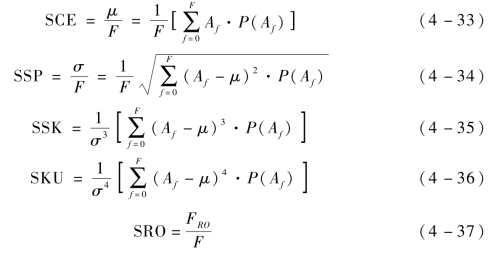
式中，Af表示信号频率为f时的幅频特性；F为奈奎斯特频率，数值等于采样率的。

P（Af）的定义为

FRO表示滚降频率，可通过下式计算：

这些频域特征描述了声音信号的频率分布，由于实验鼠的发声频率和机器鼠环境噪声有显著的区别，因此上述几个频域特征可以明显区分实验鼠超声信号。

最后，将上述所有特征整合为一个特征向量：

x=[ZCR,ENE,SCE,SSP,SSK,SKU,SRO]T

将输入向量和标签1用于训练SVM，用于特征识别。

五、SVM训练和识别

假设有Mr个包含实验鼠超声信号的训练样本以及Mnr个不包含实验鼠超声信号的训练样本，从这些训练样本中提取到的特征矩阵Xr和对应的标签向量为

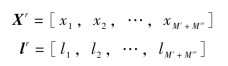
获取训练样本时，将实验鼠的超声信号与机器鼠运动产生的噪声混合作为训练样本，以最大限度地模拟交互实验时的真实情况。之后用长度为4 096个采样点的窗口修剪记录到的声音，并将声音块分为两类，即包含超声信号和不包含超声信号。该窗口的持续时间约为33 ms，具有与实验鼠超声信号相近的持续时间，且可以加速STFT过程的计算。

取总共Mr个包含实验鼠超声信号的样本和Mnr个不包含实验鼠超声信号的样本。在Matlab（R2018b）中训练SVM模型后，得到共mr+mnr个支持向量，其中mr个是关于包含实验鼠超声信号声音块的支持向量，mnr个是关于不包含实验鼠超声信号声音块的支持向量。训练完成后的支持向量矩阵记为Xs，权重向量记为pu，偏差记为ph，则

Xs、pu和ph共同确定用于SVM分类的超平面。当采集到一个新的声音块并得到它的特征向量x^时，可通过下式判断声音块中否包含实验鼠超声信号：

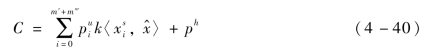
式中，k〈·〉为核函数，此处选择多项式核函数，即+1）2。