在仿生机器鼠与实验鼠进行交互过程中,需要仿生机器鼠对自身位姿进行估算,建立三维地图,以及计算机器鼠与实验鼠之间的距离,这些都需要事先获得图像点的空间信息。人类视觉是根据两只眼睛位置的不同,从而得到同一个物体从不同位置获得的图像,通过融合两张图像并根据图像中的差异来获取物体的深度信息。双目立体视觉作为机器视觉的重要组成部分,利用双目相机获取图像[5],由于存在视差,可以通过立体校正和立体匹配等方法建立两个图像特征点之间的对应关系,利用三角测量原理计算出像素之间的偏移来获取物体的三维坐标信息。
一、针孔相机模型
相机模型可以将三维世界中的坐标点通过投影映射到二维图像平面,这种相机模型种类很多,在此具体介绍的是其中最常见的针孔相机模型[6],如图4-6所示,其由光心O、光轴OO′和成像平面OX′Y′三部分构成。建立如图4-6所示的坐标系,并设三维空间的物体点P坐标为(x,y,z),光心O到OX′Y′平面的距离为f(即焦距),则有P经过光心O后投影在OX′Y′上的P′处,坐标为(x′,y′),根据相似三角形,可得
![]()
公式(4-1)中的负号(-)表示成倒立的像,数学上可以进行简化,将成像平面映射到相机的前方,即三维空间点与成像平面在相机坐标系的同侧,这样可以去掉负号使公式更加简洁,将式(4-1)整理后,可得
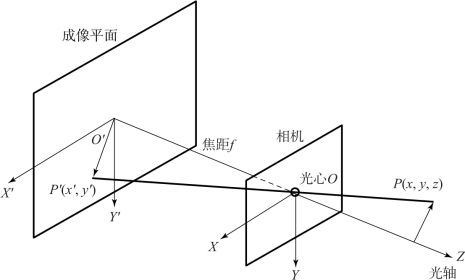
图4-6 针孔相机模型

这样便得到了空间中点在相机坐标系与成像平面坐标系之间的转换。不过,相机最终获得的是像素点,这就需要在成像平面上对像进行量化处理,涉及了坐标系之间的坐标转换。
二、相机坐标系转换
与相机相关的坐标系有世界坐标系、相机坐标系、成像平面坐标系和图像坐标系。这4种坐标系的定义及坐标转换的过程如图4-7所示。
世界坐标系Ow-XwYwZw满足右手法则,相机的位姿相对于世界坐标系由两个参数,即平移向量t和旋转矩阵R表示。相机坐标系Oc-XcYcZc以相机的光心Oc为原点,Zc轴沿着光轴方向指向相机前方,Xc轴水平向左,Yc轴竖直向下,且构成的相机平面与成像平面平行,OcOi为焦距长f。世界坐标系到相机坐标系的转换为刚体变换,对应关系以齐次坐标的形式表示如下:
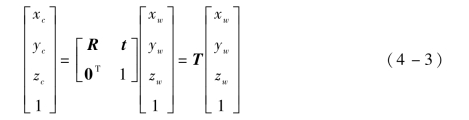
其中,R为一个3×3的旋转矩阵;t为三维平移向量;T为由R和t构成的4×4的齐次坐标变换矩阵。

图4-7 坐标转换示意图
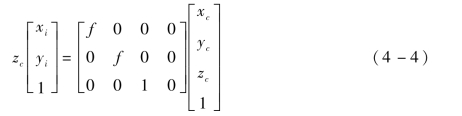
成像平面坐标系Oi-XiYi以成像平面的中心Oi为原点,Xi轴水平向左,Yi轴竖直向下。根据上述的小孔成像模型,可以得到相机坐标系到成像平面坐标系的齐次坐标转换公式为
图像坐标O-uv以图像的左上角O为原点,u轴与成像平面坐标系的Xi轴一致,v轴与成像平面坐标系的Yi轴一致。图像坐标系O-uv与成像平面坐标系Oi-XiYi之间,相差了两个缩放因子和一个原点的平移向量。假设图像坐标系在u轴上缩小了1/α,在v轴上缩小了1/β,同时原点平移了[cx,cy]T,那么成像平面坐标系与图像坐标系之间的齐次坐标转换公式为
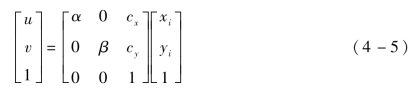
式中,α、β的单位为像素/mm,一般来说二者的值比较相近。
综合式(4-3)~式(4-5),可以推导得到图像像素坐标(u,v)和世界坐标(xw,yw,zw)之间的转换关系,即
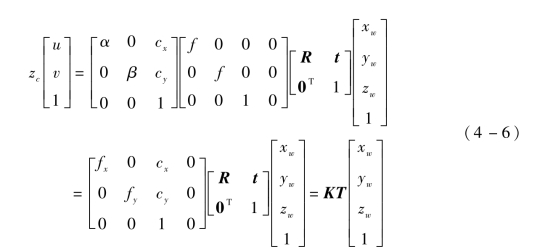
式中,fx=αf,fy=βf,分别为x、y方向上的等效焦距,单位为像素;矩阵K称为内参矩阵,由fx,fy,cx,cy决定,这4个参数仅与相机本身属性有关,一般在相机出厂之后是固定的;矩阵T称为外参矩阵,由平移向量t和旋转矩阵R决定。
三、双目测距原理
针孔相机模型描述了单个相机的成像原理,但是由于相机光心与图像平面某一点的连线上可以对应空间中无数点。因此,仅根据一个点在单个相机上的投影无法准确地获取具体的空间位置,也就无法恢复出物体的深度信息。为此,可以利用双目相机同步采集左、右相机的图像,进而匹配计算出视差,从而估计每个点的深度。双目相机的测距原理如图4-8所示。
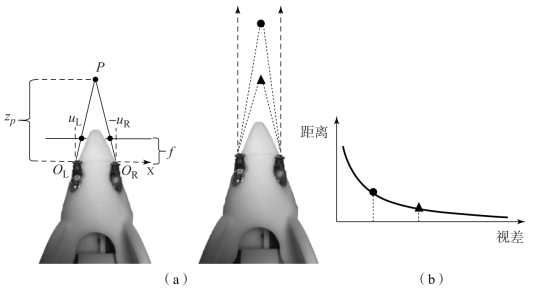
图4-8 双目测距原理
(a)双目测距示意图;(b)视差与距离的关系
图4-8(a)中左、右两个相机都可以看作针孔相机,并且水平放置。设两相机的焦距均为fc,它们的光心分别为OL和OR,而且相机坐标的x轴彼此重合,方向水平向右,OL与OR之间的距离为bLR,称为双目相机的基线。空间点P到相机原点的距离为zp(P点的深度),P点在左、右两个相机的成像平面各成一个图像PL和PR,由于两个相机位置不同,因此在两个相机下成像的位置有差异,理想情况下成像位置差只存在于水平方向上。设PL和PR在各自图像坐标系下的水平坐标分别为uL和uR,根据图4-8中相似三角形的关系,可得

整理式(4-7),可得

式中,dLR为左、右两张图像匹配点的横坐标之差(dLR=uL-uR),即视差,通过视差便可以计算空间中三维点的深度信息。
根据式(4-8)可以看出视差与距离成反比,如图4-8(b)所示,即距离双目相机越近的物体视差越大。另外,基线bLR越长,双目能测到的最大距离越远,而由于这是搭建的微型双目系统的基线很短,因此只能测量比较近的距离。为了保证实时性,选择的双目相机像素较低,所以在目标距离双目相机较远时会带来较大的测量误差。
如何准确计算目标在左右相机的成像对应关系是关键问题,主要原因是上述数学模型是建立在理想情况下的。但是,在实际应用中,由于安装误差等原因,双目视觉系统的左右相机并不是完全处在同一个平面上,相机光轴也并不完全平行,因此两个成像平面坐标系也存在着一定的平移和旋转。首先需要通过双目相机标定计算得到两个相机分别的内参和两个相机之间的外参;然后进行双目立体校正,使两个相机的图像每一行都对准,以便利用极线约束原理将匹配范围限制在每一行上。(https://www.xing528.com)
四、相机标定
双目相机的离线标定[7]主要是为了计算出两个相机的内参矩阵、外参矩阵和畸变系数,其中畸变系数是指由于透镜形状对光线传播的影响以及机械组装过程中的误差造成的图像边缘失真的现象。相机的畸变系数包括径向畸变系数k1、k2和k3,切向畸变系数p1和p2,以D=[k1,k2,k3,p1,p2]T表示。从总体来说,计算内参矩阵和畸变系数是为了得到相机固有性质并消除畸变,计算外参矩阵是为了得到两个相机间的位置与角度关系。相机标定的方法有很多,在此采用张正友标定法[8],并利用Matlab标定工具箱进行标定。标定的基本步骤如下。
(1)图像采集。双目相机同时各采集NC(NC通常取为20~25)张棋盘格图像,并保证每次拍摄时棋盘格处于不同位置和姿态。本书中用于标定的棋盘的方格大小为30 mm×30 mm。
(2)提取角点。Matlab标定工具箱会对每张图像都进行角点检测,角点检测结果如图4-9所示。

图4-9 角点检测结果
(a)左目相机;(b)右目相机
(3)参数获取。利用Matlab标定工具得到双目视觉系统的内参矩阵、外参矩阵和畸变系数。最终得到的标定参数如下。
左相机的内参矩阵为

左相机的畸变系数为
![]()
右相机的内参矩阵为

右相机的畸变系数为
![]()
左、右相机间的旋转矩阵

左、右相机间的平移向量为
t=[14.252-1.706 1.137]
五、立体校正
在完成相机标定之后需要进行立体校正,双目立体校正主要包括畸变校正和双目平行校正。畸变矫正是为了消除原始图像的畸变,还原图像的真实情况,提高匹配的准确性。畸变校正过程:首先,利用相机的内参矩阵将原始图像的图像坐标系变换到相机坐标系;然后,根据标定得到的畸变系数对图像的相机坐标进行校正;最后,利用内参矩阵将相机坐标系变换到图像坐标系,并将原始图像坐标的像素值赋值给新的图像坐标。
立体匹配寻找匹配点时要在图像的二维平面进行搜索,这样会导致匹配效率和准确性很低,这就需要进行双目平行校正。双目平行校正包括行校正和列校正:首先选择使用行校正,使得左、右两幅图像行对应;然后利用极线约束原理使得匹配搜索只需要在一维空间内进行。
极线约束过程如图4-10所示。OL和OR分别为左、右两相机的光心,现考虑空间一点P,在左、右两相机的成像平面IL和IR上成的像为PL和PR。点P、OL、OR三点形成的平面为对极平面,对极平面与两个成像平面IL和IR形成的交线lL和lR为极线。对于左极线lL上的成像点PL(QL),可能对应空间中的点P或者点Q,但不管对应哪个点,其在右相机成像平面IR的成像点必落在右极线lR上;反之,右极线lR上的成像点对应的匹配点也必然位于左极线lL上,这就是极线约束原理。
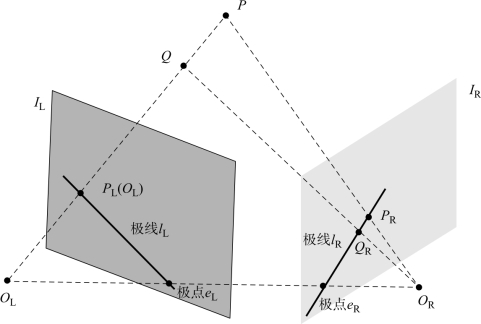
图4-10 极线约束
通过标定得到双目相机间的平移向量t和旋转矩阵R,可利用Bouguets算法[9]来最小化图像重投影畸变,从而完成双目平行校正。最终得到如下计算结果。
左相机校正后的旋转变换矩阵为

右相机校正后的旋转变换矩阵为

双目立体校正前后对比如图4-11所示。由图可以看出,校正后的双目图像消除了畸变并使得左、右相机图像中的对应像素点在同一行上,将匹配从二维空间降低到一维空间,从而提高双目立体匹配的速度与准确度。

图4-11 双目立体校正
(a)双目立体校正前;(b)双目立体校正后
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




