如何计算非完全平方数二次根式？

在数控加工中，经常要对图样上的一些数据做处理，三角函数、极坐标、勾股定理等是经常用到的，很多时候，不可避免地要和二次根式打交道。在手头没有科学型计算器的情况下，有没有一种简便可行的方法能快速且准确地计算出能满足机床运行精度的数值呢？

笔者结合平方根式和完全平方公式，推导出一种简便的计算二次根式的方法，使用起来得心应手，奉献出来，以飨读者。

如果采用逆向思维，可以把二次根式看作是完全平方公式的逆运算，已知完全平方公式为：（a±b）2=a²±2ab＋b²。如果a＞＞b＞0，且b的值很小，则b²趋近于0，可以忽略，则公式蜕变为：（a±b）2≈a²±2ab，则。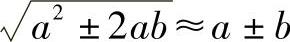

例1：求？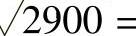

已知54²=2916，接近于被开方数2900。令a=54，则2ab=（2900－2916），求得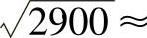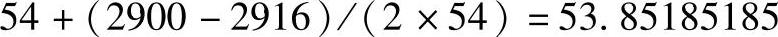，和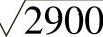的值53.85164807相差2.0378×10^－4，满足机床分辨率要求。

例2：求？

①已知58²=3364，接近于被开方数3375。令a=58，则2ab=（3375－3364），求得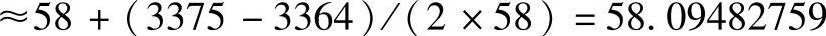，和的值58.09475019相差7.7393×10^－5，满足机床分辨率要求。(www.xing528.com)

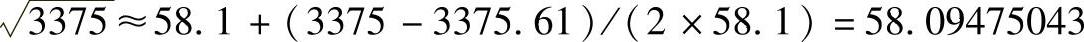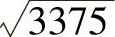②若更进一步，已知58.1²=3375.61，更接近于被开方数3375。令a=58.1，则2ab=（3375－3375.61），求得，和的值58.09475019相差2.3718×10^－7，满足机床分辨率要求。

例3：求？

已知68²=4624，69²=4761，显然69²更接近于被开方数4712。令a=69，则2ab=（4712－4761），求得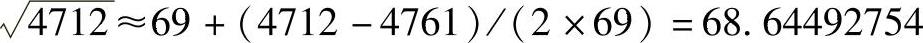，和的值68.64400921相差9.1833×10^－4，满足机床分辨率要求。

例4：求=？已知57²=3249，接近于被开方数3272。令a=57，则2ab=（3272－3249），求得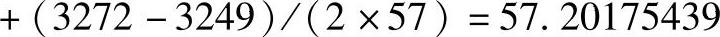，和的值57.20139858相差3.5580×10^－4，满足机床分辨率要求。

为了更快地计算出大约数，对式中的除法可以快速估算商值，例如61÷58.1=？商为1后余数为2.9，如果把除数看成是58，则61÷58.1≈1.05，和真实值1.0499139相差很小；有时可以利用差值法快速计算大约数，例如230÷49=？若令除数为50，商为4.6，49和50相差1/49，把商值加上其1/49即可，为了快速计算，可以取1/50，所以大约数为4.692，和真实值4.6938776相差很小。