矩形周边外斜面的球头铣刀加工优化策略

如图5-18所示，有一矩形工件，其坐标系零点设置在对称中心上，上表面为Z＃7，左右斜面与垂直面的夹角为＃3，前后斜面与垂直面的夹角为＃4，在这里规定＃3=＃4。

如果＃3≠＃4，虽然两组斜面的相交线在任意深度对应的X、Y坐标容易求出来，但由于刀具移动到的Z坐标和这两个角度相关，若＃3≠＃4，在连续加工中，不便描述其轨迹。如果加工完一组相对的斜面后，再加工另一组相对的斜面；或加工完某一侧的斜面后，延长一段距离，再加工一相交的斜面，也可以编写出程序，只是有空行程。

下刀点可以选择在工件的任一角上，如铣削深度相对球头铣刀半径的比例较小，建议从下而上逐层铣削，进给以顺铣方式。

在使用球头铣刀的斜面加工中，确定球头铣刀刀尖在初始刀位点的Z坐标值需要烦琐的计算。

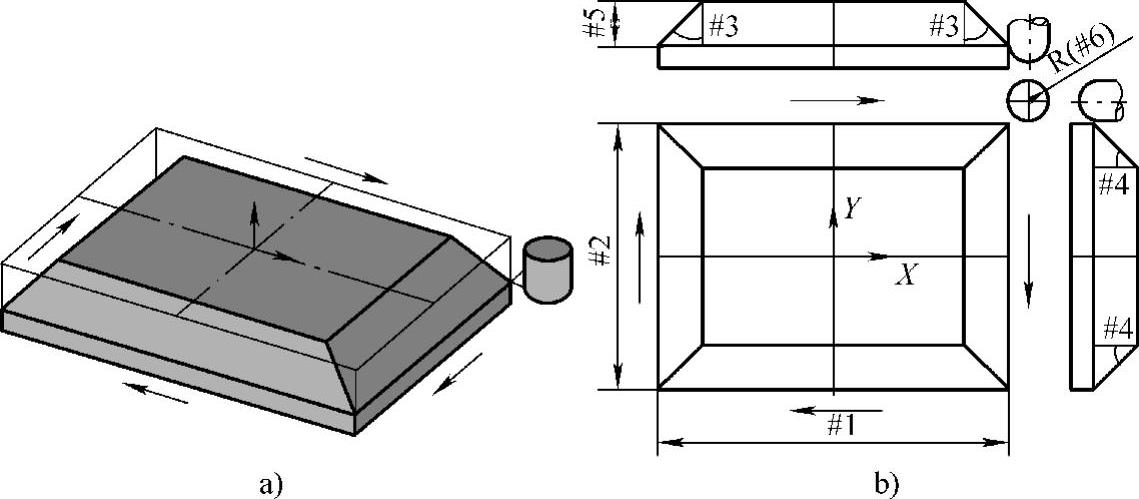
图5-18 矩形周边外斜面（球头铣刀）加工示意图

如图5-19所示，已知球头铣刀半径r，斜面与垂直面的夹角α，斜面高度h，求初始加工时铣刀刀尖的Z坐标值Z_A，加工斜面时刀心（刀具）在Z轴的移动距离KM。

推导过程如下：

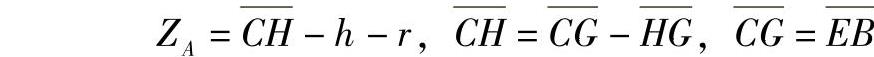
在△ABE中

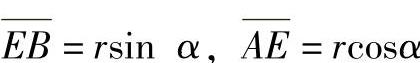
在△BGH中

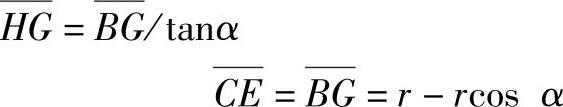
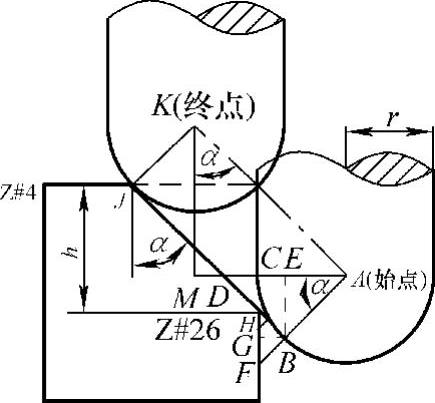
图5-19 球头铣刀加工斜面的数学计算

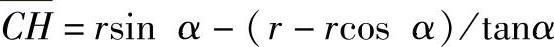
根据三角函数关系代换，化简得

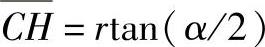
则自下而上初始加工时球头铣刀刀尖相对于斜面最高点J的坐标值为

Z_A=rtan（α/2）－h－r

在△AKM中

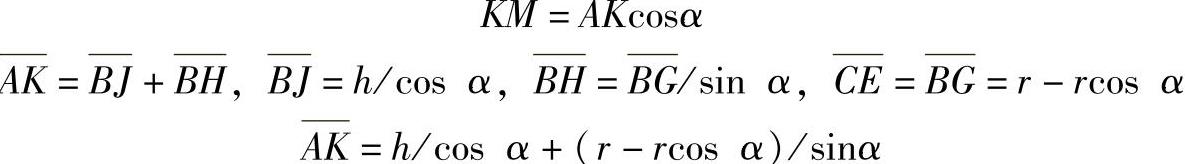(www.xing528.com)

故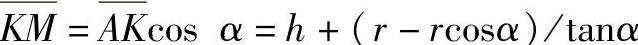

根据三角函数关系代换，也可以表示为

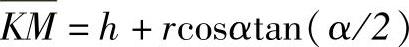
各变量赋值说明：

＃1=A，矩形X向的边长。

＃2=B，矩形Y向的边长。

＃3=C，周边斜面与垂直面的夹角α。

＃4=I，斜面最高点J的Z轴绝对/相对坐标值。

＃5=J，球头铣刀半径值。

＃17=Q，等高铣削每次的递增量，＞0。

＃24、＃25=X、Y，矩形对称中心X、Y的绝对/相对坐标值。

＃26=Z，斜面最低点H的Z轴绝对/相对坐标值。

调用格式：

G65 P1070 A_B_C_I_J_Q_X_Y_Z_F_；

宏程序如下：

说明：

①若是平行四边形周边斜面加工，周边斜面与垂直面的夹角α相等，也可以结合上述两个程序加工。

②如需粗精加工，可以先用平底立铣刀加工平行四边形周边斜面的程序粗加工，再用这个程序精加工。