平行四边形周边外斜面的优化加工方法

如图5-17a、b所示，有一平行四边形工件，其左下角的点在工件坐标系中的坐标值为（X，Y），左右斜面的斜度相等，前后斜面的斜度相等，这两对斜度可以不相等。采用顺铣方式加工，下刀点在左下角的A点，若铣削深度与刀具直径的比例值较小，刚性较好，可以从下向上逐层加工；若比例值较大，可以从上向下逐层加工。本例为从下向上加工。

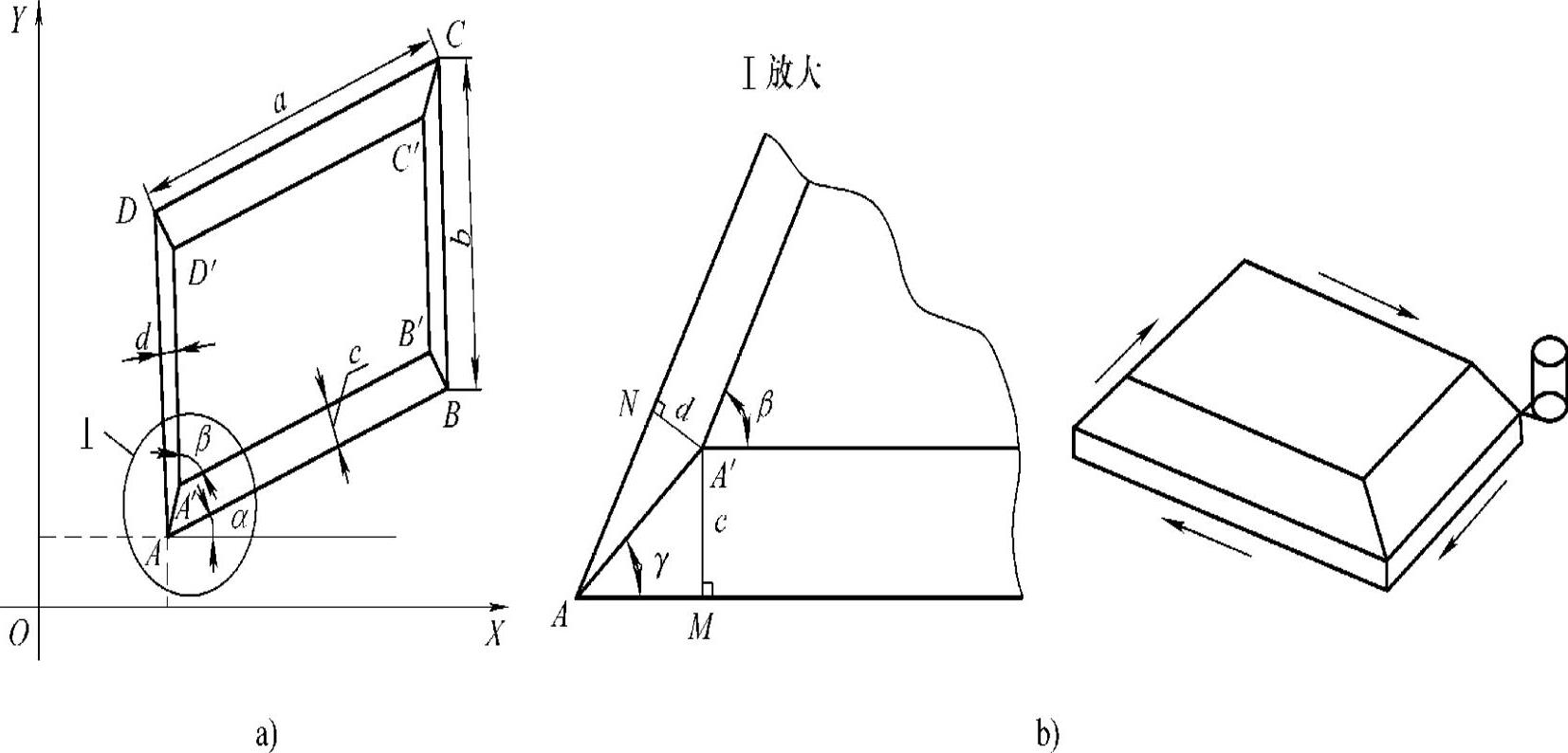
图5-17 平行四边形周边外斜面加工示意图

如果把三维的看作是二维的，问题的解答就方便多了。

其实这道题在XY平面的投影图和一道关于焊接的题类似：厚度相同，宽度分别为c和d的两块钢板需焊接在一起，焊接后所成角度为β和180°－β，问两块钢板分别应如何切割角度？

如图5-17a、b所示，在平行四边形ABCD中，若∠DAB=∠BCD=β，则∠CBA=∠ADC=180°－β。设宽度为c的钢板应切割的角度∠A′AB=γ，经过点A′作AB的垂线，垂足为M，经过点A′作AD的垂线，垂足为N，则在△A′AM和△A′AN中，有

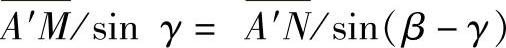
即 c/sinγ=d/sin（β－γ）

根据和差角公式，解得

γ=arc tan［csinβ/（d＋ccosβ）］

同理，解得

γ′=∠ABB′=∠CDD′=arc tan［csinβ/（d－ccosβ）］

那么另一块宽度为d的钢板的切割角度分别为β－γ和180°－β－γ′。

由于0°＜β＜180°，所以sinβ＞0，而（d＋ccosβ）或（d－ccosβ），其值大于、小于或等于0的情况都存在，所以根据分子分母所在的位置，通过反正切函数求得的角度值为0°＜γ＜180°，恰好符合题意。由于在除法算式中分母不能为0，所以用反正切函数时要考虑到，当分母为0时，角度就是90°，即当（d＋c cosβ）或（d－ccosβ）值为0时，相对应的角度为90°。

可即便求出了γ，想计算A′A上任意有效Z坐标值所对应的X坐标值仍然要用正切函数tanγ，而γ=90°仍然是道门槛，因sin 90°有值，倒不如通过c/sinγ求出A′A的长度，再用这段长度γ求得A′A上任意有效Z坐标值所对应的点到A点的距离，Y轴距离为＃3∗＃18，根据实际情况判断正负符号。

由于刀具中心始终与任意深度对应的平行四边形的4条边的延长线相距一个刀具半径，所以刀具中心一定在任意深度对应的平行四边形顶角平分线的反向延长线上。即，在以A点为旋转中心，旋转了－α的坐标系中，刀心到另一顶点的X轴距离为0.5∗＃7/TAN［＃6/2］；或0.5∗＃7/TAN［90－＃6/2］，即0.5∗＃7∗TAN［＃6/2］，为程序中的＃12、＃15；Y轴则始终相差一个刀具半径，0.5∗＃7。

在以A点为旋转中心，旋转了－α的坐标系中，平行四边形ABCD各顶点的坐标为A（0，0）、B（a，0）、C（a＋bcosβ，bsinβ）、D（bcosβ，bsinβ）。

各变量赋值说明：

＃1=A，平行四边形ABCD中AB、CD的边长a。

＃2=B，平行四边形ABCD中BC、DA的边长b。

＃3=C，AB和A′B′、CD和C′D′在XY平面上的投影线之间的距离。(www.xing528.com)

＃4=I，BC和B′C′、DA和D′A′在XY平面上的投影线之间的距离。

＃5=J，平行四边形ABCD中AB和＋X轴之间的夹角α。

＃6=K，平行四边形ABCD中∠DAB、∠BCD的角度β，0°＜K＜180°。

＃7=D，平底立铣刀直径。

＃8=E，平行四边形A′B′C′D′的Z轴绝对/相对坐标值。

＃17=Q，等高铣削每次的递增量，＞0。

＃24、＃25=X、Y，平行四边形ABCD中A点的绝对/相对坐标值。

＃26=Z，平行四边形ABCD的Z轴绝对/相对坐标值。

调用格式：

G65 P1060 A_B_C_I_J_K_D_E_Q_X_Y_Z_F_；

宏程序如下：

说明：

①N10～N70、N70～N100，计算∠A′AB、∠B′BA，由于角度为90°时正切函数无意义，所以采用了这种特殊的计算方法。

②在WHILE循环中，下面有横线的依次为A、D、C、B、A的坐标，下面有点■的依次是Z＃16平面与A′A、D′D、C′C、B′B、A′A的交点的坐标，下面有锯■齿■■线的是刀具中心相对于该交点的坐标。

③在0°＜β＜180°范围内，一般情况下，β或（180°－β）的取值不会过大或过小；若过大或过小，则刀具中心相对于Z＃16平面与A′A、B′B、C′C、D′D的交点的X轴距离0.5∗＃7/tan（β/2）或0.5∗＃7∗tan（β/2）必然很大，如果临近有凸台或工件，请注意，以免发生碰撞！

④若需从上向下加工，需对程序做一下修改。

⑤若需粗精加工，可以调用两次该宏程序，粗加工时把＃7设置得比实际值大一些，精加工时如实设置。