长期以来,网络上和一些书籍里在椭圆的认知上都存在一个很大的误区:认为只要刀具中心的移动轨迹是椭圆,加工出来的内/外轮廓也必然是椭圆,这一点对于圆来说毫无疑问是正确的,但对于椭圆来说则未必如此。由这个错误的认知而编写的椭圆宏程序也必然是错误的。可以来验证一下。
如图5-9所示,中间的实线所示的椭圆轮廓,在X轴上的半轴长度a=50mm,在Y轴上的半轴长度b=40mm。若按照这种说法,内层的虚线所示为内轮廓铣削时刀具中心的椭圆轨迹,在X轴上的半轴长度a=40mm,在Y轴上的半轴长度b=30mm;外层的虚线所示为外轮廓铣削时刀具中心的椭圆轨迹,在X轴上的半轴长度a=60mm,在Y轴上的半轴长度b=50mm;恰如用ϕ20mm的刀具来加工实线椭圆所对应的内、外轮廓时刀具中心的移动轨迹一样。
很多人在以角度作为步距值编写椭圆宏程序的时候,往往不小心就进入了一个误区,把椭圆上的某点所对的中心角α混淆为该点所对的离心角θ,导致编程错误。
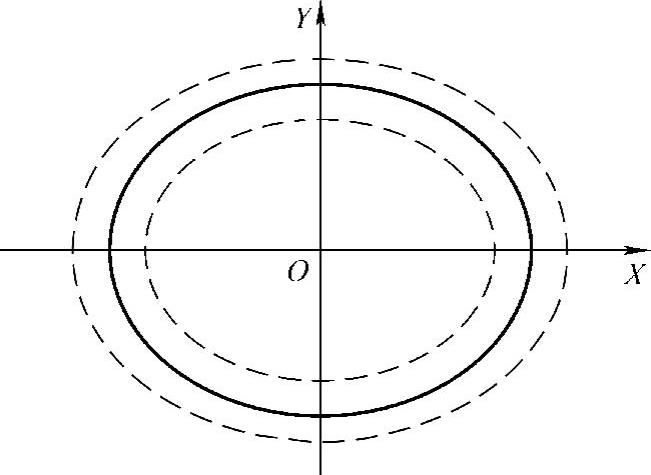
图5-9 椭圆及其内、外轮廓
椭圆上的离心角θ和中心角α如图5-10所示。
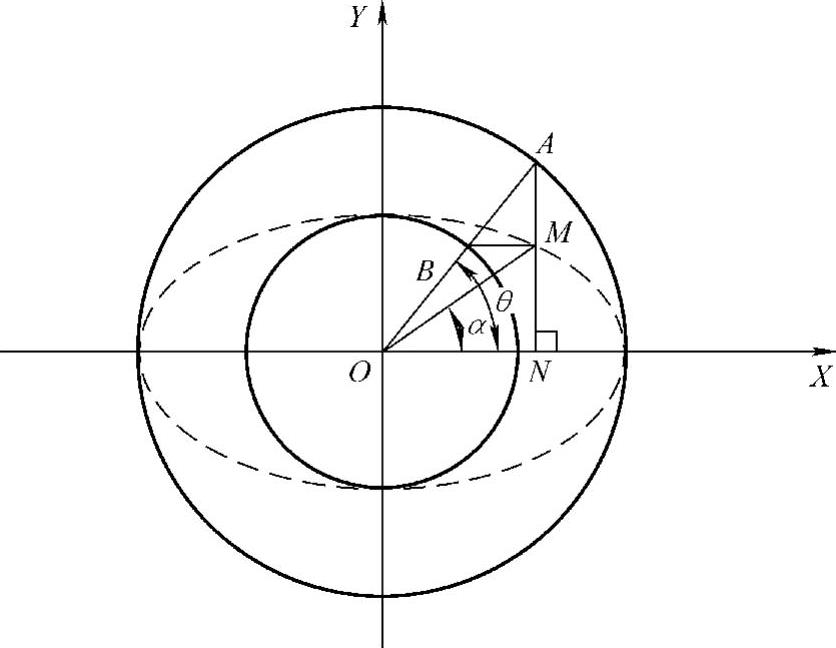
图5-10 椭圆上的离心角θ和中心角α
图中,经椭圆中心O作两个圆,半径分别是椭圆长半轴长度a和短半轴长度b,经椭圆上的任意一点M作X轴的垂线交X轴的垂足为N,反向延长后交半径为椭圆长半轴长度a的大圆于A点,连接OA,交半径为椭圆短半轴长度b的小圆于B点,连接BM,∠AMB=90°,则有
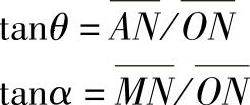
由于△ABM∽△AON,所以MN/AN=BO/AO=b/a。
所以,推出:tanθ=atanα/b(离心角θ和中心角α在同一象限,α≠90°、≠270°)。
设经过椭圆中心的直线与平面第一轴正方向(+X)的夹角为α,即椭圆上的点对应的中心角α,根据椭圆标准方程和直线方程的联立,求解。
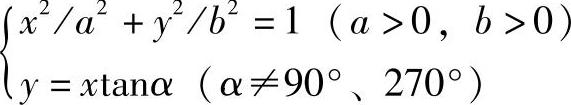
解得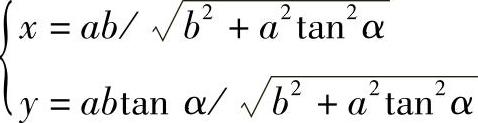
根据三角函数关系代换,也可以变形为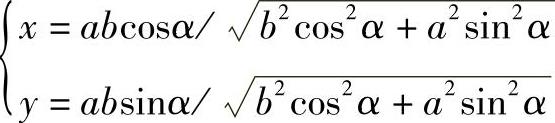 。两点之间的距离d=
。两点之间的距离d=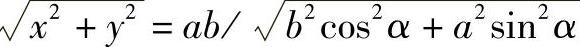 。
。
为了证明这是一个伪命题,只需找出某一个角度在图5-9中3个椭圆上所对应的3个点每相邻两点之间的距离不相等,也不等于刀具半径10mm就行了。如果用同一个离心角θ,会发现相邻两点之间的距离都是10mm,而离心角θ和椭圆的离心率有关,并不代表该点真实的角度;所以只能用中心角α,角度要满足一个条件:不等于0°、90°、180°或270°。
限制中心角α不等于90°、270°,并非因为这两个角度不适用于以中心角α为参数的椭圆方程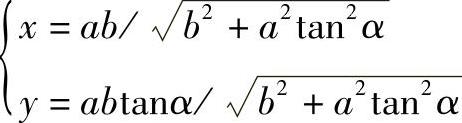 ,也非因为这两个角度适用于其变形方程
,也非因为这两个角度适用于其变形方程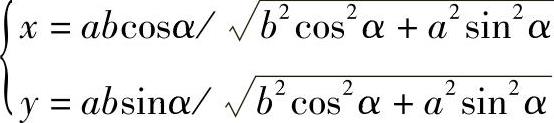 ,而是,在这4个特殊角度下,反映在3个椭圆上所对应的3个点每相邻两点之间的距离相等,正是刀具半径10mm,而这一点恰恰是被许多操作者重视的。通常,检查椭圆是否合格,都是去测量其长轴和短轴的长度,认为只要这两处尺寸对了,轮廓就是椭圆了,而这两个尺寸正好合乎图样的标注,导致错误不易被发现。虽然错误阴差阳错地被忽略了,但错误毕竟还是错误,利用数学计算来指导实践,通过测量是能发现的。
,而是,在这4个特殊角度下,反映在3个椭圆上所对应的3个点每相邻两点之间的距离相等,正是刀具半径10mm,而这一点恰恰是被许多操作者重视的。通常,检查椭圆是否合格,都是去测量其长轴和短轴的长度,认为只要这两处尺寸对了,轮廓就是椭圆了,而这两个尺寸正好合乎图样的标注,导致错误不易被发现。虽然错误阴差阳错地被忽略了,但错误毕竟还是错误,利用数学计算来指导实践,通过测量是能发现的。
①当椭圆中心角α=50°,由方程可以计算出,该角度交内层椭圆的点的坐标为(21.305138,25.390475),交中间椭圆的点的坐标为(27.867450,33.211133),交外层椭圆的点的坐标为(34.382976,40.976035),可以计算出内层、中间椭圆上的两点间的距离为10.209144mm,中间、外层椭圆上的两点间的距离为10.136359mm,而10.209144≠10.136359≠10。②换言之,椭圆中心角α=50°时,交3个椭圆上的点到椭圆对称中心的距离
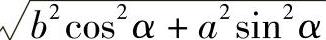 ,椭圆对称中心到内层、中间、外层椭圆的距离计算结果依次为:33.1449mm、43.3541mm、53.4904mm。也即,若用游标卡尺从α=50°和α=230°来测量中间的椭圆,尺寸应该为2×43.354mm≈86.70mm;但现在,若为内轮廓铣削,测量的尺寸为(2×33.145+20)mm≈86.30mm;若为外轮廓加工,测量的尺寸为(2×53.490-20)mm≈86.98mm。而86.30≠86.70≠86.98,相差这么多,用游标卡尺就能测量出来!若能把这么大的错误理解成误差,机床怕是早该维修了。但问题的关键是,又有谁会从相差180°的50°和230°的位置去测量这个椭圆呢?或许压根就没想到这么多。其实,机床已经按照编程者的程序真实地记录下了这个错误,只不过许多人过于想当然地认为,对错误视而不见罢了。
,椭圆对称中心到内层、中间、外层椭圆的距离计算结果依次为:33.1449mm、43.3541mm、53.4904mm。也即,若用游标卡尺从α=50°和α=230°来测量中间的椭圆,尺寸应该为2×43.354mm≈86.70mm;但现在,若为内轮廓铣削,测量的尺寸为(2×33.145+20)mm≈86.30mm;若为外轮廓加工,测量的尺寸为(2×53.490-20)mm≈86.98mm。而86.30≠86.70≠86.98,相差这么多,用游标卡尺就能测量出来!若能把这么大的错误理解成误差,机床怕是早该维修了。但问题的关键是,又有谁会从相差180°的50°和230°的位置去测量这个椭圆呢?或许压根就没想到这么多。其实,机床已经按照编程者的程序真实地记录下了这个错误,只不过许多人过于想当然地认为,对错误视而不见罢了。
所以要想铣出椭圆内、外轮廓,刀具中心的移动轨迹就必然不是椭圆,而是其偏移曲线。在加工时,必须要用刀具半径补偿。
对椭圆方程x2/a2+y2/b2=1(a>0,b>0)及其偏移方程,加工其内轮廓,对刀具半径值有限制,椭圆内轮廓上的各点,在其长轴处两点的曲率半径最小,为短半轴2/长半轴。若用刀具加工该处,要满足R刀≤短半轴2/长半轴,或者说,d刀≤短轴2/长轴;加工椭圆外轮廓,对刀具半径值无限制。
对抛物线方程y2=2px(p≠0),或x2=2py(p≠0)及其一般方程,加工内轮廓,在其顶点处开口内侧的曲率半径最小,为∣p∣。若用刀具加工该处,要满足R刀≤∣p∣,或者说,d刀≤2∣p∣;加工抛物线外轮廓,对刀具半径值无限制。
对双曲线方程x2/a2-y2/b2=1(a>0,b>0),或y2/b2-x2/a2=1(a>0,b>0)及其偏移方程,加工内轮廓,在其上、下、左、右半支顶点处开口内侧的曲率半径最小,为虚半轴2/实半轴。若用刀具加工该处,要满足R刀≤虚半轴2/实半轴,或者说,d刀≤虚轴2/实轴;加工双曲线上、下、左、右半支外轮廓,对刀具半径值无限制。
1.椭圆内轮廓加工
内轮廓的加工分为两种情况,椭圆内轮廓的内部是空的或是有其他结构,应根据不同的情况,选取不同的进给路径,如图5-11所示。
各变量赋值说明:
#1=A,椭圆长半轴长度a,>0。
#2=B,椭圆短半轴长度b,>0。
#3=C,椭圆内轮廓上表面Z轴的相对/绝对坐标值。
#4=I,椭圆铣削时角度自变量#6每次的递增量,>0。(https://www.xing528.com)
#7=D,刀具直径,>0。
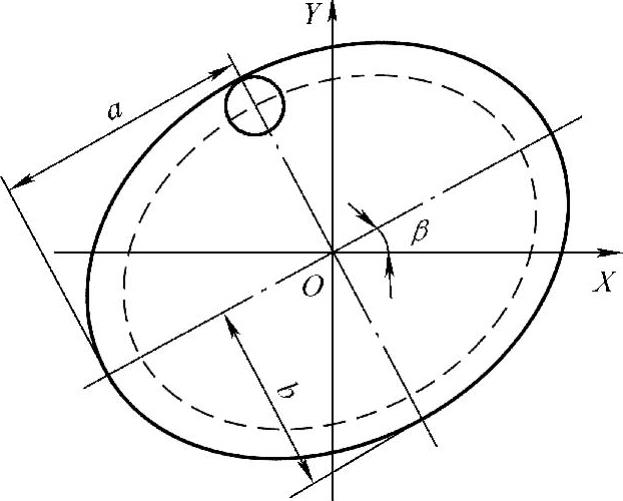
图5-11 椭圆内轮廓加工示意图
#17=Q,深度铣削每层下降的深度,>0。
#18=R,椭圆长轴与+X轴的夹角。
#24、#25,椭圆中心X、Y轴的相对/绝对坐标值。
#26,椭圆内轮廓底面Z轴的相对/绝对坐标值。
调用格式:
G65 P1088 A_B_C_I_D_F_Q_R_X_Y_Z_;
1)椭圆轮廓内部有其他结构时的宏程序:


2)椭圆轮廓内部无其他结构时的宏程序:


说明:
①对以上两个宏程序中的程序段N6~N9、N30、N31的描述,均为参数No.6000#3=1时的情形。
②以上两个宏程序中的程序段N8、N9,也可以编写为:
G90 G10 L12 P1 R[#7/2];
G90 G10 L13 P1 R0;
2.椭圆外轮廓加工
如图5-12所示。
虽然刀具直径在椭圆的外轮廓加工时没有限制,但仍可能受限于其他因素。
各变量含义和调用格式同上。
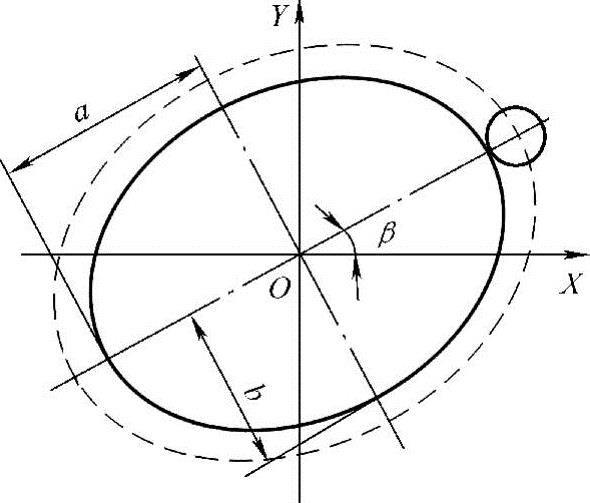
图5-12 椭圆外轮廓加工示意图



免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




