图3-10所示的便是由三通阀组成的动力机构。为了使活塞能够反向运动必须使用两腔面积不等的液压缸。本节将分别讨论零重叠三通阀及负重叠三通阀的综合特性方程及其有关阀系数。
1.零重叠三通阀
三通阀在机-液位置伺服系统中得到了最广泛的应用,而且总是优选零重叠的三通阀,因此就更有必要研究其综合特性了。
在图3-10中,若令Δ=0,便成了由零重叠三通阀组成的动力机构。其负载流量方程为
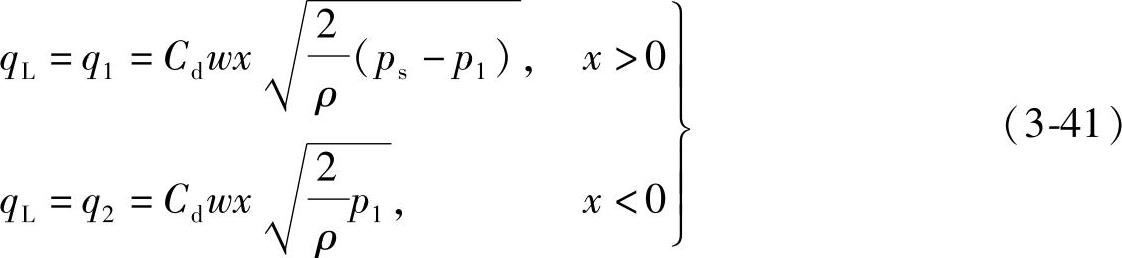
为了画出其综合特性曲线,也可仿照四通阀那样将式(3-41)化成无因次形式
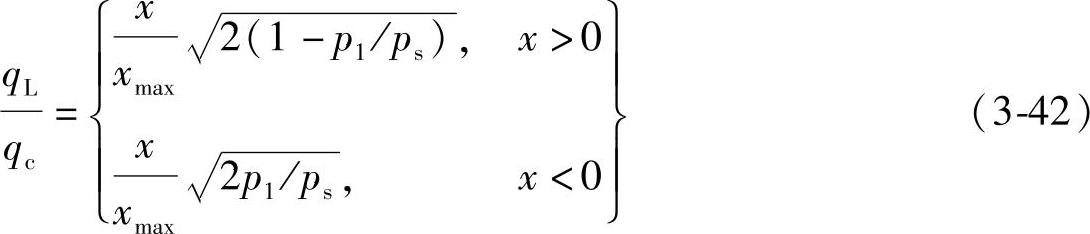
若仍以x/xmax为参变量,以qL/qc为纵坐标,以p1/ps为横坐标,则可画出零重叠三通阀的负载压力-流量曲线(综合特性曲线),如图3-20所示。将图3-20与图3-16对比发现两者的曲线形状完全一样,只是横坐标“-1”点变成了“0”点。
三通阀的线性化增量方程可由式(3-41)得出
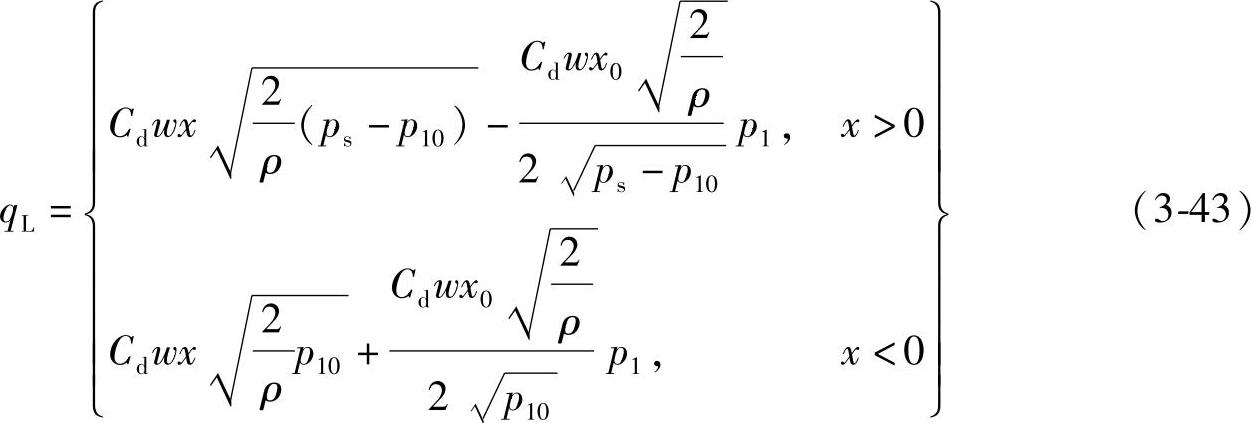
由式(3-43)看出,一般情况下,x>0和x<0时的流量增益和流量-压力系数是不相等的,此点从图3-20也可看出。三通阀控制系统的工作点若选在零位,液压缸活塞在两个方向上的运动状态就不连续。为了克服这一点,可选择工作点处的p10满足下式

因此式(3-43)又可写成式(3-27)的形式,即
qL=kxx-kpp1
式中
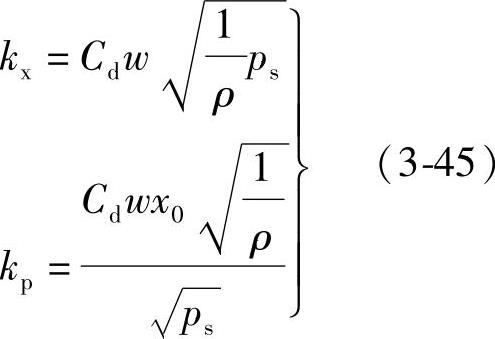
由此得到
kpx=ps/x0(3-46)
显然,此时三通阀在工作点处两个方向上的特性便连续了。为了满足式(3-44),当液压缸活塞没有弹性负载及常值外干扰力时,两腔活塞有效面积之比应满足式(3-47)
A1=2A2(3-47)如果有常值外干扰力,仍可通过A1与A2之比来满足式(3-44)。
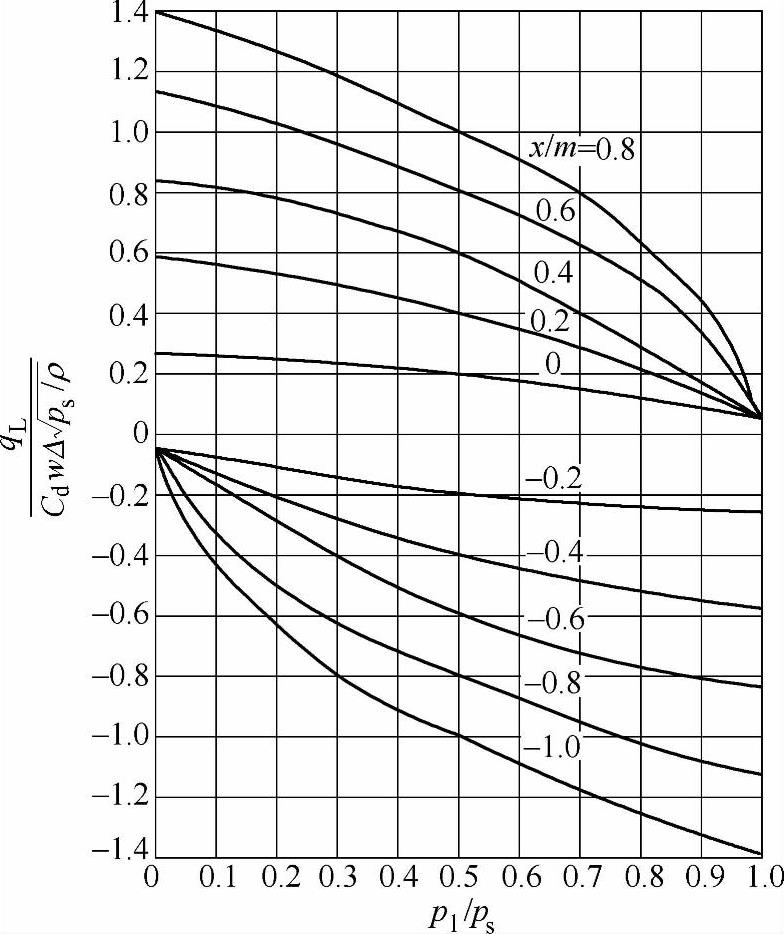
图3-20 零重叠三通阀的负载压力-流量曲线
若将零重叠四通阀的工作点的负载压力选为pL0=0,则由式(3-37)可得到
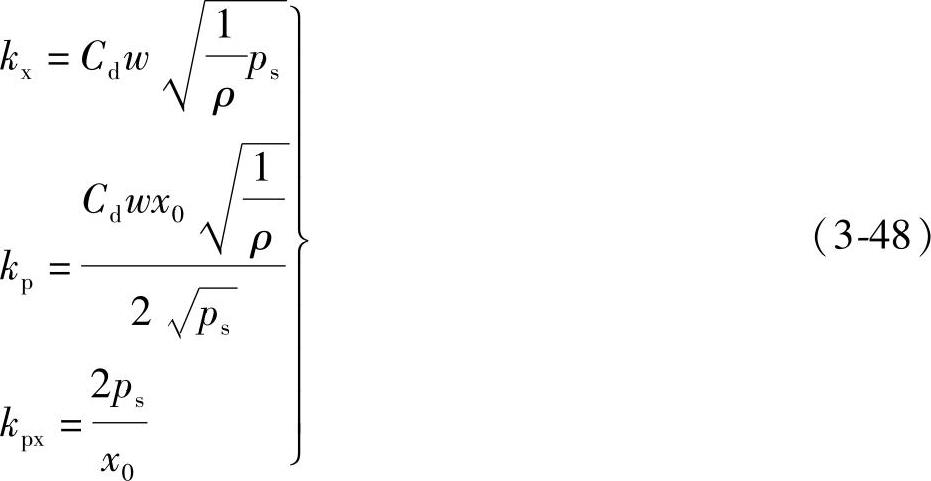
对比式(3-45)与式(3-48)发现,工作点压力选p10=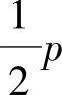 s时的三通阀流量增益与pL0=0时的零重叠四通阀的流量增益相等,而在同样条件下的三通阀流量-压力系数却是四通阀流量-压力系数的两倍,因此将使系统在常值负载力和摩擦负载力作用下的静差增加一倍。此外,由于压力灵敏度系数kpx较四通阀降低一半,因此三通阀的起动特性也较差。从动态分析,我们还可看到,由三通阀组成的动力机构的固有频率和相对阻尼系数也较四通阀为差。响应慢,动态误差比四通阀大一倍。由于三通阀的这些缺点抵消了其结构简单的优点,因此三通阀大部分使用在机液伺服系统中,因为机液系统的静态品质大都要求不高。
s时的三通阀流量增益与pL0=0时的零重叠四通阀的流量增益相等,而在同样条件下的三通阀流量-压力系数却是四通阀流量-压力系数的两倍,因此将使系统在常值负载力和摩擦负载力作用下的静差增加一倍。此外,由于压力灵敏度系数kpx较四通阀降低一半,因此三通阀的起动特性也较差。从动态分析,我们还可看到,由三通阀组成的动力机构的固有频率和相对阻尼系数也较四通阀为差。响应慢,动态误差比四通阀大一倍。由于三通阀的这些缺点抵消了其结构简单的优点,因此三通阀大部分使用在机液伺服系统中,因为机液系统的静态品质大都要求不高。
零重叠三通阀的零位系数的理论值可由式(3-45)和式(3-46)得出:kx=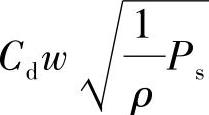 ;kp=0;kpx→∞。实际上正像零重叠四通阀一样,由于阀芯阀套之间存在着间隙,故零位泄漏仍然存在。仿照式(3-39)可得出
;kp=0;kpx→∞。实际上正像零重叠四通阀一样,由于阀芯阀套之间存在着间隙,故零位泄漏仍然存在。仿照式(3-39)可得出
 (https://www.xing528.com)
(https://www.xing528.com)
因为三通阀较四通阀窗口数目少一半。
压力灵敏度为

2.负重叠三通阀
由图3-10可以列出负重叠三通阀的综合特性方程(当xmax<Δ时)
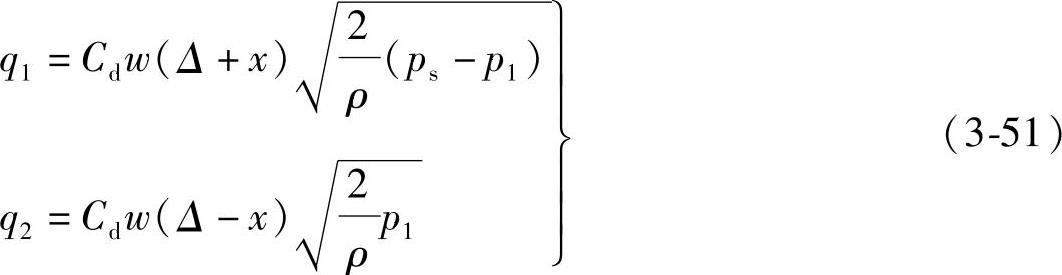
其负载流量方程为
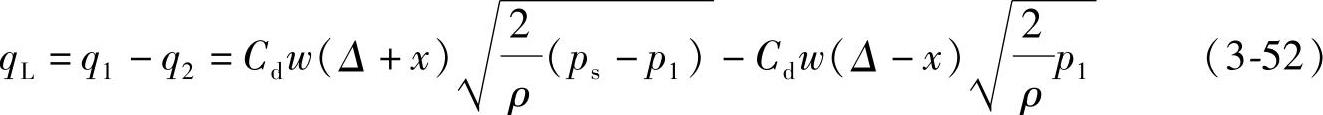
将式(3-52)化成无因次形式
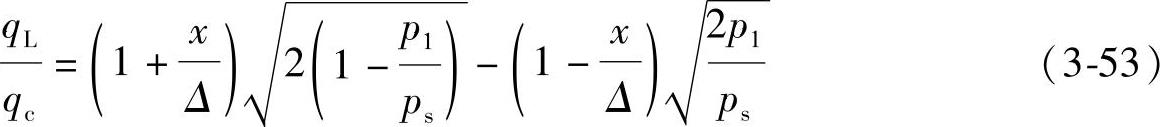
显然,按照式(3-53)即可画出负重叠三通阀的综合特性曲线。为了作图方便可将式(3-53)作如下变换,今设

将式(3-54)代入式(3-53)即可得到(3-24)式
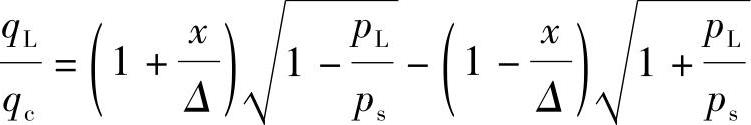
可见,负重叠三通阀的综合特性曲线的形状与负重叠四通阀综合特性曲线的形状完全相同。只是横坐标要相应地做如下变换:由式(3-54)可知,当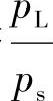 =+1时,
=+1时, =+1;当
=+1;当 =0时,
=0时,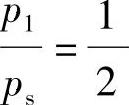 ;当
;当 =-1时,
=-1时, =0,……。因此,只要将图3-13的横坐标
=0,……。因此,只要将图3-13的横坐标 按式(3-54)变换成
按式(3-54)变换成 ,即构成负重叠三通阀的负载压力-流量曲线,如图3-21所示。
,即构成负重叠三通阀的负载压力-流量曲线,如图3-21所示。
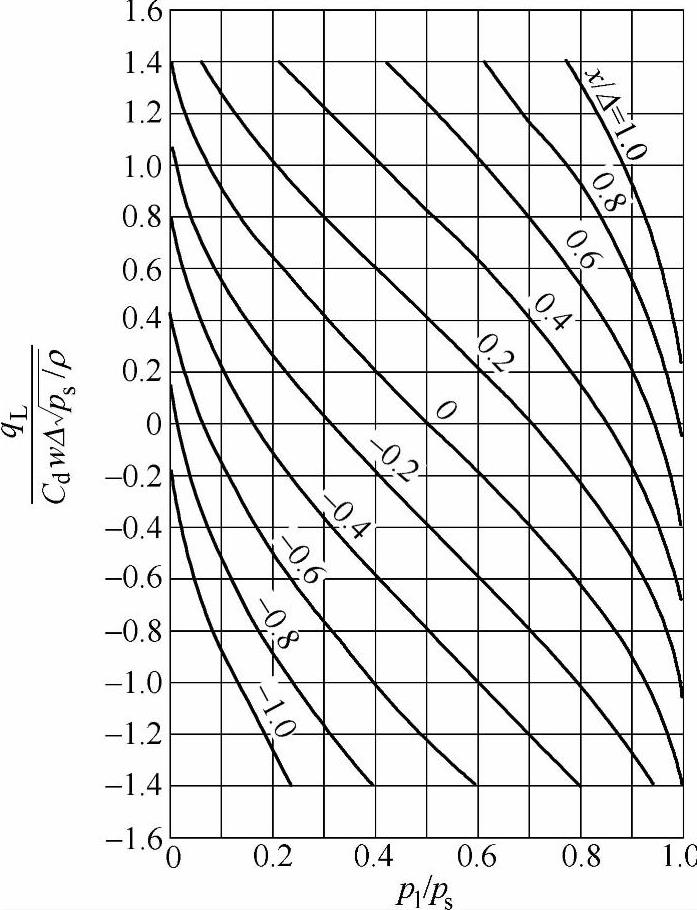
图3-21 负重叠三通阀的负载压力-流量曲线
负重叠三通阀的线性化增量方程可由式(3-52)得到
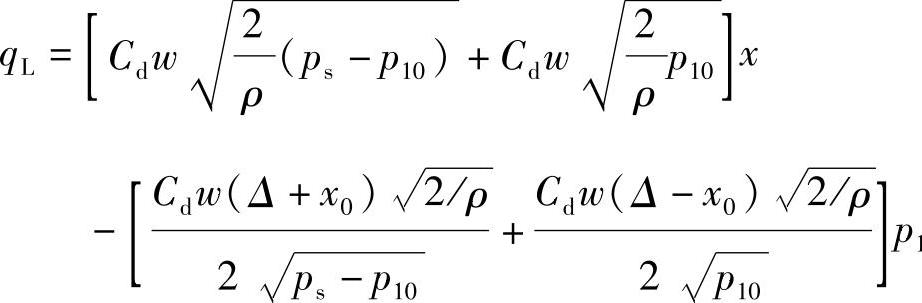
由此可得到
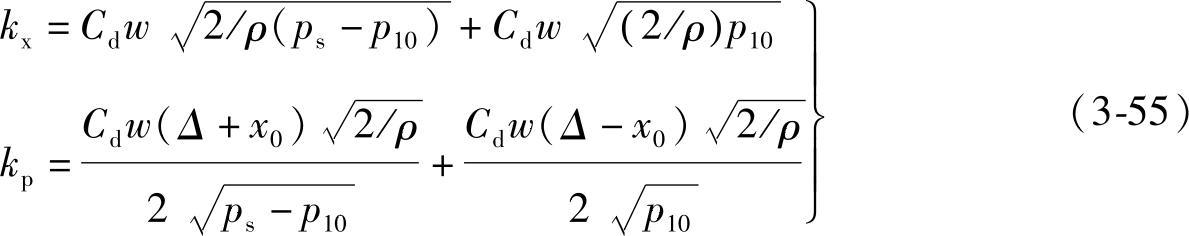
当选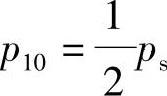 时,零位系数(qL0=x0=0)为
时,零位系数(qL0=x0=0)为
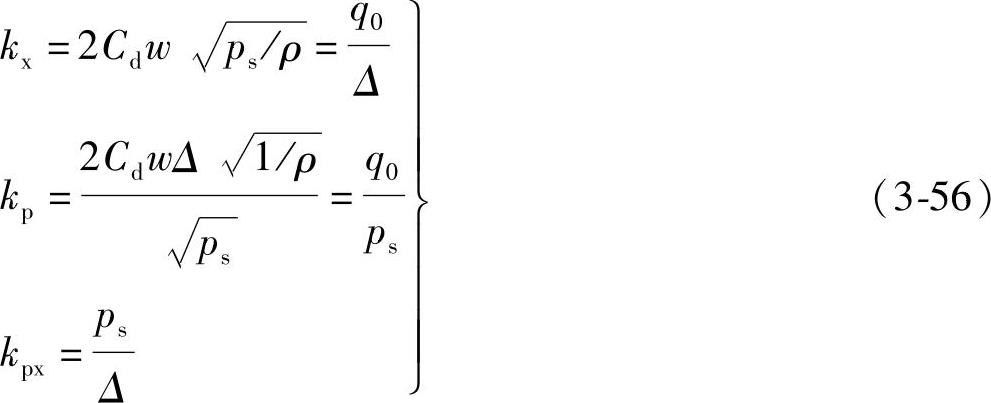
式中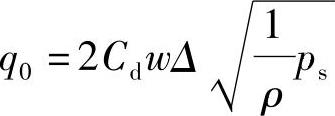
将式(3-56)和式(3-29)对比,所得出的结论与零重叠三通阀和零重叠四通阀对比所得到的结论完全一样。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




