负重叠四通阀的综合特性分析与优化

1.综合特性

图3-12为负重叠四通阀的原理图，其中图3-12a为结构图，图3-12b为液流通道可变液阻的等效液桥。当阀芯处在零位（x=0）时，进回油窗口都有一个宽度为Δ的正开口，通称预开口。此时四个节流窗口处的流量方程可根据伯努利方程得出（这里假设各窗口是配磨且对称的，而回油压力为零。在本章的全部讨论中都遵照这个假设条件）。

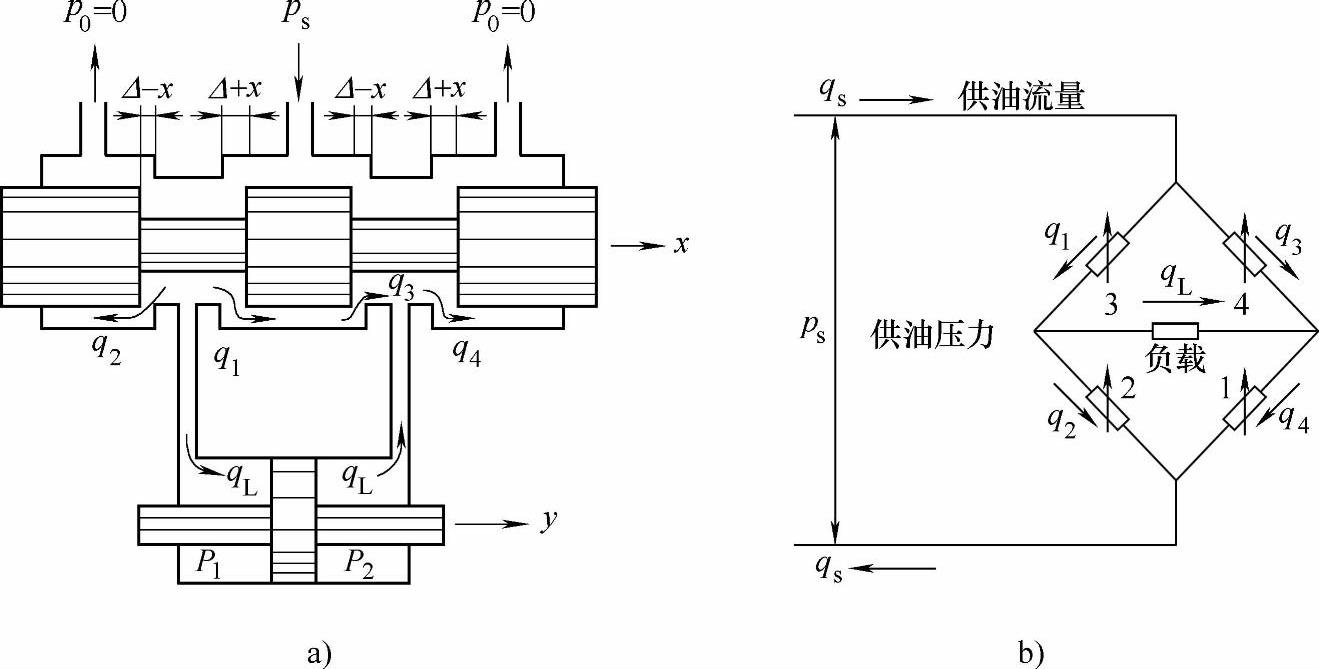
图3-12 负重叠四通滑阀原理图

a）工作原理图 b）可变液阻的等效液桥

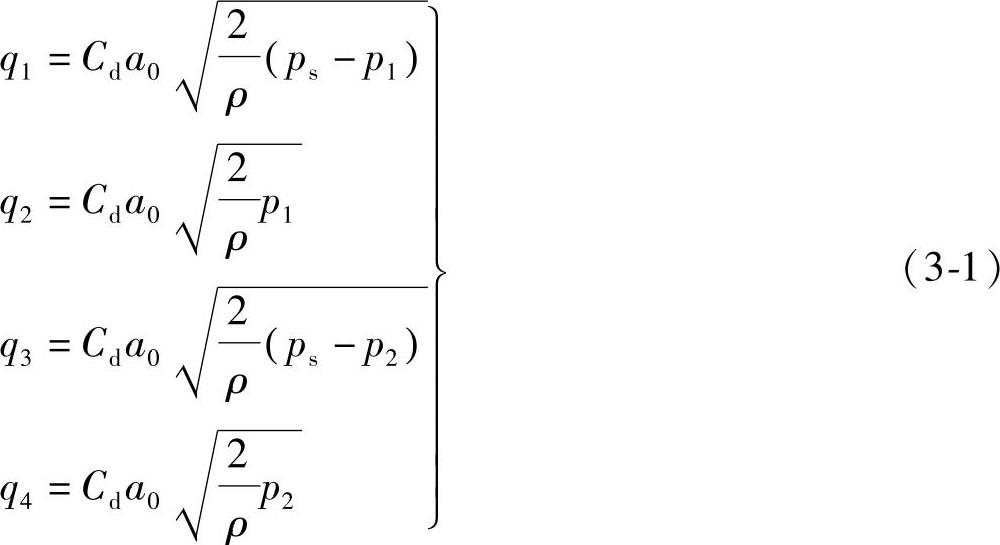
式中 a₀——窗口名义面积（m²），a₀=wΔ；

w——窗口面积梯度（m），对于圆周边开口的圆柱滑阀，w=πD，其中D为阀芯凸肩处直径（m）；

p₁——液压缸左腔液体的压力（Pa）；

p₂——液压缸右腔液体的压力（Pa）；

q₁——由油源流入液压缸左腔的流量（m³/s）；

q₂——由液压缸左腔流回油箱的流量（m³/s）；

q₃——由油源流入液压缸右腔的流量（m³/s）；

q₄——由液压缸右腔流回油箱的流量（m³/s）；

ρ——液体密度（kg/m³）；

C_d——流量系数。

若忽略液压缸及滑阀的各种泄漏及液体的可压缩性，可研究x=0时液压缸的运动状态。若设液压缸活塞在液压力作用下正以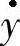的速度运动，则由此产生的流量为q_L，称之为负载流量。对于q_L，有

式中 A——液压缸活塞的有效面积（m²）。

将式（3-1）带入式（3-2）可得

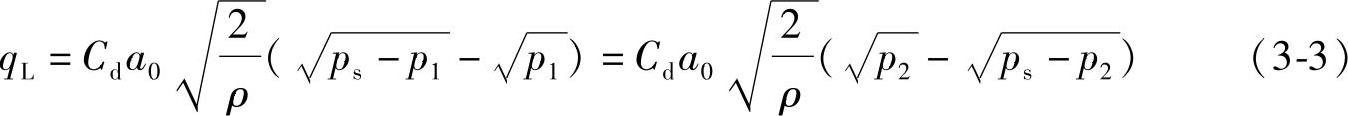
若设q_L>0，即活塞向右运动，则由式（3-3）左边得到不等式

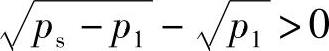
由此可得

p_s^-p1>p₁或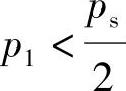（3-4）

同理，由式（3-3）右边也可得

p₂>p_s-p₂或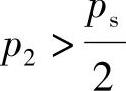（3-5）

由式（3-4）及式（3-5）可得p₂>p₁，这显然与假设的条件———活塞向右运动相矛盾，故此假设为伪。

若设q_L<0，即活塞向左运动，则由式（3-3）左边依同理可得p_s^-p1<p₁，或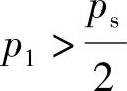（3-6）

由式（3-3）右边也可得

p₂<p_s-p₂，或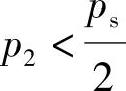（3-7）

由式（3-6）及式（3-7）可得p₂<p₁，这又与假设的条件———活塞向左运动相矛盾，故此假设也为伪。

若设q_L=0，即活塞停止运动，则由式（3-3）左边可得

由式（3-3）右边也可得

由式（3-8）及（3-9）两式可得，p₁=p₂，这与假设条件一致，故此假设为真。可见，当活塞运动速度y=0时，若作用在其上的载荷为零，则由四通阀与执行元件组成的动力机构无静差。以上的证明方法称之为归谬法。

当阀芯产生x位移时，（x≤Δ），每个窗口的开度由图3-12表示出来，此时流量方程分别为

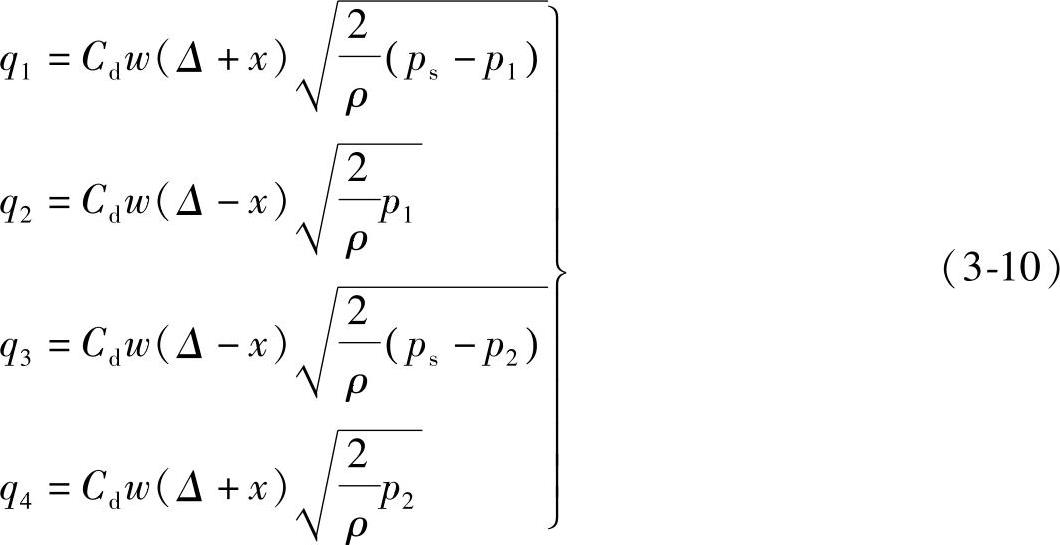
将式（3-10）代入式（3-2）得

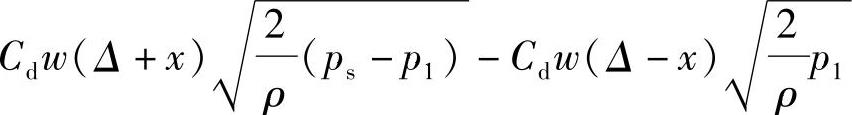
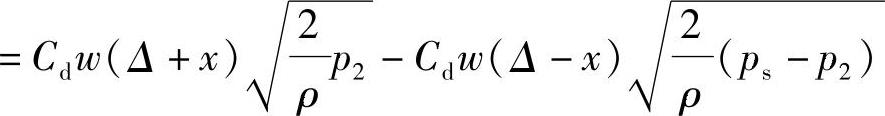
上式消去各项共有的C_d、w和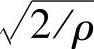，并移项可得到

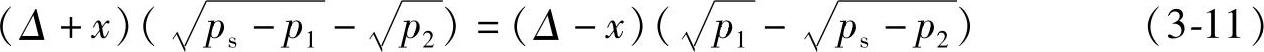
式（3-11）中p₁、p₂与p_s的关系也必须用归谬法加以判断。

若式（3-11）大于零，则由左边得到不等式

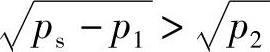
故 p_s-p₁>p₂或p₁+p₂<p_s（3-12）

由式（3-11）右边得到不等式

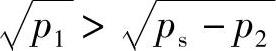
故 p₁>p_s-p₂或p₁+p₂>p_s（3-13）

由式（3-12）与式（3-13）得出矛盾结果，故假设为伪。(www.xing528.com)

若式（3-11）小于零，则依同理得出

左边：p_s-p₁<p₂或p₁+p₂>p_s（3-14）

右边：p₁<p_s-p₂或p₁+p₂<p_s（3-15）

显然，式（3-14）与式（3-15）也是矛盾的，因而此假设也为伪。

若式（3-11）等于零，则

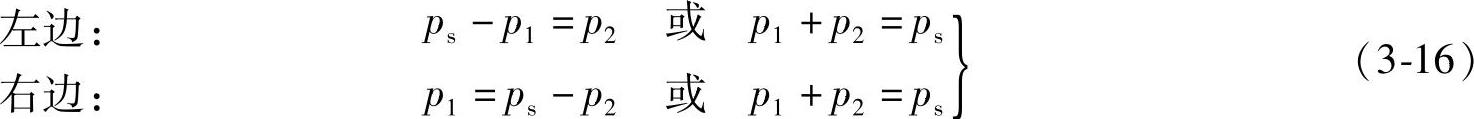
可见此假设为真。若设

p_L=p₁-p₂（3-17）

式中的p_L称为负载压力，由式（3-8）、式（3-9）和式（3-16）可看出负重叠四通滑阀在任何状态下p₁与p₂都满足下式

p₁+p₂=p_s（3-18）

将式（3-17）与式（3-18）联立得

将式（3-19）代入式（3-10）得到

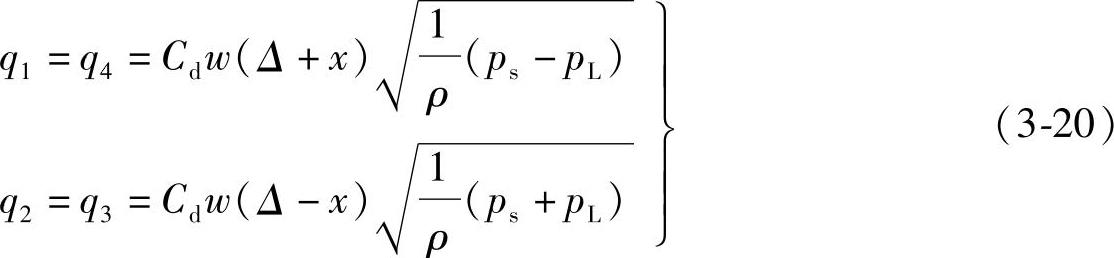
将式（3-20）代入式（3-2）得到负重叠四通滑阀的负载流量方程

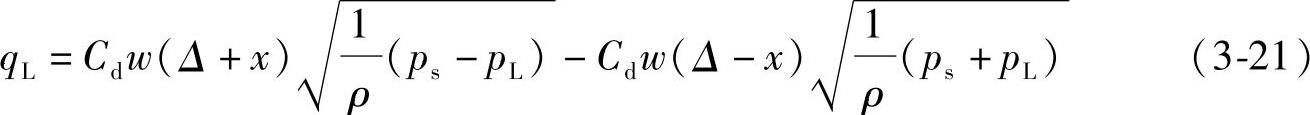
式（3-21）表示了q_L、p_L及x三个参数之间的函数关系，故也可称之为综合特性方程，或负载压力-流量方程。如果以负载流量为纵坐标，以负载压力为横坐标，以阀芯位移为参变量，便可画出综合特性曲线，通常称之为负载压力-流量曲线。为了作图的方便，一般将式（3-21）化成无因次形式，今将式（3-21）化成下列形式

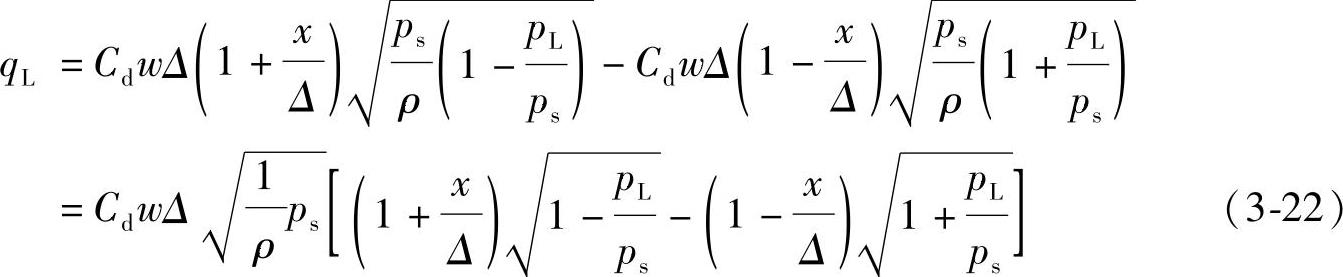
若令

则可将式（3-22）化成

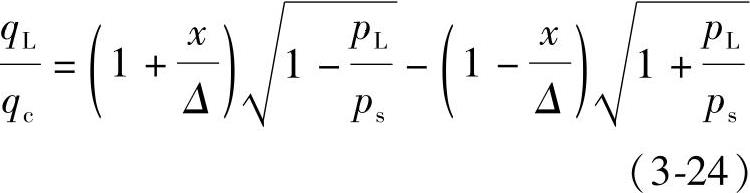
今以x/Δ为参变量，以q_L/q_c为纵坐标，以p_L/p_s为横坐标，便可画出负载压力^-流量曲线的无因次形式，如图3-13所示。

其具体做法是：任给一个x/Δ值，然后连续地改变比值p_L/p_s（一般p_L/p_s在-1～1之间取值），便得到一条无因次负载压力-流量曲线，若令x/Δ在-1～1之间依次取值，并重复上述步骤便可画出图3-13。

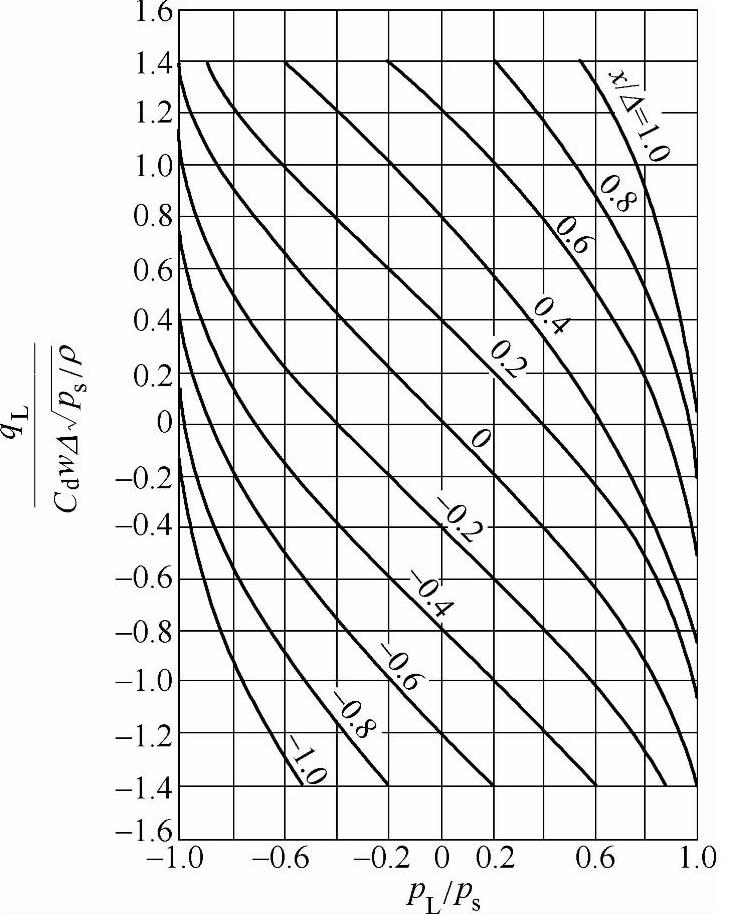
图3-13 负重叠四通滑阀的无因次负载压力-流量曲线

2.线性化方程

由式（3-21）看出，负载流量与负载压力之间是一种非线性关系，如果将其直接引入到液压控制系统中便会带来很多困难，因为线性控制理论此时已不适用，而非线性理论还没有统一的方法。因此，通常将这一类连续的非线性方程进行线性化处理，即将原方程在工作点处展成泰勒级数，并取其前两项，最后化成增量方程的形式。今将式（3-21）在工作点展成泰勒级数，并取其前两项，可得到下列增量方程

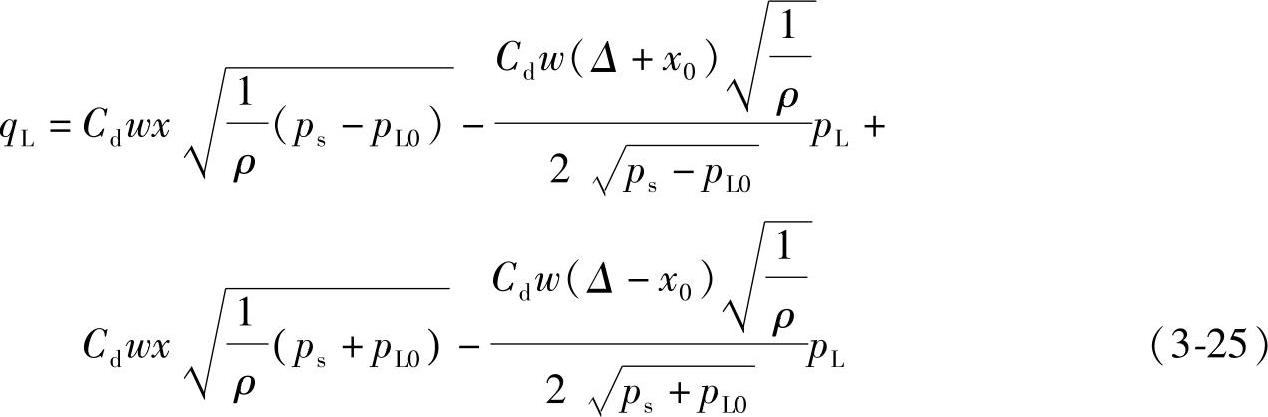
式中 x₀、p_L0———平衡工作点的稳态值。

若设k_x为阀口的流量增益，k_p为阀口的流量-压力系数，并有

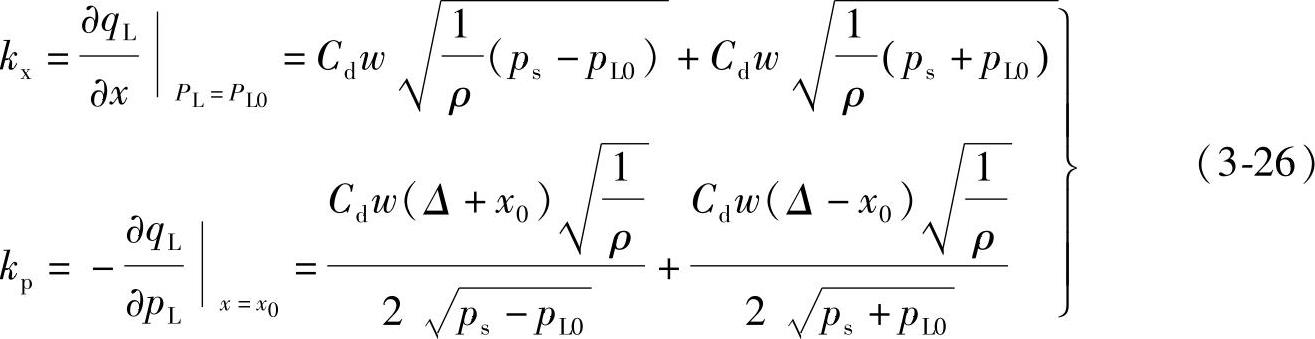
则式（3-25）可写成

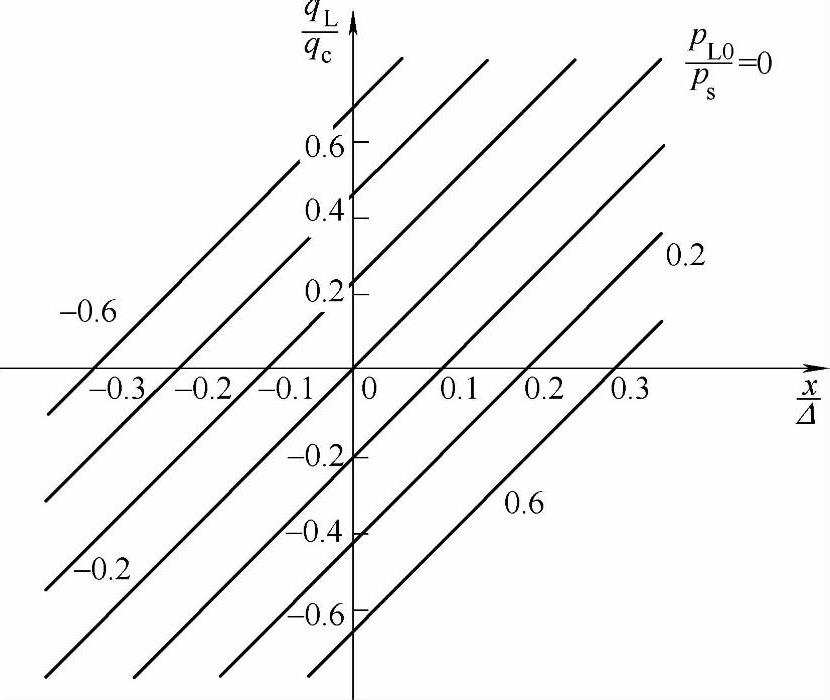
图3-14 以p_L为参变量的q_L-x流量曲线

q_L=k_xx-k_pp_L（3-27）式（3-27）便是负重叠四通阀的线性化增量方程式。参照式（3-26）及图3-13可以看出，k_x即是当负载压力p_L=p_L0时的q_L-x流量曲线的斜率，如图3-14所示。从图3-14可以看出，当以p_L为参变量时流量曲线为斜直线，而且斜率在一定范围内是相等的。由于流量增益k_x表示滑阀移动单位长度所引起的流量变化的大小（单位为m²/s），故它反应了滑阀对流量控制的灵敏程度；k_p称之为流量-压力系数，由图3-14看出，k_p即是当x=x₀时q_L-p_L曲线在p_L=p_L0点处的斜率，它表示在滑阀窗口开度一定的条件下，负载流量对负载压力变化的敏感程度[单位为（m⁵/s）·N]。在以后的讨论中可以看出，k_x与k_p对系统品质影响很大，前者影响到系统的开环增益大小，因而影响到系统的动态品质和静差；后者相当于一种阻尼，因此直接影响到系统的稳定性和动态品质。另外，k_p也相当于泄漏系数，故对系统的刚度影响较大。

滑阀除了上述两个重要系数外，还有一个所谓压力灵敏度系数k_px（也称为压力增益）。对于k_px，有

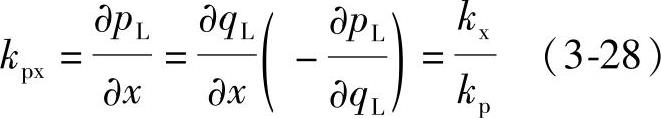
k_px乃是当负载流量q_L=q_L0时p_L-x曲线的斜率。由图3-15看出对于负重叠四通阀来说，k_px是压力特性曲线的切线斜率，通常压力增益（压力灵敏度）指q_L=0时阀单位输入位移所引起的负载压力变化大小。此值大，阀对负载压力控制灵敏度高。k_px在一定范围内基本上是个常数。k_px代表了动力机构的起动特性，k_px越大动力机构的起动特性越好。

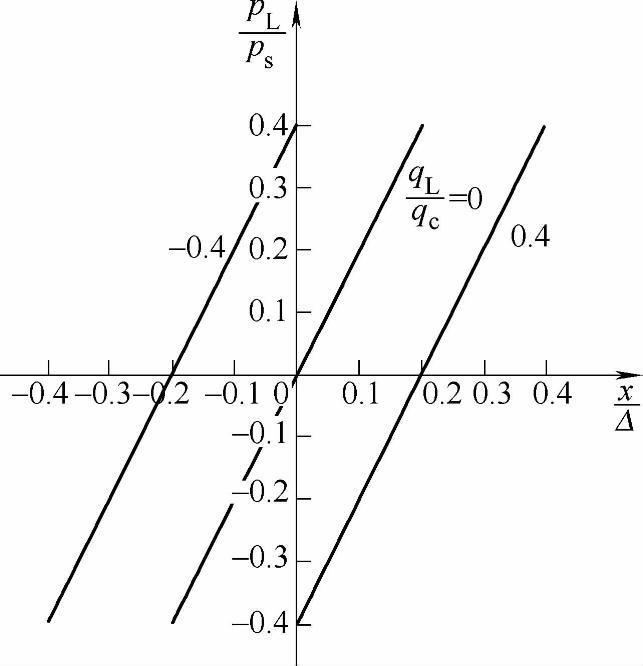
图3-15 以q_L为参变量的p_L-x曲线

3.阀系数的确定

由式（3-26）及式（3-28）看出，滑阀的系数与工作点的选择有关，若取p_L0=x₀=0为工作点，则由式（3-26）及式（3-28）两式可得出

式（3-29）称之为负重叠四通滑阀的零位系数。其定义为：流量增益k_x表示负载压降一定时，阀输入单位位移所产生的负载流量。k_x越大，阀对负载流量的控制越灵敏。压力增益k_px表示负载流量一定时，阀输入单位位移所引起的负载压降的变化量，k_px越大，表示起动负载的能力越强。流量-压力系数k_p表示阀的开口一定时，负载单位压降的变化引起负载流量变化的大小。k_p越大，说明负载很小的变化就会引起负载流量很大的变化，即阀的刚性差，所以k_p又叫阀刚度。

以上我们用归谬法证明了负载流量方程以及三个阀系数，研究了q、p及x三个参数之间的函数关系，可以看出这种方法简洁明了，逻辑严谨，非常直观。我们也可以利用液桥关系方程来证明，得到完全相同的方程和关系式，但由于各桥臂的流量方程是非线性的，因此这些方程联解起来很麻烦，而且使一般公式无法简化，难以应用于实际。所以，在后面的讨论和证明中，除特别说明外，我们仍用归谬法来解决。

4.特性分析

1）阀的三个系数是表征阀静态特性的三个性能参数，它们在确定系统的稳定性、响应特性时是非常重要的。流量增益直接影响系统的开环放大系数，因而对系统的稳定性、响应特性和稳态误差有直接的影响。流量-压力系数直接影响阀-液压马达组合的阻尼系数和速度刚性。压力增益标志着阀-液压马达组合起动大惯量或大摩擦负载的能力，阀的这个参数可以达到很高的数值，这正是伺服系统所希望的特性。这些结论在以后的讨论中还会逐步地明确起来。

2）阀的系数的数值随工作点的变化而变化。最重要的工作点是压力-流量曲线的原点（即在q_L=q_L0=x₀=0处），因为系统（位置控制系统）经常在原点附近工作，此处阀（矩形窗口）的流量增益最大，因而系统的增益最高；但流量-压力系数最小，所以阻尼最低。因此，从稳定性的观点来看，这一点是最关键的。如果系统在这一点是稳定的，则在其他各工作点也是稳定的。在原点附近的阀系数称为零位阀系数，分别以k_x、k_p、k_px表示。若工作点在原点，则增量和变量相等，压力^-流量特性的线性化表达式如式（3-27）所示。

3）线性化方程式（3-27）的精确度和适用范围与变量的变化和阀特性的线性度有关。变量的变化范围小，线性化的精确度就高；阀特性的线性度高，所允许的变量变化范围就大。

以上有关四通阀的讨论具有普遍的意义，所用的分析方法和基本概念对所有节流原理工作的阀都适用，无论是滑阀、挡板阀还是其他类型的阀。