【摘要】：+an=0则系统稳定的条件是：1）诸系数ai>0（i=0，1，2，…图2-16 稳定系统与不稳定系统的被调量曲线即以上判别条件称之为古尔维茨判据，按照此判据可以方便地得出4阶以下系统的稳定性判别式，见表2-2。表2-24 阶以下系统的稳定条件2.频率辨别法如果系统开环对数幅频特性在大于零的区间内对应的相频特性曲线穿越了-π的横线，闭环系统即是不稳定的，否则就是稳定的，这种判别条件称为对数频率判据。
系统稳定的充要条件是系统传递函数分母（通称为闭环特征方程）的根的实部都为负数。但解高次代数方程是困难的，因此希望利用间接的方法来判别系统的稳定性。一般常用的有代数判别法和频率判别法，下面分别加以介绍。
1.代数判别法
若系统闭环特征方程式为
a0sn+a1 sn-1+…+an=0（2-37）
则系统稳定的条件是：
1）诸系数ai>0（i=0，1，2，…，n）。
2）诸行列式Hi>0（i=2，3，4，…，n）。
图2-16 稳定系统与不稳定系统的被调量曲线
即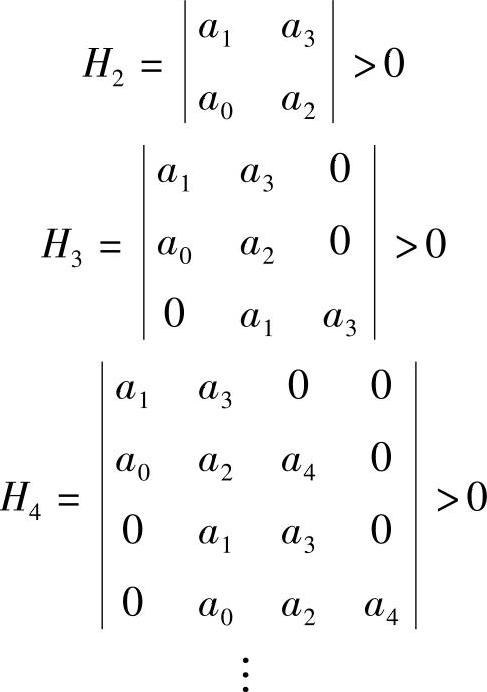
(www.xing528.com)
以上判别条件称之为古尔维茨判据，按照此判据可以方便地得出4阶以下系统的稳定性判别式，见表2-2。
表2-24 阶以下系统的稳定条件
2.频率辨别法
如果系统开环对数幅频特性在大于零的区间内对应的相频特性曲线穿越了-π（-180°）的横线，闭环系统即是不稳定的，否则就是稳定的，这种判别条件称为对数频率判据。所谓开环频率特性是指系统从输入到反馈之间的频率特性，例如图2-11a所示的开环频率特性即是W1（jω）·W2（jω）。图2-17a所代表的系统是稳定的，而图2-17b所代表的系统便是不稳定的。
图2-17 稳定系统与不稳定系统的开环对数频率特性曲线
a）稳定系统 b）不稳定系统
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
