几种典型环节的传递函数的介绍

1.比例环节

所谓比例环节即指其输入、输出量之间呈比例关系的环节。在液压控制系统中常见的比例环节有下列三种：

（1）运算放大器 运算放大器是电液控制系统中必须用到的一种电子放大器。图2-1为运算放大器原理图，其输入端的电流方程为

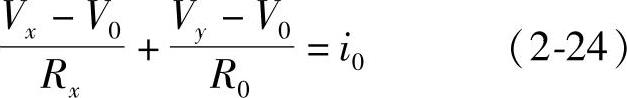
式中 V_x——输入电压；

V_y——输出电压；

V₀——输入端对地电压；

R₀——反馈电阻；

i₀——输入端的电流。

因为 V_y=-μV₀

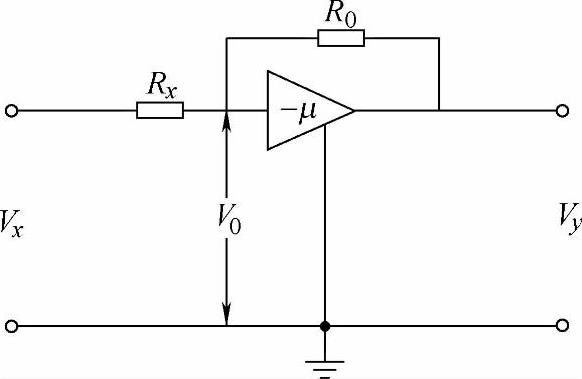
图2-1 运算放大器原理图

式中 μ——开环增益。

故

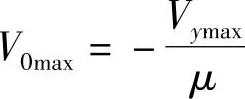
由于V_ymax一般为100V，或者10V，而μ=10⁸～10¹¹，故V_0max=10^-6～10^-10V，因而V₀可以忽略；另外，输入端的电流通常为微安级，故也可以略去。因此式（2-24）可近似写成

V_x/R_x=V_y/R₀

或

V_y=-KV_x（2-25）

式中的K=R₀/R_x称为比例常数或放大系数。

（2）位移放大器 图2-2为液压位移放大器，若忽略液体泄漏及可压缩性，可列出下列方程

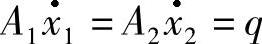
两边积分得

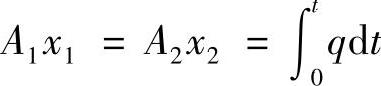
故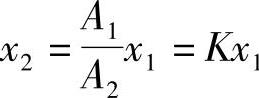（2-26）

式中 K=A₁/A₂。

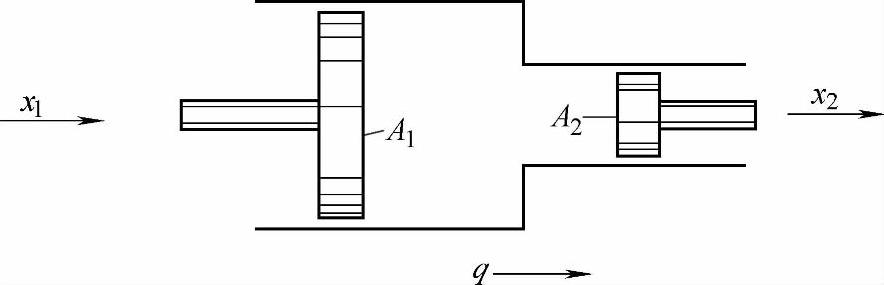
图2-2 液压位移放大器

（3）压力放大器 图2-3为增压器——压力放大器，若忽略各种阻尼力，则

A_1p1=A₂p₂

故 p₂=Kp₁（2-27）

式中 K=A₁/A₂。

比例环节的特点是输出与输入之间无时间滞后与波形失真。

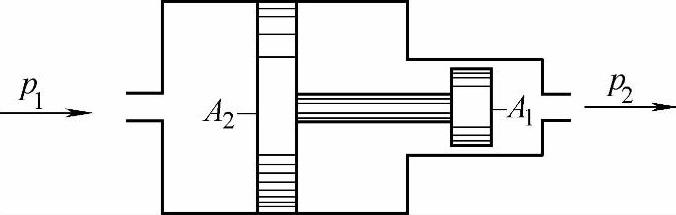
图2-3 增压器原理图

2.惯性环节

（1）电网络 图2-4为利用运算放大器组成的惯性环节，按照前面介绍的计算公式可得到（仍设V₀=i₀=0）

则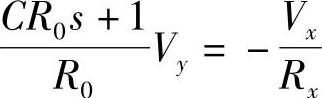

故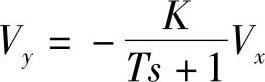（2-29）

式中 C——反馈电容。

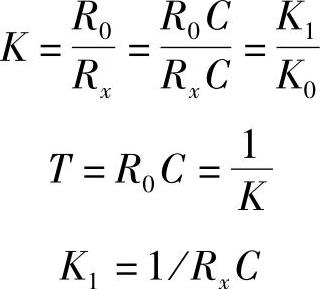
式中 K₁——输入端的增益。

K₀=1/R₀C

式中 K₀——反馈端的增益。

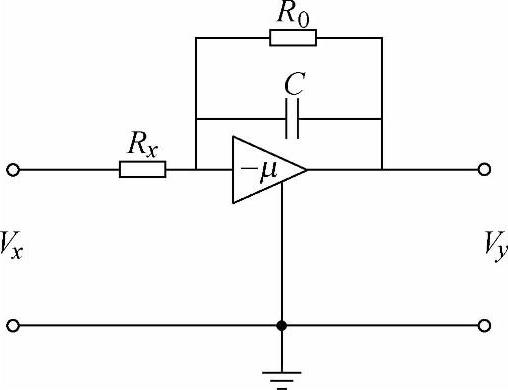
图2-4 由电网络组成的惯性环节

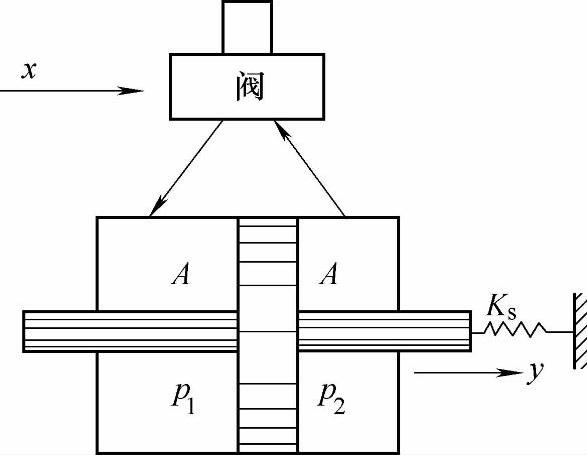
图2-5 带有弹性负载的阀控液压缸动力机构

（2）带有弹簧负载的阀控液压缸式动力机构 图2-5是带有弹簧负载的阀控液压缸式动力机构。若忽略液容效应及泄漏，并且只考虑弹性负载，则其流量方程为

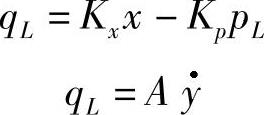(www.xing528.com)

力方程为 Ap_L=K_ay

以上三式联立，消去q_L及p_L，可得到

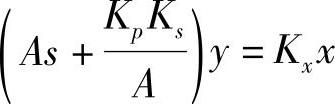
则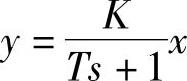（2-30）

式中 x——伺服阀阀芯位移（m）；

K=K_xA/K_pK_s；

T=A²/K_pK_a；

A——活塞有效面积（m²）。

惯性环节的传递函数为W（s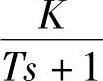）=，一般由一个储能元件和一个耗能元件组成，其输出与输入之间存在着时间上的滞后，T称之为时间常数，K为增益。

3.积分环节

（1）电网络——积分放大器 图2-6为积分放大器，其电流方程可由式（2_-28）得到（令R₀→∞）

C_sV_y=-V_x/R_x

故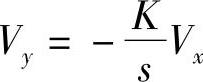（2-31）

式中 K=1/CR_x。

（2）无负载的阀控液压缸 图2-7为无负载的阀控液压缸，若忽略液容效应和泄漏，可列出其流量方程

q_L=A_sy=K_xx-K_pp_L=K_xx（因无负载，p_L=0）

故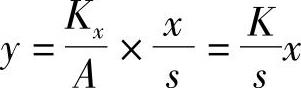（2-32）

式中 K=K_x/A。

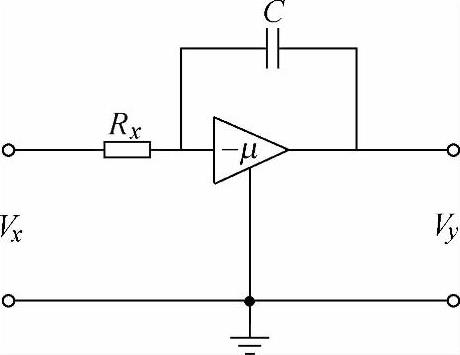
图2-6 积分放大器原理图

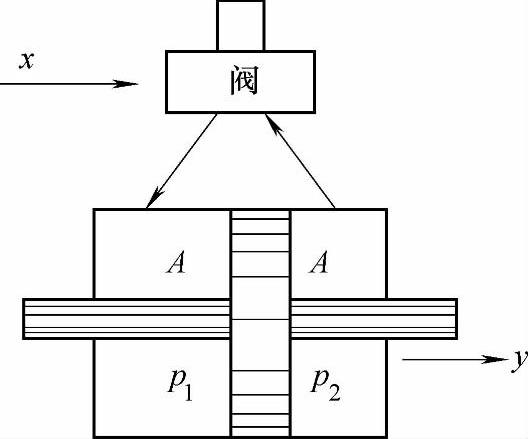
图2-7 无负载的阀控液压缸示意图

积分环节的传递函数为W（s）=K/s，其输出函数等于输入函数的积分，即输出量为输入量对时间的累积，输出幅值呈线性增长。因此，在系统中凡有储存或累积特点的元件，都有积分环节的特性。

4.微分环节

若环节的输出量与输入量的导数成正比，则称为微分环节，可由下面数学表达式描述

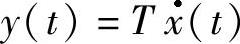
经拉氏变换后，得

Y（s）=TsX（s）

传递函数为

式中 T——时间常数。

微分环节在实际工程中很难构建，只能近似实现。也就是说，只有当惯性作用较弱，而微分作用很强时，才可以近似看作一个微分环节。

5.振荡环节

凡振荡环节都能用二阶微分方程来描述，其数学表达式为

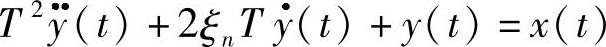
经拉氏变换后，得

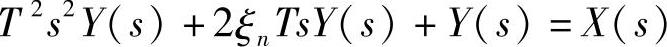
传递函数为

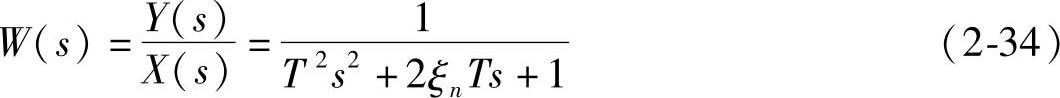
令ω_n=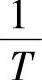，代入（2-34）化简后得

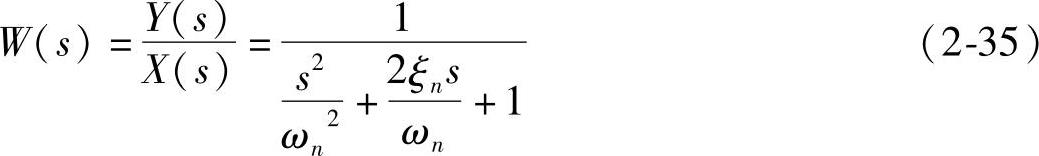
式中 ω_n——无阻尼固有频率；

ξ_n——阻尼比。

二阶振荡环节一般含有两个储能元件和一个耗能元件，由于两个储能元件之间有能量交换，就可能使系统的输出发生振荡。在实际工程中，液压系统的振荡网络是很多的，如阀控液压缸和阀控液压马达动力机构等，往往会形成振荡环节。

6.滞后环节

凡是输出信号对于输入信号的响应，滞后一段时间τ的环节，称为滞后环节。例如，如果忽略液容效应、管壁变形及液体中的气体，则液体在管道中由一端传到另一端时，相位滞后了ωτ，但波形并没有变化，因此可以将管子看成一个环节——滞后环节。其动态方程式的拉氏变换形式为

Y（s）=e-τsX（s）

故其传递函数为

W（s）=e-τs（2-36）

滞后环节在系统中是有害的，它影响系统的稳定性，因此对液压控制系统而言，应尽量减小管路的长度。