传递函数的定义及应用

如果一个系统或元件的输出量与输入量的初始条件都为零，则它们的拉氏变换之比称为传递函数。设系统的输入量为x（t），输出量为y（t），则它的传递函数W（s）是输出量的拉氏变换Y（s）与输入量的拉氏变换X（s）之比

则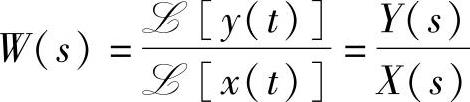（2-20）

传递函数的求取方法，对于一般的环节或简单的系统则可以由它们的微分方程进行拉氏变换求得。对于复杂的环节和系统，则可先求出环节或部件的传递函数，绘制系统的功能图，然后利用功能图的有关运算规则来计算总的传递函数。

对于线性定常系统的线性常微分方程一般可表达为

当初始条件为零时，对微分方程两边进行拉氏变换后得(www.xing528.com)

则系统的传递函数

由式（2-23）可见，只要将系统运动方程中的微分算子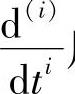用相应的s（i）来代替，便可得到系统传递函数的表达式，其中i=1，2，3，…，n为微分方程的阶次。所以，传递函数的形式完全取决于运动方程的形式。也就是说，f（t）与F（s）之间有一一对应的关系，我们不研究f（t）的特性，而只研究F（s）的特性。

传递函数表示了从输入到输出之间在复域中信息的传递关系，表达了系统本身的固有特性，与输入量和初始条件等外部因素无关，只有系统的输出响应Y（s）才与输入量X（s）和初始条件等有关。传递函数仅仅描述系统的动态特性而不涉及系统的物理模型，对于机械的、电气的、液压的等不同的物理模型可以具有相同的传递函数。