【摘要】：在运用拉氏变换求解微分方程的时候，借助一些定理可以简化运算，现介绍如下。即则3.微分定理如果函数f及其各阶导数的起始条件都为零，而且在t>0时是可微的，则上式表明通过拉氏变换可以将微分运算变成乘积运算。
在运用拉氏变换求解微分方程的时候，借助一些定理可以简化运算，现介绍如下。
1.叠加定理
两个函数之和的拉氏变换等于两个函数拉氏变换之和。
若f（t）=f1（t）±f2（t）
则
或写成F（s）=F1（s）±F2（s）（2-12）
2.比例定理
如果原函数放大k倍，k为一常数而不是t的函数时，那么象函数也放大k倍。
即
则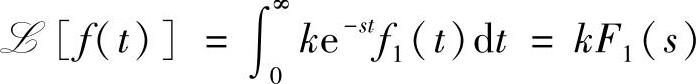
（2-13）
3.微分定理
如果函数f（t）及其各阶导数的起始条件都为零，而且在t>0时是可微的，则
上式表明通过拉氏变换可以将微分运算变成乘积运算。例如，下列微分方程的拉氏变换可以运算如下(www.xing528.com)
设
则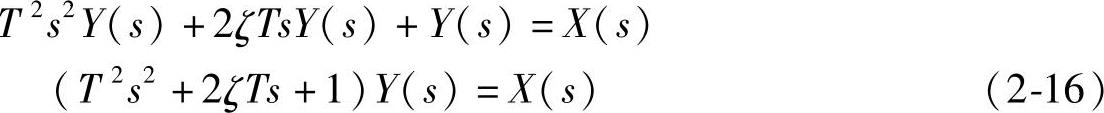
4.位移定理
若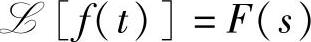
，则对任一常数a，f（t）与e-at相乘后的拉氏变换为
由式（2-17）看出，对于e-atf（t）一类的函数，它的象函数只需把s用s+a代替即可。
5.初值定理
若函数f（t）的象函数为F（s），如果时间函数的极限存在，则初值定理可表示为
式（2-18）表明，原函数f（t）在t=0时的数值，可以通过将象函数乘以s以后，再求s→∞的极限值来获得。因此，利用初值定理可以从象函数直接找出原函数在t=0时的数值。
6.终值定理
如果函数f（t）的拉氏变换为F（s），则终值定理可表示为
式（2-19）表明f（t）的终值等于其拉氏变换的初值。这一定理对于求取液压控制系统的静差很有用。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
