拉氏变换的基本概念的介绍

为了研究自动控制系统，经常需求解描述系统的线性微分方程式。按照一般方法求解，比较麻烦，特别是求解高阶微分方程时就更加困难。采用拉普拉斯变换（简称拉氏变换）方法可使方程的求解简化。

拉氏变换实际上是一种函数变换，例如，用对数的方法就可把乘除法的运算变成加减法的运算，把乘方、开方的运算变成乘除法的运算，如

x=ab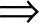lgx=lga+lgb

x=aⁿb^m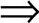lgx=nlga+mlgb

变换后的函数lgx、lga和lgb等是有明确意义的，它是10的幂数，因为数的乘除相当于原函数化为对数后的幂数加减，这样就大大简化了运算。而且这里求取函数的变换和反变换可利用对数表来查找，给运算带来了许多方便。

拉氏变换方法与此相类似，它是将时间域的原函数f（t）变换成复变量s域的象函数F（s），将时间域的微分方程变换成复数域的代数方程，然后通过代数运算，求出变量为s的代数方程解，再通过反变换得到变量为t的原函数的解。

数学上将时间函数f（t）的拉氏变换定义为下述积分

拉氏变换中的自变量s是一个复数，通常称为拉氏变换算子，s=σ+jω。(www.xing528.com)

实质上，拉普拉斯变换可以理解为连续时间函数与给定函数e^-st乘积的积分运算，也就是对已知时间函数f（t），可以构造一个积分函数F（s），f（t）称为原函数，F（s）称为象函数，原函数与象函数之间有一一对应的关系。例如f（t）=e^-at，则象函数

经过拉氏变换后，可以把一些较复杂的函数化为简单函数。

从数学上分析，并不是任何一个函数都可以利用拉氏变换的，它必须满足一定的条件，即：

1）当t＜0时，f（t）=0。

2）在任一有限区间上，f（t）分段连续、且有有限个间断点。

在工程技术上，如研究自动控制系统时，许多以时间t作为自变量的函数往往在t<0时是无意义的或根本不需要考虑的，也就是可把t<0时各时间函数均设为零。另外，自动控制系统中时间函数f（t）的不连续点一般是有限的，所以拉氏变换的积分是存在的，可以满足上述两个条件，故可应用拉氏变换法对其微分方程求解。