推算坐标方位角的方法

测量工作中并不直接测定每条直线的坐标方位角，而是通过一已知直线的坐标方位角，根据该直线与某一直线所夹的水平角，推算某一直线的坐标方位角。如图5.7所示。折线1—2—3—4—5 所夹的水平角β1、β2、β3，称为转折角，在推算时，β角有左角和右角之分，左角（右角）是指该角位于推算前进方向左侧（右侧）的水平夹角。

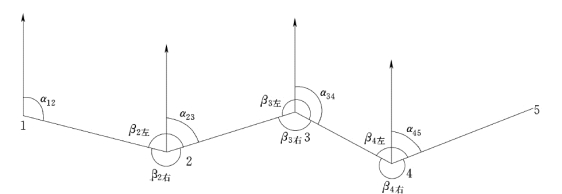
图5.7　方位角推算

1.相邻两条边坐标方位角的推算

设α12为已知方位角，各转折角为左角。

同理有：

由此可以得出按左角推算相邻边坐标方位角的计算公式为：

根据左、右角间的关系：将β左＝360°-β右代入式（5.14），则有：

综合式（5.14）和式（5.15）可得出相邻两条边坐标方位角的计算公式为：

2.任意边坐标方位角的推算(www.xing528.com)

将式（5.10）、式（5.11）、式（5.12）、式（5.13）左、右两边依次相加到所求的边，可得：

式（5.17）即为坐标方位角推算公式的表达式。

不难看出，式（5.16）是式（5.17）的特殊情况。

使用公式计算时，需要注意以下问题：

（1）式（5.17）中β前“±”的取法：当β为左角时取“＋”，当β为右角时取“-”。

（2）实际计算时，可根据坐标方位角的范围在0°～360°这一特征，n×180°前的“±”可以任意取“＋”或“-”，随之坐标方位角可能出现大于360°或负值的两种情况，此时，可以通过±n×360°，使坐标方位角取值在0°～360°范围内。

（3）式（5.17）中，β角是从起始边（已知方向）所在终点的转折角开始连续计算到终边（所求方向）始点的转折角。

（4）若n 为偶数，在计算中可以不考虑±n×180°；若n 为奇数，计算中可以只考虑±1×180°，而使计算工作简化。

例5.3 图5.7中，已知α12＝100°，β2左＝110°，β3左＝240°，β4左＝100°，求α45。

根据式（5.17）可得：

化为0°～360°之内的角值为α45＝1110°-6×180°＝30°

或

可见，不管式（5.17）中±n×180°取“＋”还是取“-”计算结果完全相同。