换面法是保持原先几何元素不动的情况下,通过改变投影面的位置,使新的投影面与几何元素处于有利于解题位置。新投影面的选择应符合以下两个条件:(1)新投影面必须处于有利于解题。(2)新投影面必须垂直于原来投影体系中那个保留的投影面,组成一个新的两面投影体系。熟练掌握变换投影面的基本规律,掌握变换投影面法中解决的六个基本问题。通过投影变换,可以求解直线、平面图形的实长和实形;解决一些角度、距离的度量问题。换面时,要注意每次只能变换一个投影面;对于多次换面时,要注意对不同的投影面(如V面或H面)交替进行换面。换面法的关键是选择新的投影面使其处于有利于解题的位置,新投影面与保留投影面必须垂直。
【问题十八】 怎样利用换面法求直线实长与夹角?
1-26 用换面法求图1-26(a)线段CD的实长及对V面的倾角。
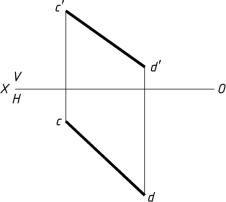
图1-26(a)
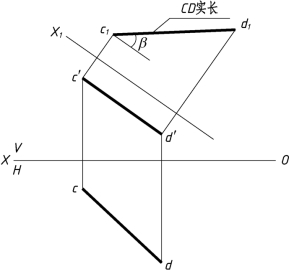
图1-26(b)
【解题分析】
要求一般位置直线的实长及对投影面的夹角需将直线通过一次换面变为投影面的平行线,如果是β角,则要保留V面,换掉H面。
【作图步骤】
(1)作新投影轴X1∥c′d′。
(2)按照点的变换规律,求出c1,d1。
(3)连接c1d1,则c1d1等于CD实长;c1d1与新投影轴X1的夹角就是CD直线与V面的夹角β角。
答案如图1-26(b)所示。
【问题十九】 怎样利用换面法求平面实形?
1-27 用换面法求四边形ABCD的实形。
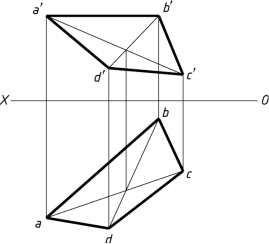
图1-27(a)
【解题分析】
将一般位置平面变换成投影面的平行面,需要进行两次变换。先将投影面的倾斜面变换成投影面的垂直面,再将其变换成投影面的平行面,即可求出平面的实形。
【作图步骤】
(1)AB为平面ABCD上的一条水平直线,作新投影轴X1⊥ab。
(2)按照点的变换规律,求出ABCD的垂直面a′1b′1c′1d′1。
(3)再作新投影轴X2∥a′1b′1c′1d′1。
(4)按照点的变换规律,求出a2、b2、c2、d2各点并连接之,即为所求。
答案如图1-27(b)所示。
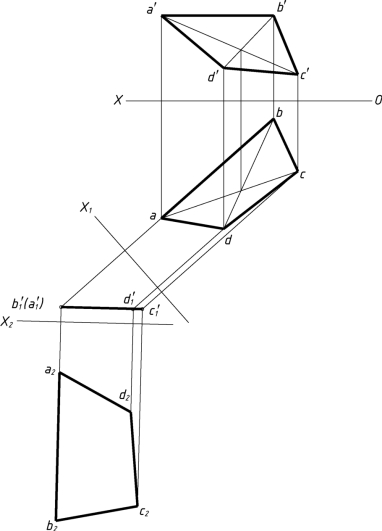
图1-27(b)
1-28 已知线段AB的实长,用换面法求其水平投影,本题有几个解答?请画出来。
【解题分析】
将一般位置直线变换成要投影面的平行线,需一次换面。此题有两种解法。
【作图步骤】
(1)作新投影轴X1∥a′b′,求出a1。
(2)以a1为圆心,以AB实长为半径交投影线得b1。
(3)按照点的变换规律,求出b,即为所求。
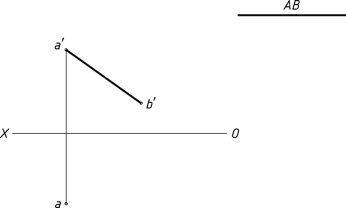
图1-28(a)
答案如图1-28(b)所示。
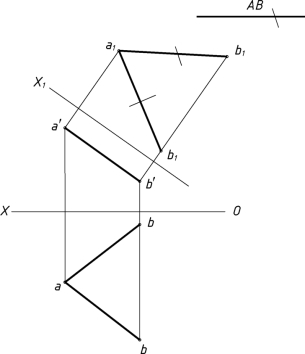
图1-28(b)
【问题二十】 怎样利用换面法求空间两直线的距离?
1-29 用换面法求平行两直线AB和CD之间的距离。
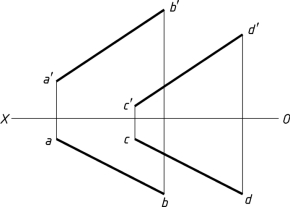
图1-29(a)
【解题分析】
当两平行线处于投影面垂直线位置时,可反映两平行线之间的距离实长,通过换面把AB和CD换成投影面垂直线,即可求解。
【作图步骤】
(1)确定X1轴,作新投影轴X1∥ab,把AB、CD换成投影面平行线,得到a′1b′1和c′1d′1。
(2)确定X2轴,作新投影轴X2⊥ab;把AB、CD换成投影面垂直线,得到a2b2和c2d2。
(3)连接点a2(b2)和点c2(d2)即为距离实长。
(4)求b′1e′1,b′e′∥O2X2轴。
(5)求be,最后求出b′e′。
答案如图1-29(b)所示。(https://www.xing528.com)
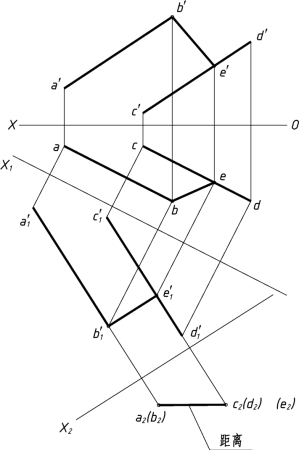
图1-29(b)
1-30 已知直线AB∥CD,且相距为L,用换面法求c′d′。本题有几种解法?请画出来。
【解题分析】
必须把AB、CD两平行线都变换成投影面垂直线,再根据两平行线之间的距离实长,求出积聚性的投影(此为解题关键)。根据投影变换规律,最后求出H面和V面的投影,即可求解。
【作图步骤】
(1)确定X1轴,作新投影轴X1∥ab,把AB换成投影面平行线,得到a′1b′1。
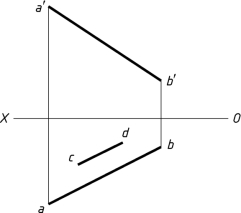
图1-30(a)
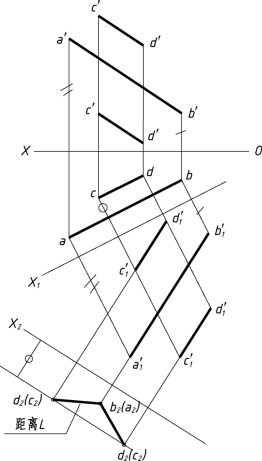
图1-30(b)
(2)确定X2轴,作新投影轴X2⊥a′1b′1;把AB变换成投影面垂直线,得b2(a2)。
(3)以b2(a2)为圆心,距离L为半径画圆。
(4)作一平行于X2轴的直线,它们间的距离等于cd与X1轴间距离。交圆得b2(c2),有两种解法。
(5)最后求c′d′。
故此题有两种解法。
答案如图1-30(b)所示。
1-31 用换面法补全以AB为底边的等腰三角形ABC的水平投影。
【解题分析】
等腰三角形的高线具有垂直并等分底边的几何性质。根据直角投影定理,当相交两直线互相垂直,且其中一条直线为投影面平行线时,则两直线在该投影面上的投影必定相互垂直。因此,先把AB直线变换成投影面平行线,再作出其垂直平分线即三角形的高线,在高线上定出三角形点C在新投影面上的投影c′1,最后求出点C在H面V面的投影,即可求解。
【作图步骤】
(1)确定X1轴,作新投影轴X1∥ab,把AB换成投影面平行线,得到a′1b′1。
(2)作a′1b′1的中垂线,作X1轴平行线,平行线与X1轴的距离等于c′到X轴的距离,交中垂线得c′1;
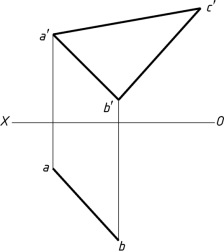
图1-31(a)
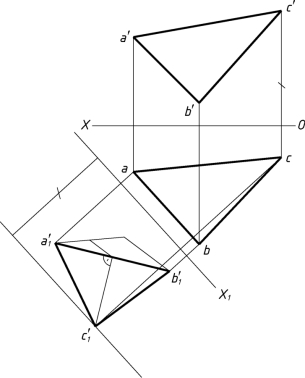
图1-31(b)
(3)最后求出点C在H面和V面的投影即可。答案如图1-31(b)所示。
【问题二十一】 怎样利用换面法求两平面之间夹角?
1-32 用换面法求两平面ABC和BCD之间的夹角。
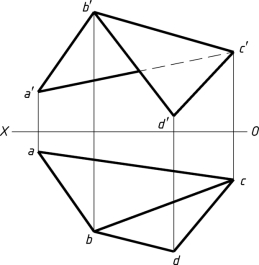
图1-32(a)
【解题分析】
当两平面同时与某一投影面垂直时,则两平面在该投影面上的投影均积聚为一直线,这两条直线之间的夹角就是两平面之间的夹角。对于相交的两平面,把两平面的交线变换成投影面垂直线,使两平面同时与投影面垂直,可以求得两平面间的夹角。
本题中BC为两平面的交线,如果将BC变换成投影面的垂直线,则两平面同时变换为同一投影面的垂直面,即可求得两平面ABC与BDC的夹角。
【作图步骤】
(1)确定X1轴,使新投影轴X1∥bc,把BC换成投影面平行线,得到c′1b′1。
(2)确定X2轴,使新投影轴X2⊥c′1b′1;把BC变换成投影面垂直线,得到b2(c2),则角a2c2b2即为所求。答案如图1-32(b)所示。
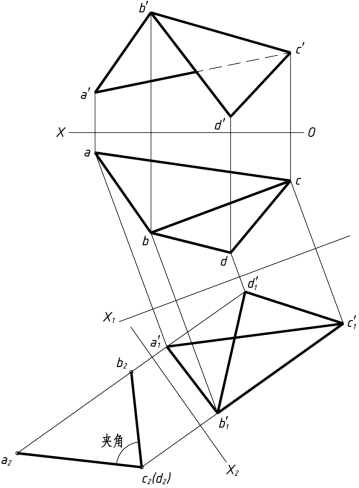
图1-32(b)
1-33 用一段管路KL将EF及GH两段管路连接起来,且KL为最短距离,求KL的投影。
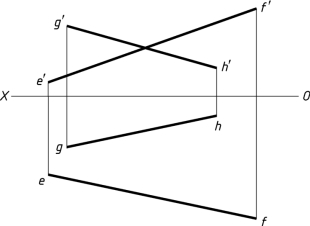
图1-33(a)
【解题分析】
当将其中一条直线变换为两条交叉直线之间的最短距离KL,并为其共垂线与它们交点的连线投影面垂直线时,则KL为该平面的平行线。
【作图步骤】
(1)将直线EF经过两次变换成为投影面垂直线时,直线GH也随之一起变换,EF、GH经两次变换后在H2面上的投影分别为e2f2、g2h2。
(2)假设K为共垂线与EF的交点,L为共垂线与GH的交点,则e2(f2)点即为k2点,过k2作直线垂直g2k2交点即为l2,k2l2反映EF、EH两直线间的距离。
(3)因L属于GH得l′1,过l′1作平行于O2X2直线交e′1f′1得k′1(关键点)。
(4)返回求出k1,k′1。
答案如图1-33(b)所示。
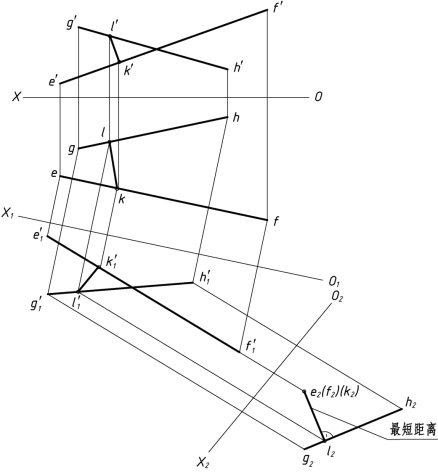
图1-33(b)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




