抗裂验算是针对使用上要求不允许出现裂缝的构件进行的验算。例如，简支的矩形截面输水渡槽底板在纵向弯矩作用下，因底板位于受拉区，一旦开裂，裂缝就会贯穿底板截面造成漏水，因此底板在纵向计算时属严格要求抗裂的构件，应按抗裂条件进行验算。受弯构件抗裂验算以受拉区混凝土将裂未裂的极限状态为依据。
1.抗裂极限状态
由试验得知，受弯构件正截面在即将开裂的瞬间，其应力状态处于第Ⅰ应力阶段的末尾。此时，受拉区边缘的拉应变达到混凝土的极限拉应变εtmax，受拉区应力分布为曲线形，具有明显的塑性特性，最大拉应力达到混凝土的抗拉强度。而受压区混凝土仍接近于弹性工作状态，其应力分布图形为三角形[图2-13（a）]。
2.开裂弯矩Mcr
根据试验结果，在计算受弯构件的开裂弯矩Mcr时，可假定混凝土受拉区应力分布为梯形，塑化区高度占受拉区高度的一半，如图2-47所示。
图2-47 受弯构件正截面即将开裂时的假定应力图形
利用平截面假定，可求出混凝土边缘应力与受压区高度之间的关系。然后根据力和力矩的平衡条件，求出截面开裂弯矩Mcr。
但上述方法比较繁琐，为了计算方便，采用等效换算的方法，即在保持开裂弯矩相等的条件下，将受拉区梯形应力图形等效折算成直线分布的应力图形，如图2-48所示。此时，受拉区边缘应力由ft折算为γmft，γm称为截面抵抗矩的塑性系数。
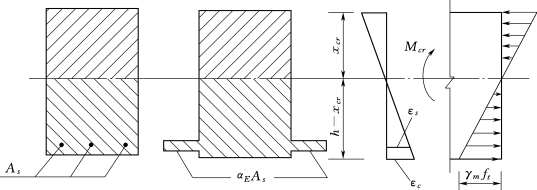
图2-48 受弯构件正截面抗裂弯矩计算图形
经过这样的换算，就可以把构件视作截面面积为
的均质弹性体，引用工程力学公式，得出受弯构件正截面开裂弯矩的计算公式为
式中 W0——换算截面受拉边缘的弹性抵抗矩，mm3；
y0——换算截面重心至受压边缘的距离，mm；
I0——换算截面对其重心轴的惯性矩，mm4；
γm——截面抵抗矩的塑性系数，见表2-7。
表2-7 截面抵抗矩的塑性系数值
注 1.对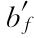
＞bf的工字形截面，可按项次2与项次3之间的数值采用；对于b′f＞bf的工字形截面，可按项次3与项次4之间的数值采用。
2.根据h值的不同，表内数值尚应乘以（0.7+300/h），0.7+300/h的值应不大于1.1，式中h以mm计，当h＞300mm时，取h=300mm，对于圆形和环形截面，h即外径d。
3.对于箱形截面，表中值是指各肋宽度的总和。
3.抗裂验算公式(www.xing528.com)
为满足目标可靠指标的要求，对受弯构件同样引入拉应力限制系数αct，荷载和材料强度均取用标准值。这样，受弯构件在荷载效应的标准组合下，应按下列公式进行抗裂验算，即
式中 Mk——按荷载标准值计算的弯矩值，kN·m；
αct——混凝土拉应力限制系数，对荷载效应的标准组合，αct可取0.85；
ftk——混凝土抗拉强度标准值，N/mm2。
图2-49 双筋工字形截面
4.换算截面的特征值
在抗裂验算时，需先计算换算截面的特征值。下面列出双筋工字形截面的具体公式。对于矩形及T形或倒T形截面，只需在工字形截面的基础上去掉无关的项即可（图2-49）。
换算截面面积为
换算截面重心至受压边缘的距离为
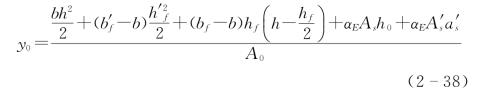
换算截面对其重心轴的惯性矩为
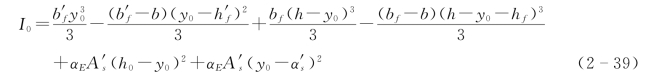
单筋矩形截面的y0及I0也可按下列近似公式计算，即
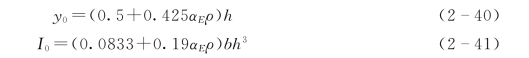
式中 αE——弹性模量比，αE=Es/Ec；
ρ——纵向受拉钢筋的配筋率，ρ=As/（bh0）。
5.提高构件抗裂能力的措施
在混凝土即将开裂时，钢筋的拉应力是很低的。用增加钢筋的办法提高构件的抗裂能力是不经济、不合理的。提高构件抗裂能力的主要方法是加大构件截面尺寸、提高混凝土的强度等级、在混凝土中掺入钢纤维或采用预应力混凝土结构。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
